概要
今回の記事に関しては以下の記事をほぼそのまま参考にさせてもらっています。
実装自体はUnityで行い、コードもC#で作りましたがベースとなる理論は記事をそのまま参考にさせていただきました。
マルペケさんの記事には毎度本当にお世話になっています。
ここでは、そこで得た知識を「自分なりに」理解した内容をまとめて解説したいと思います。
ちなみに今回の記事を書くのに、Unityで実装したサンプルがあります。(サンプルプロジェクトはGithubに上げてあります)
実行イメージは以下のようになります。
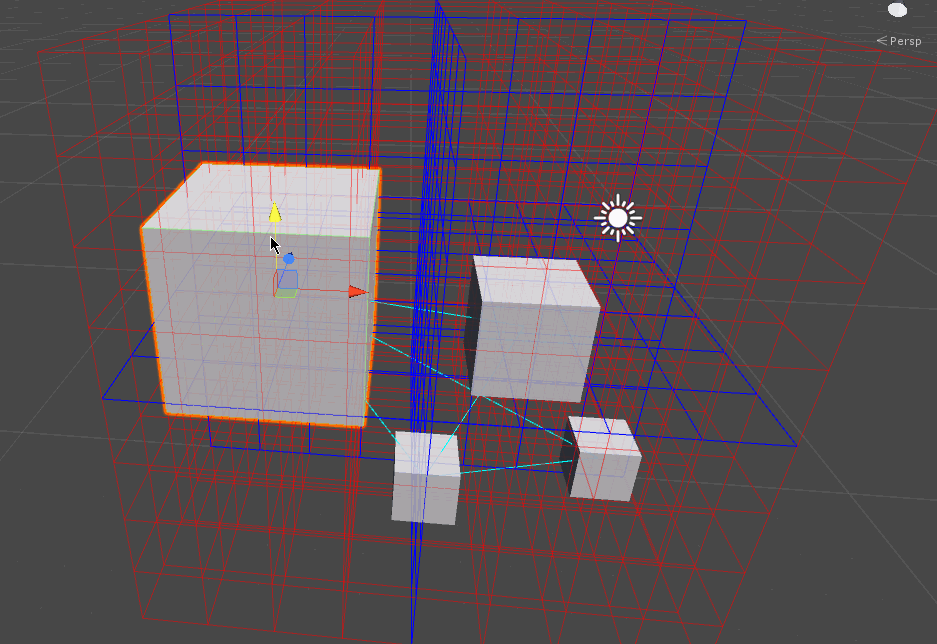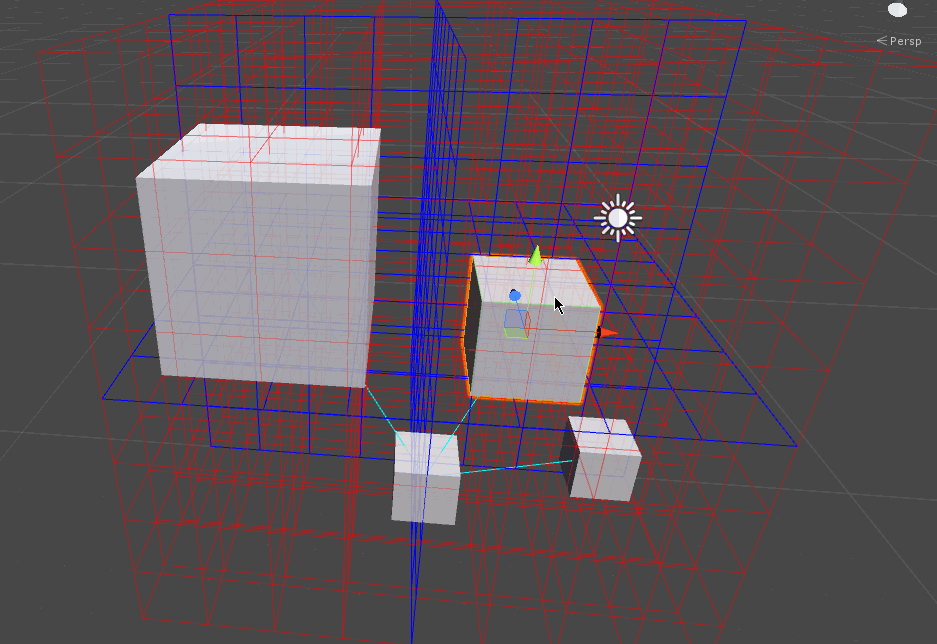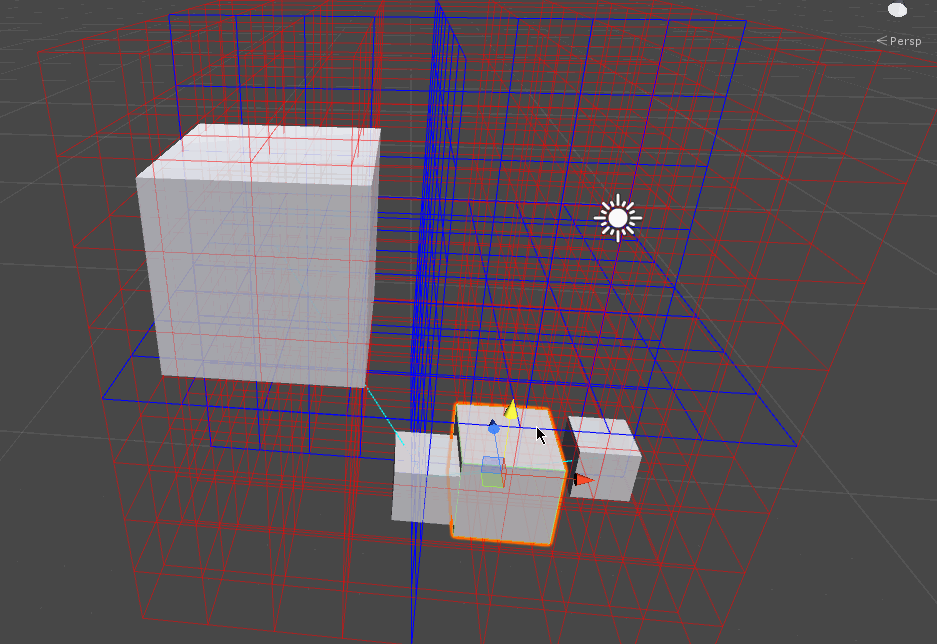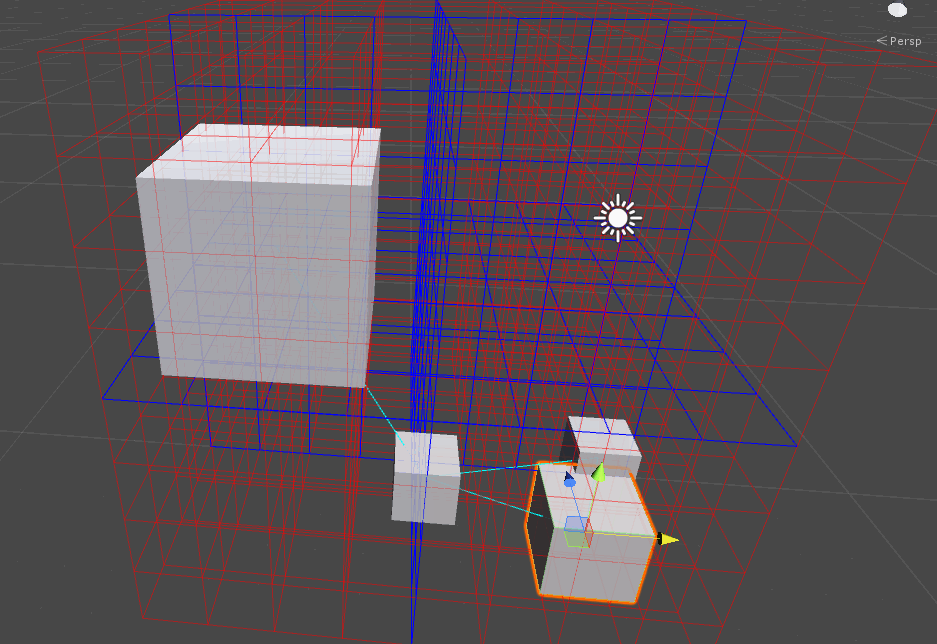
赤いラインがセルを表現していて、どの空間に所属しているかによって衝突可能性のあるオブジェクト同士をラインで結ぶというデモです。
参考にさせていただいた記事
そしてこれを使って実際にUnity上で動くサンプルも作ってみたので、興味がある方は見てみてください。
https://github.com/edom18/MortonOrder
ちなみにどんな内容かと言うと、八分木(Octree(オクトツリー))という概念を使って、3D空間を格子状に分割し、衝突判定などを効率的に行うための理論です。
Wikipeidaから引用させてもらうと以下のようなイメージです。

八分木(オクトツリー)とは
八分木(英: Octree)とは、木構造の一種で、各ノードに最大8個の子ノードがある。3次元空間を8つのオクタント(八分空間)に再帰的に分割する場合によく使われる。四分木を3次元に拡張したものと見ることができる。英語の名称は oct + tree に由来するが "octtree" とは書かず "octree" と書く。
Wikipediaから引用
図を見てもらうと分かりますが、ひとつのBoxが8つに分割され、さらにその分割されたうちのひとつのBoxがまた8つに分割されていく、という構図になっています。
そしてこれを理解する上で重要なポイントは、2進数で考えること。
8つなので3bit単位で分割されていくわけですね。
以下からの解説に関してはこのbitを意識して読んでもらうと分かりやすいかと思います。
※ ただし、今回の記事のほぼすべての解説は2D平面による解説(4分木)となっています。(なので2bit単位)
が、基本的にX,Y軸に加えてZ軸を追加するだけで、基本的な考え方はあまり違いはありません。
モートンオーダー(モートン順序)
これ、最初に知ったときは驚きました。
空間に登録するための判定処理が、まさかオーダーO(1)にまで縮小できるなんてと。
世の中にはほんとに頭のいい人がいるんだなーと思わされました。
2進数(2bit)で空間を分解していく
まずは以下の図を見てください。
4つごとにどんどん分割されていく状況を示しています。

じーっと図を見ていると、徐々になにかが見えてきます。
冒頭で話した通り、それは「2進数」です。
ひとつの空間を4つに分割する。つまり2進数で言うと2桁ですね。コンピュータなら2bit単位です。
そしてそれをひとつの単位として、さらにそれを分割する場合は、また2bitで分解します。
つまり、ひとつ下のレベルに分解するに従って末尾に2bitずつ追加されていく、と見ることもできます。
上の図をベースに説明すると、ルート空間は当然ながら「0」ですね。これは分割してないので当然です。
これをひとまず2bitを使って00と表現しておきます。
さてでは次に。これを4分割します。すると2bitなので2桁の2進数を末尾に追加します。
すると合計4桁になるので00 00となりますね。
そして下位2bitは当然、0〜3の値を持つことができます。まさに分割された空間のindexですね。
ではさらに続けて、それを分解してみましょう。すると、00 00 00と6桁になります。
末尾2桁は前述と同じく0〜3となります。
つまり、親空間を示すのが(上記の例で言えば)中央の2bitに当たります。
以後は、親→子→孫→ひ孫と分解レベルが上っていくにつれて末尾にたされる2bitもそれに応じて増えていくことになります。
しかし今見たように、基本的なルールはなにも変わりません。
試しに45番を例にしていましょう。
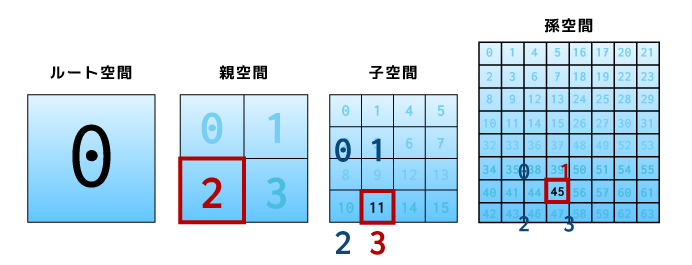
まず、孫での45番は一番右の図の位置になります。
そして左にいくに連れて親空間での位置になります。
45という数字を2bit単位に分解して考えると、確かにそれぞれの空間のindexが隠れていることが分かるかと思います。
(ルート空間は0なので省略)

前述の説明を借りるなら、親空間の2、つまり10を分解して2bitを末尾に足し、さらにそのindexである3、つまり11を追加。
さらにそれを分割して1(01)を末尾に追加し、これを10進数に戻せば45が出て来る、というわけですね。
こう考えるとなんとなく数値と分割の関連が見えてこないでしょうか。
裏を返せば、示された番号を2進数に分解して、かつ2bit単位で分けていくと各空間のindexが顔出す、というわけです。
別の言い方をするなら、2進数の概念を整理してうまく視覚化したもの、と見ることができるかもしれません。
最初にこれを見たときはまさにこの感覚を持ちました。
つまり、空間の通しindex番号をひとつ与えられただけで、そのオブジェクトがどの空間のどの位置にいるか、ただのビットシフトのみで計算できるというわけなのです。
計算量として表せばO(1)のオーダーとなります。なんとすばらしい! 真面目にどの位置にいるか線形検索していては到底たどり着けない高速さです。
座標位置から、所属する空間番号を割り出す
空間分割をモートンオーダーで行うと、すばらしく簡単に空間番号を割り出すことができることが分かりました。
では実際に利用するシーンを仮定して見てみましょう。
以下の図を見てください。

空間分割している意味は、そもそも動くオブジェクトとのあたり判定など「総当り」で調べることをせず、簡単に「近くの」オブジェクトを探すことが目的です。
なので「このオブジェクトはどこに属しているのか?」を知ったり、「この点の近くにあるオブジェクトは?」といったことにも答えられなければなりません。
しかしそれもとても簡単に達成することができます。
上記の図は、孫空間まで分割された状態(8x8=64分割)を示しています。
仮にルート空間の一辺の長さを100とした場合、孫空間での単位距離は8({=2^3})で割ることで求められます。
そして(例えばユーザがクリックした位置などとして)35, 58という座標が与えられたとしましょう。
これを、求めた単位距離で割ると2.8, 4.64となります。そしてこれをさらに端数切り捨てて2, 4にします。
これは、64分割された空間の左から2番目、上から4番目の位置であることを示しています。(indexなので0番始まりな点に注意)
つまり「36」の位置になります。
さて、今までずっと2進数で話をしてきたので、こちらも同じく2進数で見比べてみましょう。
すると、最初の2, 4は010, 100となります。
そして「36」を2進数で表すと100100となります。
ちなみに上では3bit単位で表現していますが、これは空間の分割回数(空間レベル)からです。(冒頭で書いた2D = 2bit、3D = 3bitの意味ではありません)
今回の例では3回分割を行っているため3bit表現になっています。空間分割が2進数の視覚化と考えれば、分割数がそのままbitとして出現するのはイメージができるかと思います。
実はこれ、2bit単位で見たときにxの値(=2)を右のbit、yの値(=4)を左のbitとして合成すると、100100となるのです。
|_0|_1|_0| // xの値は2bit単位で区切った際の右bit |1_|0_|0_| // yの値は2bit単位で区切った際の左bit ---------- 10 01 00
なんということでしょう。
xの値は右のbit、yの値は左のbitとして機能しているわけですね。
そしてこれは、これに限らずすべての空間について成り立ちます。
前述のように、この数値から孫空間だけでなく、子空間、親空間のどの位置か、までが一発で決まってしまいます。やってみましょう。
まず、100100を2bit単位に分解します。すると、10 01 00と分けることができます。
左から順に、「親空間」「子空間」「孫空間」の位置を表していたのでしたね。
親空間は10です。つまり、2番の位置にあることがわかります。図にすると以下ですね。

孫空間の36番は確かに「親空間」の2番の位置にあるのが確認できます。
では「子空間」ではどうでしょうか。
子空間の番号は01、つまり1ですね。1は右上です。図で言うと、

こちらも確かに1番の位置にありました。
最後は孫空間です。
孫空間は00ですね。つまり0、左上です。

こちらも確かに左上にありました。
以上のように、bit演算だけで、座標からびしっと空間を特定する方法、それが「モートンオーダー」です。
これを考えた人、ほんと天才だと思います。
以上を踏まえた上で、x,yの値から孫空間の位置を割り出す関数(bitシフト)は以下のようになります。
int BitSeparate(n) { n = (n | n << 8) & 0x00ff00ff; n = (n | n << 4) & 0x0f0f0f0f; n = (n | n << 2) & 0x33333333; return (n | n << 1) & 0x55555555; }
「オブジェクト」の所属空間を求める
さて、前述のように「点」がどの位置にあるかを求める方法が分かりました。
しかし、ほとんどの場合、オブジェクトは点ではなく、ある程度の大きさを持った「ボリューム」となります。
そしてそのサイズによっては孫空間には収まらず、「どの空間分割数が適切か」を判断しないとなりません。
2Dの場合、大きさを考慮するには左上と右下の値を採用し、いわゆるAABB(軸並行バウンディングボックス)で考えることで解決できます。

つまり、左上の点と右下の点ふたつの所属空間をまず求め、その後にそのサイズに応じてどの空間に属するかを判断します。
とはいえこれは簡単ではありません。― 普通に考えては。
これまたすごい発想(というかどうしたらそんな発想が出るのかと思ってしまいますが)を利用します。
参考にさせていただいた記事から引用させてもらうと、
上の例だと左上は19番、右下は31番に含まれています。ここからが面白いところで、色々と試行錯誤し、またJagoon様からのご指摘によって修正されたうれしい法則です。右下の空間番号31と左上空間番号19の排他的論理和を取ると12となります。この12を2進数で表現するとこうなります:
実は、境界図形の所属する分割レベルはこの排他的論理和の結果ビットが0じゃない最上位の区切りに表現されます。上の例だと青色で示した区切りが[11]となっています。所属空間は、上の例のように一番下の区切りを一つ上のレベル(ここでは子になります)、そこから親、ルートと空間レベルを上げていきます。[11]のビットはこの法則に従うと「親空間に所属」と判断されます。
とのこと。ほんとbit演算さまさまです。
サイズに応じてどの空間に属するか、ほぼO(1)で処理が済んでしまいます。
XORでなぜ所属空間が求まる?
このXORで出てくる理由。自分の理解を添えておくと、以下のようなイメージです。
各番号には所属親空間の情報が残っている。つまり、同じ親空間の情報はXORで取り除かれる。
結果として、違う親空間にいる場合はそれが「フラグ」として抽出される。
という感じです。
ここで「フラグ」と書いたのは、抽出した値自体に意味はなく、「どの位置のbitが立っているか」という、まさにフラグ的な利用をするからです。
その利用については後述します。
試しにひとつ例題をやってみましょう。
以下の図を見てください。

左上を32、右下を47とします。まず、図を見て答えを見つけてしまうと「親空間」の2に所属することが分かりますね。これを計算で求めてみましょう。
32^46 = 15となります。2進数にすると1111ですね。4分割なので00 11 11と3つ分で表します。(子空間から始めるので4-1 = 3)
そして「ルート 親 子」のどこに属しているかは、bitが立っている位置を参考にします。
具体的には「どの位置のbitが立っているか」です。
上記の例で言うと、3つに分解した範囲で考えると、左から2つめ、および3つめにbitが立っていますね。
そしてbitが立っている部分の、一番左側を採用します。
「ルート/親/子」の3つとして考えると「親」の部分のbitが一番左側のbitとなります。
つまり所属空間は「親」ということになりますね。
こうして手作業で探すのは簡単ですが、プログラムでもそれほどむずかしくはありません。
2bit単位で見ているだけなので、最初の2bitをチェックして値が1以上かをチェックし、そうであった場合に空間レベルを上げていく、というふうに実装すればよいのです。
実際に今回これを実装した箇所は以下のようになります。
(ちなみに下のコードでは3Dに拡張しているため、3bitごとチェックしている点に注意してください)
int xor = ltd ^ rbd; // 2点の位置のXOR int i = 0; int shift = 0; int spaceIndex = 0; while (xor != 0) { // 下位3bitずつマスクして値をチェックする if ((xor & 0x7) != 0) { // 空間シフト数を採用 spaceIndex = (i + 1); shift = spaceIndex * 3; } // 3bitシフトさせて再チェック xor >>= 3; i++; }
計算結果の下位3bitの値をチェックし、0以外=bitが立っているので、その場合はいったんその空間レベルを記憶しておきます。
そして計算結果を3bitシフトして再チェック。以後、値が0になるまでこれを繰り返し、最終的に得られた結果が空間レベルと、空間レベルを得るために必要なシフト数が得られる、というわけです。
さて、実際にこれを前述のルールの沿って見てみると、親空間のindexを得るには右4シフトすればいいことが分かります。
なぜか?
そもそも求めた番号には常に、その親に当たる空間のindexは含まれているのでしたね。
なので、「どの親に所属するか」さえわかれば、あとは数値をその親空間までシフトしてやれば自然とそのindexが姿を表す、というわけです。
実際にやってみましょう。
右下の数字47を右に4シフトすると(47 >> 4)答えは2です。
(ちなみに、どちらも同じ親に属しているので、32のほうを4bit分シフトしても同じ値が算出できます)
つまりまとめると「親空間の2に属する」となりました。
図で見ていた通りの結果になりましたね。すごい!

線形4分木でアクセスを高速化
前述の話は、すべてツリー状(木構造)での話でした。
しかしそれでは再帰的に調べていなかければならず、せっかく空間への登録・確認がO(1)にできたのに意味がなくなってしまいます。
これもO(1)で取れるようにしてみましょう。
今まで出てきたものを線形、つまりひとつの配列に収めてしまいます。

上図のように、線形配列に直したものを線形4分木(Liner Quaternary Tree)と呼びます。
線形の配列(リスト)にすることで、これまた各空間へのアクセスをO(1)にします。
ただ当然ですが、各分割レベルの最初のindexは0です。
そのまま分割空間レベルごとのindexを使うわけにはいきません。
以下のように通し番号として表現する必要があります。
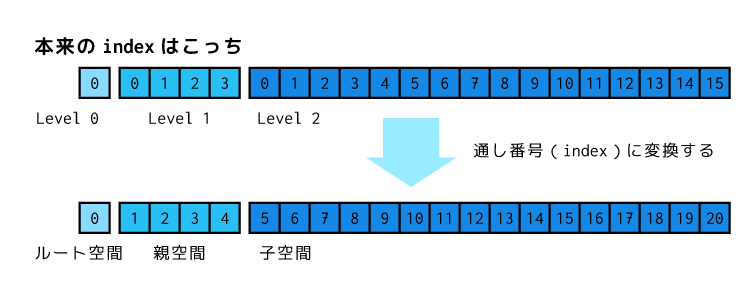
図を見てもらうと分かりますが、各分割空間レベルの最初のindexはその前の空間レベルの分割数の合計を足した数になっているのが分かるかと思います。
例えばレベル2なら、その前にはルート空間で1、その下の空間で4、合計5個の要素があります。
なのでレベル2は5から始まっているわけですね。
そしてこれを計算するには「等比級数の和」を利用し、以下のように式で表すことができます。
\( 足す数 = \frac{4^L - 1}{4 - 1} = \frac{4^L - 1}{3} \)
今回の例では以下のように実装しました。
int ToLinearSpace(int mortonNumber, int level) { int denom = _divisionNumber - 1; int additveNum = (int)((Mathf.Pow(_divisionNumber, level) - 1) / denom); return mortonNumber + additveNum; }
さぁ、これで各オブジェクトの所属空間の検索、更新、登録、操作すべてがO(1)で行えるようになりました。
衝突判定について
衝突判定についても最適化の方法があります。
ただ、今回の記事はあくまで8分木の解説なので、その後のリスト生成などはしません。
参考にしたマルペケさんの記事ではそのあたりについても解説しているので、そちらを参考にしてみてください。
いちおうサンプルとして上げたほうはそれを元に、衝突判定のリストを生成するところまでも実装済みです。
ちなみに衝突判定以外にも、近傍のオブジェクトを取得する、など他にも色々と使いみちはありそうです。
その場合でも、空間へのアクセスがO(1)で行えるので、「近傍」を定義してその空間へアクセスすればすぐにその空間に所属しているオブジェクトのリストを得ることができると思います。
