視錐台とAABBとの交差判定

概要

とあるオブジェクトが「カメラに映る対象か」というのを知りたいケースはあると思います。
また、通常のカメラだけでなく、「視界」を表した視錐台を定義してその中にオブジェクトが含まれるか、というのもあるとありがたい機能でしょう。
（例えば敵AIの視界表現とか）

実際に動かした感じはこんなふうになります↓

視界に入ったら検知、みたいのを作ってみた。ただ、Gizmos.DrawFrustumの範囲が微妙にカメラのそれと違うのはなぜだろう・・。 pic.twitter.com/wd0aY0fzC9
— edom18@AR / MESON (@edo_m18) 2017年10月26日

ただ、ツイートにも書いてますが視錐台を視覚化するGizmosメソッドがありますが、微妙にカメラのそれと違うのが気になりました・・。
気づいた点として、OnDrawGizmosのときのカメラのAspectが、プレイ時のカメラのAspectと違う、というのはありました。

今回の記事、実装は以下の記事を参考にさせてもらいました。

西川善司の3Dゲームファンのための「GRAVITY DAZE」グラフィックス講座（前編） PS Vitaで4倍速半透明描画を行なう秘策と300万ポリゴンのシーンをレンダリングするための裏技とは?

実装したサンプルはGithubにアップしてあります。

考え方

平面には「表面」と「裏面」が存在します。
平面は、平面の位置から表と裏のふたつの空間に分離している、と見ることもできますね。

ここで、「表側」を平面の法線が向いている方向、「裏側」を平面の法線の反対側とし、AABB（Axis-Aligned Bounding Box：軸並行境界ボックス）の8つある頂点のうち、表側の方向にある点の中で一番端の点を「Positive Point（正の頂点）」、裏側の方向にある点の中で一番端にある点を「Negative Point（負の頂点）」とします。

そしてそれら2頂点の平面との距離を測り、その結果によって平面のどちら側にAABBが存在しているか（あるいは交差しているか）を判定します。

と、言葉だけでは分かりづらいと思うので、図にすると以下のようになります。

図解すると以下のようになります。

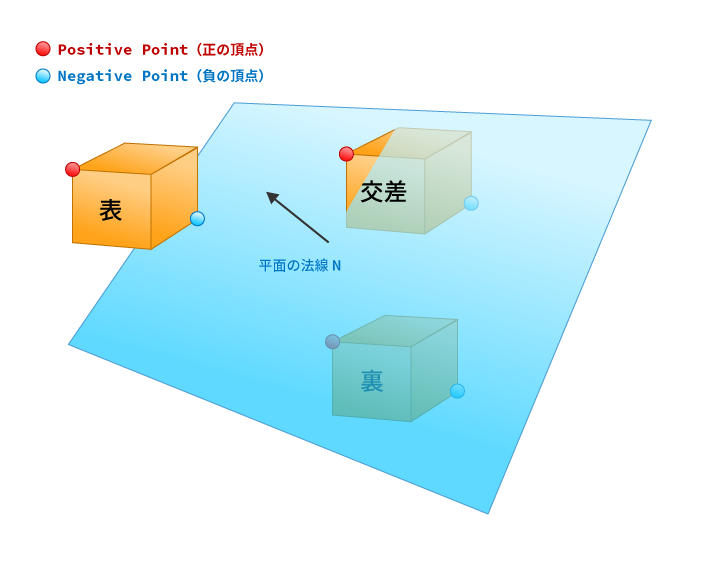
AABBの位置の判定方法

AABBの位置の判定方法ですが、意外にシンプルです。

まず、定義した正の頂点と平面との垂線の距離を測ります。
仮にその距離（内積結果）がマイナスだった場合、これは正の頂点が裏側にあることになります。

上記の図を見てもらうと一目瞭然ですが、正の頂点がそもそも裏側にある場合、AABBは必ず裏側にあることになります。

さて、正の頂点がプラス側にある場合、AABBは平面の表側に存在することが確定します。
しかし、状況として以下の2点が考えられます。

AABBが完全に表側にある
AABBが平面と交差している

もし交差を無視していいのであれば、この時点で判定は終わりになりますが、交差も求めたい場合はさらに計算を続けます。
といっても計算は正の頂点に行ったものと同じことを、負の頂点にも行うだけです。

もし、負の頂点と平面との垂線の距離がプラスだった場合は、AABBは完全に平面の表側にあります。
逆に、距離がマイナスだった場合は、負の頂点が平面の裏側にあることになるので、AABBは平面と交差していることになります。

AABBと平面との判定がこんなに簡単にできるのは驚きですね。

視錐台の内外を判定する

以上で、平面とAABBの交差判定が行えることが分かりました。
今回は、カメラの視錐台にオブジェクトが入っているかどうか、の判断を行いたいため、これだけでは終わりません。

といってもほぼ答えは出ている状態です。

つまり、視錐台は6つの平面で出来ている、と考えることができるので、この6平面との交差判定を行い、そのすべての平面と交差、あるいは表側にある、と判定されれば、それは視錐台の中にオブジェクトが含まれている、と考えることができるのです。

考え方は以上で終わりです。理論としてはとてもシンプルですね。
以下からは、それらの計算方法について詳しく見ていきたいと思います。

正・負の頂点を求める

AABBが持つ8頂点のうち、どの点が平面に対して正の頂点・負の頂点となるのか。
その取得には面の法線のみで決定することができます。

実際に実装した内容は以下のようになります。

/// 
/// 法線から一番近い点を算出する
/// 
/// ターゲットとなるAABB
/// 算出する法線
/// 
static private Vector3 GetPositivePoint(Collider target, Vector3 normal)
{
    Bounds bounds = target.bounds;
    Vector3 result = bounds.min;

    if (normal.x > 0)
    {
        result.x += bounds.size.x;
    }
    if (normal.y > 0)
    {
        result.y += bounds.size.y;
    }
    if (normal.z > 0)
    {
        result.z += bounds.size.z;
    }

    return result;
}

/// 
/// 法線から一番遠い点を算出する
/// 
/// ターゲットとなるAABB
/// 算出する法線
/// 
static private Vector3 GetNegativePoint(Collider target, Vector3 normal)
{
    Bounds bounds = target.bounds;
    Vector3 result = bounds.min;

    if (normal.x < 0)
    {
        result.x += bounds.size.x;
    }
    if (normal.y < 0)
    {
        result.y += bounds.size.y;
    }
    if (normal.z < 0)
    {
        result.z += bounds.size.z;
    }

    return result;
}

処理はとてもシンプルです。

渡された面の法線ベクトルの各成分のプラス・マイナスを見て、プラス（マイナス）側に属する点を算出しているだけです。
なので、法線ベクトルの各成分の0未満、0より上かの判定だけで点の位置を求めています。

なぜ法線だけで求まる？

なぜこれだけで点が求まるのか。
理由は、AABBは「座標に対してすべての辺が垂直・平行である」ということを考えれば分かります。

例えば、平面の法線の方向が上に向いている（Y軸の値がプラス）の場合、AABBの正の側の頂点は必ず上部にある点に限定されます。
あとはこれを、XZ軸に対してもそれぞれ行ってやれば、めでたく正・負の頂点が求まる、というわけです。

さぁ、ふたつの点が算出できたので、次は平面との距離の計算に進みましょう。

平面との距離を計算する

平面との交差判定のために、平面に対する垂線の距離が必要となります。
平面と頂点の垂線の距離は、平面の法線との内積を取ることで簡単に計算することができます。
具体的には、距離を測りたい点Aと、平面の位置を表す点Bとのベクトル「 $\vec{AP}$ 」と平面の法線「 $\vec{N}$ 」との内積の絶対値が垂線の長さとなります。

図にすると以下のようになります。

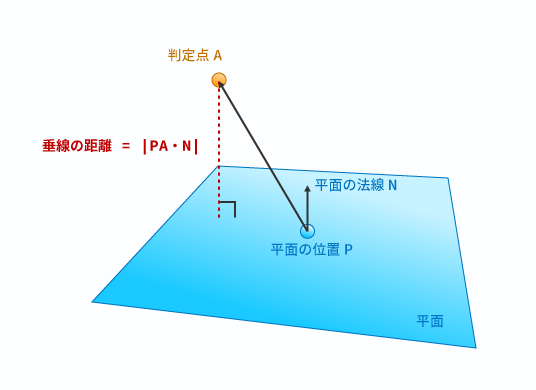
ただし、今回は「表」をプラス、「裏」をマイナスとするため絶対値ではなくそのまま結果を利用することで、表裏の判定も含めて距離を算出することができます。

視錐台の6平面の法線を求める

さて最後は、問題となる視錐台を構成する6平面の、各平面の法線の求め方です。
求め方は以下の記事がとても分かりやすく書かれています。

http://miffysora.wikidot.com/frustum-extract-plane

まず考え方として、判定したい点 $v$ にProjectionMatrix（射影行列）を掛ます。

ProjectionMatrixを $P$ とし、判定したい頂点を $v$ とすると、

と書けます。

行列とベクトルの掛け算は行とベクトルとの内積を計算するのと同じことなので、以下のように書くことができます。

このとき、変換された $v'$ は「同次座標」と呼ばれ、これは「クリッピング座標系」となります。
（ $w$ で全要素（ $x, y, z$ を割ることで、クリッピング座標系は立方体となります）

参考: http://miffysora.wikidot.com/clip-coordinates

さてここで、以下の式を満たすとき、 $x$ は視錐台の中に収まります。

つまり、すべての要素に対して不等式が成り立てば、頂点 $v$ は視錐台内にある、と判定されます。

そしてそれぞれの不等式の意味は以下のようになります。

(1) ... x'は視錐台の左平面の内側
(2)... x'は視錐台の右平面の内側
(3) ... y'は視錐台の下平面の内側
(4)... y'は視錐台の上平面の内側
(5) ... z'は視錐台の近平面の内側
(6)... z'は視錐台の遠平面の内側

ここで、左平面に着目してみると、

を満たすとき、点 $x$ は左平面の「表側」にいることになります。

この式は以下から得られます。

として得られます。展開すると、

となります。

さらに整理して、

となります。

$v$ は $(x, y, z, w)$ です。上記は、ベクトルのそれぞれの成分と、行列の成分（ $row_4 + row_1$ ）を足したものの内積を取る、ということになります。

つまり、

$w$ の値は常に1で消せるので、

となります。

（ $x$ 成分に着目すると、 $x * (m_{41} + m_{11})$ ということです）

さてここで、「平面の方程式」を思い出してみます。

mathtrain.jp

平面の方程式は

です。
先程展開した式を見てみるとまさにこの形になっているのが分かるかと思います。

展開した式を平面の方程式に当てはめてみると、

と整理することが出来ます。

そして平面の方程式から、各 $a, b, c$ は平面の法線になります。
（ただし正規化していないので使う際に正規化する必要あり）

あとは、それぞれの平面に対して上記を求めてやれば視錐台の6平面の法線が求まります。

平面	係数a	係数b	係数c	係数d
左	m41 + m11	m42 + m12	m43 + m13	m44 + m14
右	m41 - m11	m42 - m12	m43 - m13	m44 - m14
下	m41 + m21	m42 + m22	m43 + m23	m44 + m24
上	m41 - m21	m42 - m22	m43 - m23	m44 - m24
近	m41 + m31	m42 + m32	m43 + m33	m44 + m34
遠	m41 - m31	m42 - m32	m43 - m33	m44 - m34

※ ただ、Unityの場合は上記の計算ではうまく行かなかったので、サンプルコードでは若干調整してあります。

いったん整理

ここまでで、以下の道具が揃いました。

射影行列から視錐台の平面の法線の求め方
点と平面の垂線の長さの計算
AABBの正・負の頂点位置の計算

これを元に計算を行えば、カメラのFov、Near、Far、そしてワールド座標位置から射影行列を計算し、さらにその行列から6平面を計算、それぞれの平面に対してAABBが内外どちらにあるかの判定、が行えるようになります。

ちなみに、射影行列の成分の意味についてはマルペケさんのこちらの記事（その70 完全ホワイトボックスなパースペクティブ射影変換行列）が非常に分かりやすいです。

これをゲームに組み込む場合は、毎フレームごとにこれを繰り返してやれば、冒頭の動画のように「視界に入っているか否か」を判定することができるようになります。

注意点として、これはあくまで「射影行列の視錐台の中に入っているか」という判定を行っているにすぎないので、もし視点と対象の間に遮蔽物があったとしても「内外判定」は「true」を返します。
実際のAIに組み込むなどする場合は、さらに視線と対象の間に遮蔽物がないか、の判定が必要になるでしょう。
（ただ、それは今回の解説の範疇外なので割愛します）

サンプルコード

最後に、今回実装したコードを載せておきます。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

static public class CheckFrustum
{
    public enum State
    {
        Outside, Inside, Intersect,
    }

    /// 
    /// 対象AABBとProjection Matrixから視錐台内に入っているかの検知を行う
    /// 
    /// AABB対象
    /// Projection Matrix
    /// カメラ位置
    /// カメラのNear
    /// カメラのFar
    /// 
    static public State Detect(Collider target, Matrix4x4 pmat, Transform eyeTrans, float near, float far)
    {
        Plane[] planes = CalculateFrustumPlanes(pmat, eyeTrans, near, far);

        State result = State.Inside;

        for (int i = 0; i < planes.Length; i++)
        {
            Vector3 normal = planes[i].normal;
            Vector3 vp = GetPositivePoint(target, normal);
            Vector3 vn = GetNegativePoint(target, normal);

            // (vp - plane.pos)・normal
            float dp = planes[i].GetDistanceToPoint(vp);
            if (dp < 0)
            {
                return State.Outside;
            }

            float dn = planes[i].GetDistanceToPoint(vn);
            if (dn < 0)
            {
                result = State.Intersect;
            }
        }

        return result;
    }

    /// 
    /// 法線から一番近い点を算出する
    /// 
    /// ターゲットとなるAABB
    /// 算出する法線
    /// 
    static private Vector3 GetPositivePoint(Collider target, Vector3 normal)
    {
        Bounds bounds = target.bounds;
        Vector3 result = bounds.min;

        if (normal.x > 0)
        {
            result.x += bounds.size.x;
        }
        if (normal.y > 0)
        {
            result.y += bounds.size.y;
        }
        if (normal.z > 0)
        {
            result.z += bounds.size.z;
        }

        return result;
    }

    /// 
    /// 法線から一番遠い点を算出する
    /// 
    /// ターゲットとなるAABB
    /// 算出する法線
    /// 
    static private Vector3 GetNegativePoint(Collider target, Vector3 normal)
    {
        Bounds bounds = target.bounds;
        Vector3 result = bounds.min;

        if (normal.x < 0)
        {
            result.x += bounds.size.x;
        }
        if (normal.y < 0)
        {
            result.y += bounds.size.y;
        }
        if (normal.z < 0)
        {
            result.z += bounds.size.z;
        }

        return result;
    }

    /// 
    /// 指定されたProjection Matricsから視錐台の6面の平面を求める
    /// 
    /// Projection Matrix
    /// カメラ位置
    /// カメラのNear
    /// カメラのFar
    /// 
    static public Plane[] CalculateFrustumPlanes(Matrix4x4 pmat, Transform eyeTrans, float near, float far)
    {
        Plane[] result = new Plane[6];

        // 0: Left, 1: Right, 2: Bottm, 3: Top
        for (int i = 0; i < 4; i++)
        {
            float a, b, c, d;
            int r = i / 2;
            if (i % 2 == 0)
            {
                // 平面の方程式
                // ax + by + cz + d = 0
                a = pmat[3, 0] - pmat[r, 0];
                b = pmat[3, 1] - pmat[r, 1];
                c = pmat[3, 2] - pmat[r, 2];
                d = pmat[3, 3] - pmat[r, 3];
            }
            else
            {
                a = pmat[3, 0] + pmat[r, 0];
                b = pmat[3, 1] + pmat[r, 1];
                c = pmat[3, 2] + pmat[r, 2];
                d = pmat[3, 3] + pmat[r, 3];
            }

            Vector3 normal = -new Vector3(a, b, c).normalized;
            normal = eyeTrans.rotation * normal;

            result[i] = new Plane(normal, eyeTrans.position);
        }

        // for the near plane
        {
            float a = pmat[3, 0] + pmat[2, 0];
            float b = pmat[3, 1] + pmat[2, 1];
            float c = pmat[3, 2] + pmat[2, 2];
            float d = pmat[3, 3] + pmat[2, 3];

            Vector3 normal = -new Vector3(a, b, c).normalized;
            normal = eyeTrans.rotation * normal;

            Vector3 pos = eyeTrans.position + (eyeTrans.forward * near);
            result[4] = new Plane(normal, pos);
        }

        // for the far plane
        {
            float a = pmat[3, 0] - pmat[2, 0];
            float b = pmat[3, 1] - pmat[2, 1];
            float c = pmat[3, 2] - pmat[2, 2];
            float d = pmat[3, 3] - pmat[2, 3];

            Vector3 normal = -new Vector3(a, b, c).normalized;
            normal = eyeTrans.rotation * normal;

            Vector3 pos = eyeTrans.position + (eyeTrans.forward * near) + (eyeTrans.forward * far);
            result[5] = new Plane(normal, pos);
        }

        return result;
    }
}

UnityのAPIを使う

ちなみに、カメラ自体を使う場合はUnityに標準で同等の処理をしてくれるユーティリティがあるので、そちらを使うほうが手っ取り早いでしょう。

// 視錐台の6平面を取得
Plane[] planes = GeometryUtility.CalculateFrustumPlanes(Camera.main);
 
// 内外判定
if (GeometryUtility.TestPlanesAABB(planes, bounds))
{
    // 含まれていたときの処理
}
else
{
    // 含まれていなかったときの処理
}

参考にさせてもらった記事: 【Unity】【数学】視錐台（Frustum）について（第2回） – 株式会社ロジカルビート

docs.unity3d.com