Unityで流体シミュレーションを実装する〜概念編〜

はじめに

今回の実装をするにあたってナビエ・ストークス方程式を解いて実装していく必要があるのですが、正直、数学・物理としての正確な意味の理解や方程式のしっかりとした理解には至ってません。

式の内容やどういうことを行っているのかというのは理解して書いていますが、本当の意味での理解をしたい場合はこの記事は参考にならないかもしれません。

あくまで「プログラムで動かし、実際にインタラクションさせる」という点においての記事になります。

はじめに
概要
ナビエ・ストークス方程式
動画による解説
ナビエ・ストークス方程式の理解
気づいた点や混乱した点のメモ
- 移流項の内積は「発散ではない」
連続の式
- 全微分
ナブラ（の使い方。
演算子の位置について
参考にした記事

概要

今回は流体力学を使った流体シミュレーションを実装したのでその解説をしたいと思います。

内容が濃くなりそうなので概念編と実装編を分けて書きたいと思います。今回は概念編です。

ちなみに実際に動かした動画はこちら↓

前のやつ、ちょっと計算間違っていてちゃんと動いてなかった。直したら見た目もだいぶ自然になった。実装したやつはGitHubにアップしてあるので興味ある方は。これの解説ブログは後日。https://t.co/EprWomMvLv #Unity #Shader pic.twitter.com/wmADqX0Q2T
— edom18@AR / MESON (@edo_m18) 2020年2月9日

だいぶ自然な感じで動いているのが分かるかと思います。

ナビエ・ストークス方程式

さて、流体シミュレーションや流体力学で検索をかけるとこのナビエ・ストークス方程式というのが出てきます。式は以下です。

いきなり見ると「うっ・・・」ってなりますよね。（自分はなりました。でも右辺第一項がちょっとかわいく見えるｗ）

が、これでもかなり簡略化された記述です。これを解き、プログラムで動かすにはどうするか、がこの記事（と次の実装編）の目的となります。

ちなみにそれぞれの項の意味は以下です。

f:id:edo_m18:20200211103647j:plain

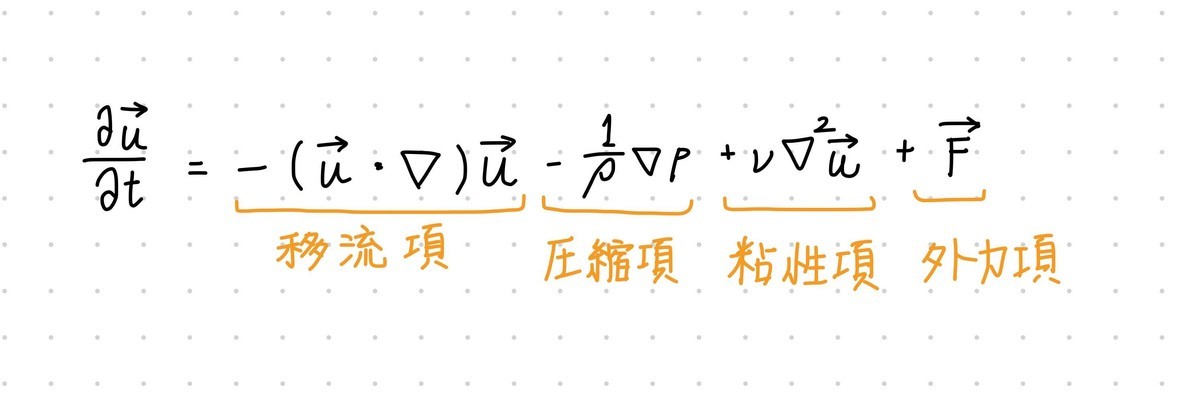
左辺は流体の速度の時間微分を表しています。つまり、流体の速度変化を求める式が右辺ということになります。

各項ごとに説明をつけましたが、これはつまり「流体の時間微分（＝速度変化）」は「移流」「圧縮」「粘性」「外力」の合成として求めることができる、というのがこの式の言いたいことです。

動画による解説

上記の各項について、そもそもなぜ流体の速度変化がこの式で求まるのでしょうか。
その答えは、つまり各項の導出は以下の動画を見ると分かりやすいと思います。図と式を用いてとても分かりやすく解説してくれています。
（~~自分で説明できるほど理解してないから丸投げ~~）

www.youtube.com

動画の冒頭でだいたい小さいボケをするんですが、個人的にはとても好きですｗ

ナビエ・ストークス方程式の理解

導出や各項の意味については上記動画をご覧ください。
ここでは、理解を深めるために方程式の各項を別の視点から見てみたいと思います。

実はナビエ・ストークス方程式は流体力学における運動方程式です。
形は複雑になっていますが、古典力学同様 $F = ma$ の形になっているのです。

こちらの記事ではまた少し異なる形の式が示されています。

ここで、それぞれをニュートン力学に当てはめると「 $ρ$ 」が「 $m$ 」、「 $\frac{\partial \vec{u}}{\partial t} + (\vec{u} \cdot \nabla)\vec{u}$ 」が「 $a$ 」、「 $-\nabla p + μ\nabla^2 \vec{u} + ρ\vec{F}$ 」が「 $f$ 」と考えることができます。

こう見ると少しだけ簡単な気がしてきますね。（錯覚）

未知数と式の数

さて、実は冒頭の式だけではこれを解くことができません。
理由は、未知数が4つに対して式が3つしかないためです。式がひとつ足りないんですね。

そこで、一般的な流体の持つ非圧縮性という性質を利用してもうひとつ式を作ります。

非圧縮性を利用する

非圧縮性とは、とある流体が場所によらず一定で圧縮されないという意味です。
イレギュラーっぽい感じがしますが、実は水や空気など、身の回りにあるものはほぼ非圧縮性があるそうです。
動画でそのあたりにも言及されていました。

さてこの非圧縮性を導入するとなぜ解けるのか。
その理由は、非圧縮性を表す式として以下の式を定義することができるためです。

これが意味するところは流体の速度の発散が0になることを意味しています。

「発散」がどういう意味かというと、観測のとある地点において「プラスであれば湧き出し」、「マイナスであれば吸収」となります。
しかし水などの通常の流体は突然その状態が変わることはなく、とある地点から別の地点に移動した分の質量は、別の地点にあった同量分、さらに別の場所に押し出されるため常に密度は一定に保たれます。これが「非圧縮性」ってことなんですね。

つまり、流体の各地点において発散がゼロ＝流入も流出も釣り合っている状態＝圧縮されていない状態＝非圧縮性、ということを意味しているわけです。

この式を加えることで「未知数が4つ」「式が4つ」になるのでこれを連立して解くことができるようになります。

なお、冒頭の動画で話されていますが、現時点ではこの方程式の一般解は説かれておらず、解ければ100万ドルがもらえる懸賞問題となっているようです。（そもそも一般解が存在するかも分かっていないらしい）

実際には数値解析によって流体を表現します。

移流項の計算

移流項は、プログラムでは該当位置の速度分後ろに進んだ位置の速度を自身の速度として利用することで達成します。詳細は後編の実装編を確認ください。

ちなみに式は $-(\vec{u} \cdot \nabla)\vec{u}$ となっていることから、今の速度の微小量分前（マイナス）の値を使うというのがなんとなく想像できるかと思います。

粘性項

実は今回の実装では粘性項は計算していません。ざっくりと毎フレーム0.99などの値を乗算して辻褄を合わせています。

こちらの記事では粘性項についても触れられているので参考になるかもしれません。

blog.livedoor.jp

外力項

外力項は任意の値です。というのも、通常流体はなにもしなければ動きません。
静かな水面を見ているとほぼ動いていないのが分かるかと思います。

つまりこの外力項は「流体をどう動かしたいか」を表します。
なのでなにもしなければ常にゼロです。

今回はマウスをドラッグした際にそれを速度として扱い、対象の点（マウスの位置の点）にマウスの速度を加えて計算しています。

圧力項の計算 - ポアソン方程式

さて最後が圧力項です。これを最後に持ってきたのは、この計算が一番要になるからです。

色々資料を漁っていると、圧力に対する解法としてポアソン方程式が出てきます。
ポアソン方程式については以下の記事が分かりやすかったです。

teamcoil.sp.u-tokai.ac.jp

記事から引用させてもらうと、

電荷が無い場合のPoissonの方程式(Laplaceの方程式)の意味するところは，「ある場所の電位は，近傍の電位の平均値に等しい」と言っているに過ぎないことに気がついただろうか．

と書かれています。
そして記事に書かれている式を引用させてもらうと以下の式が最後に紹介されている式になります。

上記記事が解説している式をプログラム的に解くと、以下のように、計算したいピクセル位置の近傍、上下左右をサンプリングして計算を行うことが出来ます。
（後編で紹介する実際に実装したコードから抜粋）

float3 px = float3(1.0 / w, 1.0 / h, 0);
float2 uv = float2(id.x / w, id.y / h) + px.xy * 0.5;

float x0 = _SourcePressure.SampleLevel(_LinearClamp, uv - px.xz, 0).r;
float x1 = _SourcePressure.SampleLevel(_LinearClamp, uv + px.xz, 0).r;
float y0 = _SourcePressure.SampleLevel(_LinearClamp, uv - px.zy, 0).r;
float y1 = _SourcePressure.SampleLevel(_LinearClamp, uv + px.zy, 0).r;

float d = _ResultDivergence[id].r;
float relaxed = (x0 + x1 + y0 + y1 - d) * 0.25;

x0 + x1 + y0 + y1の部分が上下左右の近傍の値を足しているところですね。そして上記式の最初の項がdに該当するのだと思います。
（すみません、このあたりは理解が浅いです）
そして最後に0.25（= $\frac{1}{4}$ ）を掛けています。

ポアソン方程式をヤコビ法を使って解く

実際のプログラムではこれを複数回実行して近似値を求めています。（これをヤコビ法と言います）

ヤコビ法についてはこちらのPDFが分かりやすかったです。

例を引用させてもらうと以下のようになります。

1.1 ヤコビ法
例 1. 方程式

が与えられたとき, 各方程式を各々の変数について解き

$x^{(0)}, y^{(0)}, z^{(0)}$ を適当に決めて（例えば $(x^{(0)}, y^{(0)}, z^{(0)}) := (0, 0, 0)$ ） $x^{(1)}, y^{(1)}, z^{(1)}$ を

とし, 以下同様に

で順次 $x^{(k)}, y^{(k)}, z^{(k)}$ を計算していけば解に近付く事がある. 実際, 今の場合を計算すれば

[ k] x y z
[ 0] 0.000 0.000 0.000
[ 1] 0.000 1.333 2.000
[ 2] -1.111 0.667 1.556
[ 3] -0.741 1.185 2.148
[ 4] -1.111 0.864 1.852
[ 5] -0.905 1.086 2.082
[ 6] -1.056 0.941 1.940
[ 7] -0.960 1.039 2.038
[ 8] -1.026 0.974 1.974
[ 9] -0.983 1.017 2.017
[10] -1.012 0.988 1.988
[11] -0.992 1.008 2.008
[12] -1.005 0.995 1.995
[13] -0.997 1.003 2.003
[14] -1.002 0.998 1.998
[15] -0.998 1.002 2.002

となり, 解 $(x, y, z) = (−1, 1, 2)$ に近付いている事が見える.

上記のように、繰り返せば繰り返すだけ解に近づいて行っているのが分かるかと思います。
これを用いて、本来は複雑な方程式を解いていくことになります。

ざーっと書いてきましたが、プログラムで扱うための前知識として各項について解説しました。

次回はこれを実際にプログラムに落とし込んで、今回実装した内容を解説しようと思います。

気づいた点や混乱した点のメモ

解説自体は以上なんですが、この実装をする前に色々と調べたものをだーっとメモしておこうと思います。（完全なる備忘録）
なのでここから先は完全に未来の自分宛てへのメモなので興味がある方だけ読んでください。

数式について調べていくうちに、いくつか気づいた点や理解する上で混乱した部分などをメモとして残しておきたいと思います。

移流項の内積は「発散ではない」

移流項は以下のように表されています。

$\nabla$ を内積のように作用させたものを「発散」と呼びますが、上記式の $\vec{u} \cdot \nabla$ は発散ではなく、単なる微分演算子との掛け算なので混同しないよう注意が必要です。

ちなみに「発散」は以下の式。

掛ける順番が違いますね。

こちらのPDFで言及されていて気づきました。

余談

後編の実装編を見てもらうと分かりますが、これは「速度分少しだけ移動したところの値を取ってくる」くらいの意味だと思います。（微分演算子ってことは「微小量」を表すので、「速度方向に少しだけ進んだ地点」を意味しているってことだと理解しています）

なお、こちらの「ナビエ・ストークス方程式を導出する」ではひとつずつ丁寧に導出してくれていて、その過程でどうしてこういう表記になったのかがイメージできました。

そこでの解説から式を引用させてもらうと以下のようになります。

なおここで、

であることに注意すると、

となります。この物理量fが速度uだったらどうなりますか？ Du/Dtは加速度ですよね。

そうすると(2-1)式はベクトルになって、それぞれの方向の式が出来上がります。

そして加速度ベクトルは

(2-2)式を一つの式にまとめようとするなら

となります。

ナビエ・ストークスの式に出てくる形ですね。

そしてこれはこうも考えることができます。
上記式は「ベクトルの勾配を取ったものとの発散を取る」ことになり、ランクは変わりません。（ランクについてはこちらの記事が分かりやすいです→ ベクトル解析の基本　発散　勾配　回転）

つまり、 $(u \cdot \nabla)u$ を計算してもベクトルの性質は残ったままになっている、というわけですね。
（ナブラ（ $\nabla$ ）についてはこの記事の後半に使い方などをまとめています）

ナビエ・ストークス方程式を、できるだけ平易に解説してくれている記事があるので紹介しておきます。

shimaphoto03.com

連続の式

上記解説で出てくる「連続の式」については以下の記事を参照。
要は、流体は連続しており、突然増えたり減ったりしないことを前提にしている、ということだと思います。

shimaphoto03.com

連続の式は流体力学における基本の式で「流体が突然発生したり、消滅したりしない」ということをコンセプトとしています。流体が発生したり、消滅したりしないのを示すには、流体を非常に非常に小さい要素に分割して、その要素内に出入りする流体の量に過不足がないという方程式を立てればよいのです。

全微分

全微分とは、ある関数の接線を1次関数で近似することを言います。
以下の記事に詳しく載っているので詳細はそちらをご覧ください。

mathwords.net

大事な点だけを引用させてもらうと以下のようになります。

接線の傾き（つまり、関数を１次関数で近似したときの傾き）が微分です。すなわち、 $f(x_0+h)=f(x_0)+ah+o(h)$ を満たす $a$ が $f(x) の x=x_0$ における微分係数です。ただし、 $o(h)$ は微小量 $（\lim_{h \to 0} \frac{o(h)}{h}=0$ を満たす関数）です。

さらに、

二変数関数の場合に確認してみます。全微分可能な場合、
$f(x_0 + h, y_0 + k) = f(x_0, y_0) + ah + bk + o(\sqrt{h^2 + k^2})$
という式が成立しますが、このとき $x$ についての偏微分は
$\lim_{h \to 0}\frac{f(x_0 + h, y_0) − f(x_0, y_0)}{h} = a$
となります（極限値が存在します）。同様に、 $y$ についての偏微分は $b$ となります。

つまり、全微分と偏微分の間には、
$a = \frac{\partial f}{\partial x}、b = \frac{\partial f}{\partial y}$
という関係式が成立します。言い換えると、全微分（一次近似式）に登場する一次の各係数は偏微分になります。よって、全微分可能な場合、
$df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y}dy$
などと書くことができます。