Unityの行列の扱いとベクトルのオーダー周りについてまとめておく

概要

自分で直に行列変換周りの処理を書くときに、掛ける順番やオーダー周りについていつも混乱するのでまとめておきます。

座標系の向き

これは、行列のオーダーには直接関係はありませんがよく混乱するので書いておきます。
Unityでは「左手系」の座標系を採用しています。

エディタ右上の軸情報を見ると、右が正、上が正、そして奥が正となる軸を取っていることが分かります。

f:id:edo_m18:20190103193700p:plain

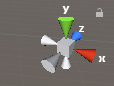
ちなみに左手系とは、左手の親指をX軸プラス、人差し指をY軸プラスにしたときに、それぞれの指に直行するように中指を曲げたときに指が向く方向がプラスとなる座標系です。

行列の配列要素の並び（メモリレイアウト）

さて、本題の行列に関して。
なぜ、列オーダー、行オーダーという名称があるのでしょうか。

その答えは行列の表現にあります。

数学的な「行列」はm x n行列となり、プログラムでは2次元配列として表すのが直感的です。
しかし3Dグラフィクスで扱う行列は通常、2次元配列ではなく1次元配列で表現されます。

そのため、行列の各要素をどういう順番で1次元配列として表現するか、が2通りあることが分かると思います。
つまり「列オーダー」と「行オーダー」です。

図にすると以下のような感じです。
行列の各要素が配列の添字としてはいくつなのか、を示しています。

f:id:edo_m18:20190103230507p:plain

実際に計算を行ってみると分かりますが、どちらの計算も必ず以下のように行列要素とベクトル要素が掛けられるようになっています。

// xだけ計算してみる
// 列オーダー版
x' = mat[0] * x + mat[4] * y + mat[8] * z + mat[12] * 1

// 行オーダー版
x' = x * mat[0] + y * mat[4] + z * mat[8] + 1 * mat[12]

基本的には「行列の計算」という数学上のルールに変化があるわけではないので、単純に配列のメモリレイアウトに依存して掛ける方向が変わる、ということですね。

列を主とするか、行を主とするかで添字が異なっているのが分かるかと思います。
これをしっかり把握しておかないと、行列の掛ける順番を間違えて想定していた結果にならない、ということが往々にしてあるわけです。

Unityでの掛ける順番は列オーダー

列オーダー、行オーダーを説明したところで、Unityではどういうふうに計算するのでしょうか。
まずはそれぞれのプラットフォーム（API）での規則を見てみます。

APIごとの規則

ちなみに既存のグラフィクスAPIの規則は以下となります。

API	座標系の向き	オーダー
OpenGL	右手系	列オーダー
DirectX	左手系	行オーダー
Unity	左手系	列オーダー

こうして並べてみると、Unityは「OpenGL」でさらに「左手系」の規則を採用、とどのAPIとも違う規則になっているのが分かりますね。

UnityのC#は「列オーダー」。でもシェーダは「行オーダー」

Unityのドキュメントを見てみると以下のように記載があります。

Matrices in unity are column major.

このことから、C#（CPU）の世界では「列オーダー」であることが分かります。

そして通常、行列はシェーダで利用するケースが多いでしょう。
マルチプラットフォームをサポートしているUnityのシェーダは「Cg」をベースとしたシェーダを記述するのが一般的です。
どうやらCgでは「行オーダー」であることが基本のようです。

そのためか、シェーダでは行優先としてメモリレイアウトがされるようです。
以下の記事で言及されていました。

tech.drecom.co.jp

Unityのシェーダーの世界は行優先であることが分かりました。

上記記事では、C#側で行と列それぞれに値を入れてシェーダ側でどう扱われるか、で判断したようです。

ただし、メモリレイアウトは切り替わっても転置されるわけではないのでご注意を。基本的に計算は列ベクトル前提で行います。

でも計算はC#、シェーダどちらも「列オーダー」

ということなので、基本的にはUnityで行列を扱っている以上は「列オーダー」で考えておいて大丈夫なようです。
実際、よく目にする頂点シェーダの記述も以下のようになっていて、列ベクトルを右側に置いて掛けているのが分かりますね。

// 列ベクトルなので「右側」にベクトルが置かれて計算されている
mul(UNITY_MATRIX_MVP, v.vertex);

行列の掛ける順番の意味

最後に、行列の掛ける順番について。
3Dグラフィクスでは行列が頻繁に使われ、特に、頂点シェーダからフラグメントシェーダに値を渡す際、一般的な合成行列を掛けて渡します。

具体的には以下の行列です。

モデル座標変換行列
ビュー座標変換行列
プロジェクション変換行列

そしてそれぞれの行列をひとつに「合算」させたものをシェーダに送り、それを各頂点に掛け算してフラグメントシェーダステージに渡す、というのが基本的な動作です。
そしてこれらの行列の頭文字を取ってM(odel) x V(iew) x P(rojection)でMVP行列、なんて呼ばれたりします。

しかしこれ、行オーダーで計算を行うAPI規則に基づくものです。（つまりDirectX）
Unityでは、上で示したように「列オーダー」となります。

そのため掛ける順番がMVPではなくPVMとなる点に注意が必要です。
コード例で示すと以下のようになります。

Matrix4x4 m = /* モデル座標変換行列生成 */;
Matrix4x4 v = anyCamera.worldToCameraMatrix;
Matrix4x4 p = GL.GetGPUProjectionMatrix(anyCamera.projectionMatrix);

// 掛ける順番が逆
Matrix4x4 mvp = p * v * m;

GL.GetGPUProjectionMatrixで変換を行う

少し余談となりますが、上記例にしれっと出てきたGL.GetGPUProjectionMatrix。
これは、プラットフォーム依存となる「正規化デバイス座標系」での、near / far表現を適切に変換するための処理をしてくれるヘルパー関数です。

こちらの処理については以下の記事がとても詳しく検証、解説してくれているのでそちらを参考にするのがいいでしょう。

【Unity】【数学】Unityでのビュー＆プロジェクション行列とプラットフォームの関係 – 株式会社ロジカルビート

また、数式を用いて解説を行ってくれているこちらの記事も参考に。

tech.drecom.co.jp

ざっくりとだけ解説しておくと、「正規化デバイス座標系」というのは、プロジェクション変換行列を適用し、均一な矩形領域（ビューボリューム）へと変換されたあとの座標系のことです。

そしてこの座標系の取るZの値が、APIによって異なります。
より具体的に言うと0～1となるのか、-1～1となるのか、という違いがあります。

これを適切に設定しないと、シェーダに値を送った際に意図した結果にならくなってしまいます。

なお、これを考慮した、自分で生成した行列をシェーダに送って、標準のMVP行列と同じような動作をさせるためには以下のように計算します。

// シーンビューでも適切に動くように`OnWillRenderObject`を利用して、Cameraの情報をそれぞれ取得
private void OnWillRenderObject()
{
    if (Camera.current == null)
    {
        return;
    }

    Camera cam = Camera.current;

    // スケールの行列
    Matrix4x4 sMat = Matrix4x4.Scale(_scale);
    // 平行移動行列
    Matrix4x4 tMat = Matrix4x4.Translate(_translate);
    // 上記2行列を「合成」し、さらにMVP行列になるように計算
    Matrix4x4 matrix = GL.GetGPUProjectionMatrix(cam.projectionMatrix, true) * cam.worldToCameraMatrix * tMat * sMat;

    // シェーダに送る
    _ren.material.SetMatrix("_Matrix", matrix);
}