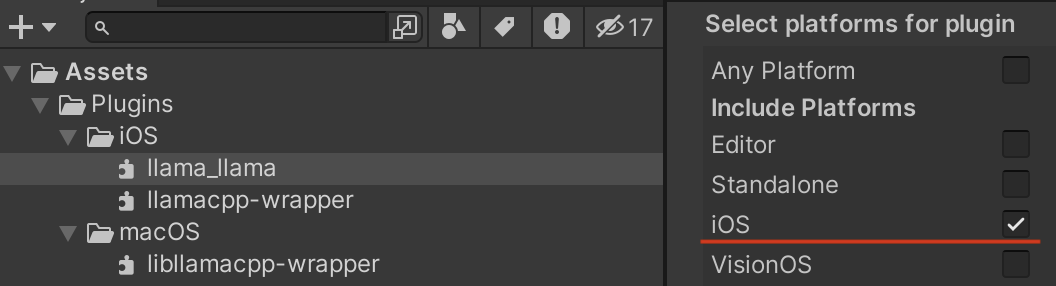
前回の記事では、ECS自体の使いどころやそもそもなぜ高速化するのかという点について書きました。
記事の中で紹介した動画はTextMesh Proの文字を利用して大量に文字を空間に表示するというものでした。
こんなやつ↓
文字を表示するMeshをQuadのものに統一してBatch Group化の効率を上げて描画してみたら、80,000文字でも余裕で60FPS以上出た。プロファイラ見ると250FPSくらいの速度出てる。#Unity #ECS pic.twitter.com/yNcbk69Ukd
— edom18@XR / MESON CTO (@edo_m18) 2024年4月7日
概要
今回はこのTextMesh Proの文字をECSで大量に描画する方法について書いていこうと思います。
今取り組んでいるプロジェクトで文字を大量に表示する必要があるため、ECSが利用できそうだったので実装してみました。
ちなみに先に注意点を書いておくと実はTextMesh Proそのものを描画しているわけではありません。実際にはQuadなMeshに対してTextMesh Proの文字のテクスチャアトラスを利用して描画しています。
具体的に言うと、TextMesh Proの持っているグリフというフォントに関する情報を利用してUVを算出して描画するということをしています。
なので今回はTextMesh Proの文字をどうやって表示したか、どう動かしているかについて書いていこうと思います。
今回の記事で解説している内容はGitHubにもアップしてあるので、実際に動作するものを見たい方はリポジトリをクローンして見てください。
TextMesh ProのテクスチャアトラスのUVを算出する
冒頭でも書いたように既存のTextMesh Proの文字をそのままECSで動かすことはできません。今回の実装はTextMesh Proの Glyph を用いてテクスチャアトラスのUV位置を算出し、それをECS上で描画できるようにしたものです。
そのためTextMesh Proの Glyph データからUVなどを算出する方法について解説します。
Glyphについて知る
TextMesh Proでは Glyph (グリフ)の情報を用いてテキストの描画を行っています。まずはこのグリフについて理解します。
グリフとは
モリサワのサイトから引用すると以下のように説明されています。
字体とほぼ同義語ですが、記述記号やスペースなども含めたものを指します。
慣用的にはデータとしての字体を指す場合に使われることもあります。これらの文字と記号類を集めたものがグリフセットと呼ばれるもので、これは文字セットや文字コレクションとほぼ同義と考えてよいでしょう。
つまり、文字をレンダリングする際に必要となるデータ、という感じですね。
TextMesh Proのグリフを使ったメッシュ作成のコード断片を見るとなんとなくイメージがわくと思います。
// TMP_Character型のデータからGlyphを取得する Glyph glyph = tmpCharacter.glyph; // 中略 float x0 = -glyphWidth * 0.5f; float x1 = glyphWidth * 0.5f; float y0 = -glyphHeight * 0.5f; float y1 = glyphHeight * 0.5f; Vector3[] vertices = new[] { new Vector3(x0, y0, 0), new Vector3(x0, y1, 0), new Vector3(x1, y1, 0), new Vector3(x1, y0, 0), };
こんな感じで Glyph 情報から文字の幅や高さ、またそれ以外でもカーニングや表示位置など様々な情報を得ることができます。つまり、文字を記述するための情報が得られる、というわけです。
※ 上記のコード例はUVではなく、文字のサイズなどに合わせたメッシュを生成するコードの一部です。今回の描画には直接的には関係ありません。
Glyphから情報を抜き出す
グリフ情報で様々な情報を得ることができることが分かりました。これらの情報を利用して、テクスチャアトラスのUV位置を算出します。
UVを算出する
さっそく、グリフ情報からUVの値を算出しましょう。
ただ、この算出に当たって注意点があります。通常、UVは各頂点ごとに設定されます。Quadのような形状であれば都合4つのUVの値が必要となります。しかし今回はメッシュを生成せず、デフォルトのQuadメッシュを利用するため頂点ごとにUVの値を設定することができません。そのため、少しだけ工夫が必要になります。
まず情報を整理すると、Quadのメッシュは左下が 0, 0、右上が 1, 1 となるUV値を持っています。図示すると以下のような値を持っています。
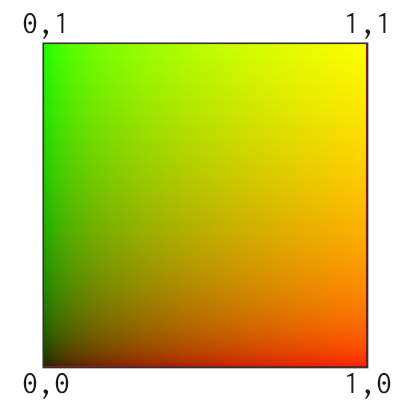
この値を加工してテクスチャアトラスのUVに合うようにできれば達成できそうです。
イメージとしては正方形を、望みの長方形に変形(縮小)した上で、テクスチャアトラスの該当位置まで移動させれば達成できそうですね。
次の画像がオフセットとスケールを調整するイメージです。ここでは「悟」という字に対して計算を行おうとしています。 ここでのゴールは、この「悟」という部分の赤い矩形の位置・サイズにぴったり重なるようにUVを加工することです。順に手順を見ていきましょう。

左下からX Offsetだけ右に移動し、Y Offsetだけ上に移動すると、「悟」の字の位置に原点( 0, 0 )が移動しますね。

文字サイズはそのままグリフ情報の幅と高さが使えます。そしてこれがそのままスケール値となります。
例えばスケールの値が横 0.05、縦 0.08 とした場合、Quadの4つのUVの値すべてに掛けて上げるとそれぞれ以下のようになります。(疑似コードで示します。左下から時計回りに値を設定していると仮定します)
float2 uv0 = new float2(0.0f * 0.05f, 0.0f * 0.08f); float2 uv1 = new float2(0.0f * 0.05f, 1.0f * 0.08f); float2 uv2 = new float2(1.0f * 0.05f, 1.0f * 0.08f); float2 uv3 = new float2(1.0f * 0.05f, 1.0f * 0.08f); // それぞれの値は以下になる。 // uv0 = ( 0.0, 0.0) // uv1 = ( 0.0, 0.08) // uv2 = (0.05, 0.0) // uv3 = (0.05, 0.08)
ちゃんと望みの値が得られていることが分かりますね。あとはこれに、前述のオフセットを足してやれば無事、テクスチャアトラスの文字をサンプリングするUVが得られる、というわけです。
この前提を元にUV値を算出している計算が以下です。
// グリフ情報を取得 Glyph glyph = tmpCharacter.glyph; // グリフのUVを計算 float rectWidth = glyph.glyphRect.width; float rectHeight = glyph.glyphRect.height; float atlasWidth = fontAsset.atlasWidth; float atlasHeight = fontAsset.atlasHeight; float rx = glyph.glyphRect.x; float ry = glyph.glyphRect.y; float offsetX = rx / atlasWidth; float offsetY = ry / atlasHeight; float uvScaleX = ((rx + rectWidth) / atlasWidth) - offsetX; float uvScaleY = ((ry + rectHeight) / atlasHeight) - offsetY; float4 uv = new float4(offsetX, offsetY, uvScaleX, uvScaleY);
ポイントはそれぞれの値の算出に、テクスチャアトラスのサイズを利用して正規化している点です。これによって適切にオフセットとスケールが求まります。
求めたこの値を使って、QuadのUVを加工することでテキストをECSでレンダリングすることができるようになります。
以下は、その計算を行っているShader Graphの様子です。

算出したUVのスケールの値を、Quadのスケールに乗算したあと、最後にオフセットを加算したものを最終のUVとしている様子です。
カスタムのUVをマテリアルに反映させる
UVの値を求め、それを利用するシェーダを準備することはできましたが、各文字のQuadごとに異なるUVを設定しなければなりません。通常の、MonoBehaviour なオブジェクトであれば個別にマテリアルに値を設定したり、あるいは MaterialPropertyBlock を使って設定することができます。しかし、ECSではそうした方法が使えません。
ではどうするのかというと、ECS側でオブジェクトごとに値を設定する方法が用意されているのでそれを利用します。
以下がそのドキュメントです。
シェーダ側の準備
ドキュメントに沿って方法を解説していきます。まずはシェーダ側の準備です。Shader Graphのプロパティの設定に Override Property Declaration という項目があります。これをまずオンにします。すると Shader Declaration という項目が設定できるようになるので、これを Hybrid Per Instance に変更します。
今回はカスタムのUVの値をオーバーライドしたいので CustomUv の設定でこれを行っています。これを設定しているのが以下の図です。
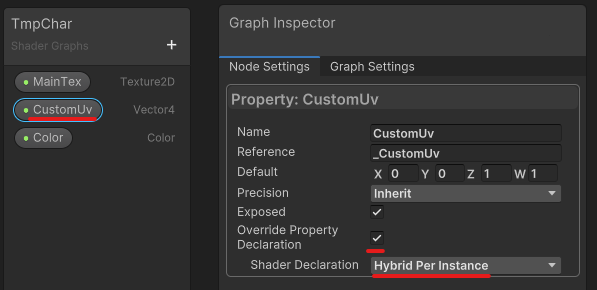
シェーダの設定は以上です。
カスタムUV用のコンポーネントを用意する
次に準備するのはコンポーネントです。ECSではコンポーネント、つまりデータが中心に存在するため、こうしたデータ周りはコンポーネントが担います。そしてECSでは、前述のマテリアルのオーバーライドを実現する方法を用意してくれているので、それに従ってコンポーネントを定義します。
大事な点は2点で、その他のコンポーネントと同様に IComponentData インターフェースを実装しつつ、さらに MaterialProperty 属性を付与する点です。属性の引数にはオーバーライドしたいプロパティ名を指定します。
具体的には以下のようになります。(抜粋ではなく、これはコード全文です)
using Unity.Entities; using Unity.Mathematics; using Unity.Rendering; [MaterialProperty("_CustomUv")] public struct CustomUvData : IComponentData { public float4 Value; }
値は、Shader Graphで定義したものと同じ型を指定します。(ここでは float4 )
そして MaterialProperty 属性の引数には _CustomUv を指定しています。あれ、 CustomUv じゃないの? と思われた方もいるかもしれませんが、設定の画像を見てもらうと Reference という項目の設定が _CustomUv になっているのが分かると思います。これは実際にシェーダで利用される変数名、ということなわけですね。なのでこれを指定します。
コンポーネントをEntityに追加する
最後に、定義したコンポーネントをEntityに登録します。登録はその他のコンポーネントとまったく同じです。
CustomUvData uvData = GetCustomUvData(index);
entityManager.AddComponentData(entity, uvData);
CustomUvData の生成処理は前述のUV算出のところで説明したものです。あとはそれをEntityManagerを通して登録してやればOKです。これをマテリアルに適用する処理はECS側のシステムが自動で行ってくれるため、特に開発者側でなにかをする必要はありません。
文字サイズを設定する
最後に計算するのは文字サイズを設定することです。今回利用しているのはデフォルトのQuadメッシュです。これは1m x 1mのサイズの面になるのでそのままだとかなり大きいポリゴンになってしまいます。
またそれ以外にも、本来は文字ごとにメッシュのサイズが異なります。例えば文字の A や x、! ではメッシュサイズが異なります。
ポリゴン形状を可視化するとこんな感じです。

この違いを各Quadに適用するのがここで解説する内容です。
グリフからメッシュのスケールを計算する
UVの計算で行ったのと似たようなことをします。UVの場合はテクスチャの位置とスケールを求めていました。今回はグリフからメッシュのサイズ、つまりQuadのスケールを計算します。
// フォントサイズ private float FontSizeToUnit => _fontSizeInCm * 0.01f; // ------------------- // グリフ情報を取得 Glyph glyph = tmpCharacter.glyph; // グリフの幅と高さを計算 float toUnit = FontSizeToUnit * (1f / fontAsset.faceInfo.pointSize); float glyphWidth = glyph.metrics.width * toUnit; float glyphHeight = glyph.metrics.height * toUnit; return new float3(glyphWidth, glyphHeight, 1f);
冒頭のフォントサイズは、デフォルトだと1m x 1mと巨大なので、それを補正( * 0.01f )しつつ、SerializeField で指定されたフォントサイズの大きさに調整するものです。例えばフォントサイズを 24 とした場合は実際には24cmの大きさになる、という具合です。
幅と高さの計算では、フォントサイズに対してフォントフェイスの持っているポイントサイズの逆数を掛けることで、続く幅などの値を正規化しています。( glyph.metrics.width などはフォントフェイスサイズになっているため)
そして最終的に幅と高さに対して前述の toUnit を掛けることで想定したサイズが求まります。
ここで求めた値はメッシュのサイズですが、適用するQuadは 1 x 1 のサイズなので、結果的にそのままこのサイズがスケールの値となるわけです。
以上で文字周りの生成、計算が終わりました。
次に、これらのメッシュを描画する手順について見ていきましょう。
Entityの描画はRenderMeshArrayを使う
まずはEntityを作成します。
World world = World.DefaultGameObjectInjectionWorld; EntityManager entityManager = world.EntityManager; Entity entity = entityManager.CreateEntity(); entityManager.SetName(entity, $"TextMeshEntity {index.ToString()}");
ECSのシステムそのものの解説はここでは割愛しますが、基本的な生成フローです。ECSのワールドからEntityManagerを取得し、それを利用してEntityを作成しています。
次に、生成したEntityに、描画するための設定を行っていきます。
※ そもそもECSは計算効率を最大化する目的なので必ずしもすべてのECSが描画されるとは限りません。そのため、描画したい場合は専用のコンポーネントなどを適切に設定する必要があるわけです。
RenderFilterSettings filterSettings = RenderFilterSettings.Default; filterSettings.ShadowCastingMode = ShadowCastingMode.Off; filterSettings.ReceiveShadows = false; RenderMeshDescription renderMeshDescription = new RenderMeshDescription { FilterSettings = filterSettings, LightProbeUsage = LightProbeUsage.Off, }; RenderMeshArray renderMeshArray = new RenderMeshArray(new[] { _material }, new[] { _mesh });
まずはコンポーネントの設定に必要なデータの定義から。
冒頭の RenderFilterSettings と RenderMeshDescription は描画に関する設定項目です。影を落とすか、Light Probeの影響は、などを設定しています。
その次にある RenderMeshArray がオブジェクト自体の設定になります。今回は Mesh も Material もひとつだけ設定していますが、配列で指定することで複数のメッシュとマテリアルをひとつにまとめて設定することができます。
最後は描画するEntityの設定において重要な RenderMeshUtility.AddComponents メソッドです。これは、描画に必要なコンポーネントを適切に設定してくれるヘルパーメソッドです。
RenderMeshUtility.AddComponents(
entity,
entityManager,
renderMeshDescription,
renderMeshArray,
MaterialMeshInfo.FromRenderMeshArrayIndices(0, 0));
RenderMeshUtility のクラスコメントを見ると以下のように書かれています。
/// Helper class that contains static methods for populating entities /// so that they are compatible with the Entities Graphics package. /// エンティティを実装するための静的メソッド含むヘルパークラス。 /// これによりEntities Graphicsパッケージに適合させることができる。
このユーティリティの AddComponents メソッドを通して描画に必要なコンポーネントが設定されます。適切にコンポーネントが設定されたEntityがある場合、ECSのシステム側で自動的に描画まで行ってくれます。これで文字が画面に表示されるようになりました。
RenderMesh と RenderMeshArray
ECSの描画について調べていく際、 RenderMesh を利用するということが書かれている記事もあり混乱しました。特に、見出しにある RenderMeshArray は配列を示唆することから、ひとつのEntityを描画するのに冗長なのでは、と思ってしまったのが混乱の元でした。
結論から言うと RenderMesh は現状ではどうやら非推奨となっており、 RenderMeshArray を利用するのが正規の方法のようです。なぜ配列を利用するのかは、そもそもECSを利用するモチベーションである「大量にオブジェクトを処理する」という観点から考えると自明です。
つまり、描画に関するコストを最小限にしたいという思想があり、そのためにメッシュを配列で持ち、それを切り替えることでGPUのステートの変更を最小限にする、ということを実現するためだと思われます。
ちなみに参考にした記事から引用させてもらうと以下のように書かれていました。
私が機能を見落とした可能性は否定できませんが、 以前まで使用されていたInstancing無しの描画クラスであるRenderMeshについて以下のような記述があり、サポートがされていないようでした。
// RenderMesh is no longer used at runtime, it is only used during conversion. // At runtime all entities use RenderMeshArray.そのため、オブジェクトがEntity化されると自動的にプログラム側はDOTS Instancingの適用条件を満たすということになります。 Shader側は別途条件を満たすために処理を追加する必要があります。
とのことなので、基本的に RenderMeshArray を使っておけば問題ないでしょう。
文字を動かすシステムを作成する
最後は文字を動かすシステムについて見ていきます。
システムの詳細についてはここでは割愛します。システムの実装方法やデータの取り回しについては前回の記事を参照してください。ここでは、今回作成したシステムそのものについてだけ解説します。
文字の動きを制御するジョブ
まず最初に見るのは、今回の文字を動かしている要でもあるジョブについてです。ECSでもC# Job Systemを使ってワーカースレッドで処理することができます。基本的に ISystem を実装したシステムであればジョブシステム化することも容易でしょう。
ECS用のジョブとして IJobEntity というインターフェースが用意されています。今回はこれを実装します。
今回の文字の動きを制御しているジョブの実装は以下のようになっています。
[BurstCompile] partial struct TmpUpdateJob : IJobEntity { public double Time; private void Execute([EntityIndexInQuery] int index, ref MeshInstanceData meshData, ref LocalToWorld localTransform) { double move = math.sin((Time * meshData.TimeSpeed + index) * math.PI) * meshData.MoveSpan; // index is just offset for the time. float3 position = meshData.Position + new float3(move); float angleSpeed = 0.005f; float angle = (float)math.sin(Time * meshData.TimeSpeed * angleSpeed * math.PI) * 360f; quaternion rotation = math.mul(meshData.Rotation, quaternion.RotateY(angle)); localTransform.Value = float4x4.TRS(position, rotation, meshData.Scale); } }
冒頭の [BurstCompile] 属性によってバーストコンパイラによるコンパイルを指示しています。バーストコンパイラでコンパイルすることができれば相当な高速化が見込めます。積極的に使っていきましょう。
実装自体は Execute メソッドを実装するだけです。しかし実は IJobEntity インターフェース自体はなにも宣言していない、ある意味マーカーのようなインターフェースとなっています。おそらくですが、ECSの大半がソースジェネレータによってコードが自動生成されるため、インターフェース周りも同じような制御になっているのでしょう。
そのため、 Execute メソッドの定義は必須となっていますが、引数に指定するものは柔軟に指定することができます。特に、そのジョブで利用するデータ型を指定することで、実行時に適切に対象データをシステムが提供してくれるようになります。
今回の例で言えば以下の部分ですね。
void Execute([EntityIndexInQuery] int index, ref MeshInstanceData meshData, ref LocalToWorld localTransform);
第一引数の [EntityIndexInQuery] 属性は、クエリの中でのEntityの位置を示しています。これを利用すると、コンピュートシェーダのスレッドIDのような使い方ができます。
そして続く第二、第三引数には実際に利用するコンポーネントの型を指定しています。今回はこのふたつだけのコンポーネントが必要でしたが、もしこれ以外にも必要な場合は引数として定義してやると、ECSのシステムが引数に対象コンポーネントを渡してくれるようになります。
値を更新するデータの場合は ref を、参照だけ(つまり読み取りだけ)する場合は in を指定します。あとはメソッドの実装部分で該当データを使って処理を行うだけです。今回は MeshInstanceData に初期値が入っているので、適当にSin関数などで回転や移動をしているだけです。
実際のプロジェクトではもっと意味のある処理をする必要がありますが、どうやって実装していくかがなんとなくイメージできるかと思います。
システムの全体を実装する
ジョブの実装が終わったので、あとはこのジョブを利用するシステムを実装します。今回のシステムではトランスフォーム、つまりメッシュの姿勢を制御する前に値を更新したいため、 [UpdateBefore()] 属性を指定して、トランスフォームの更新システムの前に処理されるように指示しています。
using Unity.Burst; using Unity.Entities; using Unity.Mathematics; using Unity.Transforms; [UpdateBefore(typeof(TransformSystemGroup))] public partial struct TmpSystem : ISystem { public void OnCreate(ref SystemState state) { state.RequireForUpdate<MeshInstanceData>(); state.RequireForUpdate<LocalToWorld>(); } [BurstCompile] public void OnUpdate(ref SystemState state) { var job = new TmpUpdateJob() { Time = SystemAPI.Time.ElapsedTime, }; job.ScheduleParallel(); } }
OnCreate メソッドでは、必要とするコンポーネントの種類を指定することができるため、今回は MeshInstanceData と LocalToWorld コンポーネントを持つEntityを対象とすることをシステムに伝えています。
そして OnUpdate で実際にジョブを生成し、スケジュールします。
システムの全体像は以上です。描画に関してはECSの RenderMeshSystem が自動で行ってくれるため、これ以上の実装は必要ありません。
まとめ
最終的に、テキストの色指定なども加えて以下のような見た目になりました。(iPhone 15 Proで動かしても60FPSを達成できています)
ECS使って160,000文字表示してみた。iPhone15Proでも余裕で60FPS出た。#Unity #ECS pic.twitter.com/aqGkaSNKNN
— edom18@XR / MESON CTO (@edo_m18) 2024年4月9日
ECSを利用すると、メモリアクセスの効率、ひいてはデータ転送の効率がいかに遅いかに気付かされます。処理負荷というとつい、計算のアルゴリズムや大量のオブジェクトの問題に目が行きがちですが、一番のボトルネックは「データ転送速度」というわけなのですね。
まったくの余談ですが、PolySpatialを用いたApple Vision Pro向けアプリ開発ではカスタムシェーダがほぼ使えず、Compute Shaderを用いたパーティクルなどの描画が行えません。現状ではECSもレンダリングできないのですが、シェーダのカスタムよりは実現可能性が高いのかな、と思っているので密かにECSに期待しています。
ぜひみなさんもECSで大量のオブジェクトをコントロールする楽しさに触れてみてください。