概要
今回はOBB(Oriented Bounding Box)についてのまとめです。
今実装している中でボリュームのサイズをある程度正確に量りたいと思ったのが理由です。
今回の実装はこちらの記事を参考に、いくつかの記事を参照して行いました。
こちらの記事に書かれている手順を引用させていただくと以下のようになります。
- 頂点座標で行列を作る(xyz座標3データ×5000個のデータで3×5000の行列)
- xyz各行の平均を計算して引く
- 引いた行列の転置行列を作る(5000×3の行列)
- 掛けてNで割って共分散行列ができる((3×5000)×(5000×3)→3×3の行列)
- ヤコビ法などを用いて共分散行列の固有値・固有ベクトルを計算する
- 固有値と固有ベクトルが求まれば、固有値の大きい順に固有ベクトルを並べ替えます。
- 固有ベクトルを並べて3×3の行列を作っておきます。
- 固有ベクトルの行列と頂点の内積を計算し、各固有ベクトル毎に最大と最小の内積値を計算します。
- そのデータを使えば重心、OBBの座標が計算できます。(参考サイト参照)
ひとつひとつ見ていきましょう。
OBBとは
OBBとはOrientedと名前がついている通り、オブジェクトに対してできるだけ余白が出ないようにそれをすっぽりと覆うBoxを定義します。
それとは別にAABB(Axis Aligned Bounding Box)があります。Axis Alignedの名前の通り、座標空間のXYZ軸(Axis)に平行(Aligned)なBoxです。
つまり、オブジェクトが回転すると場合によっては無駄な余白ができてしまいます。
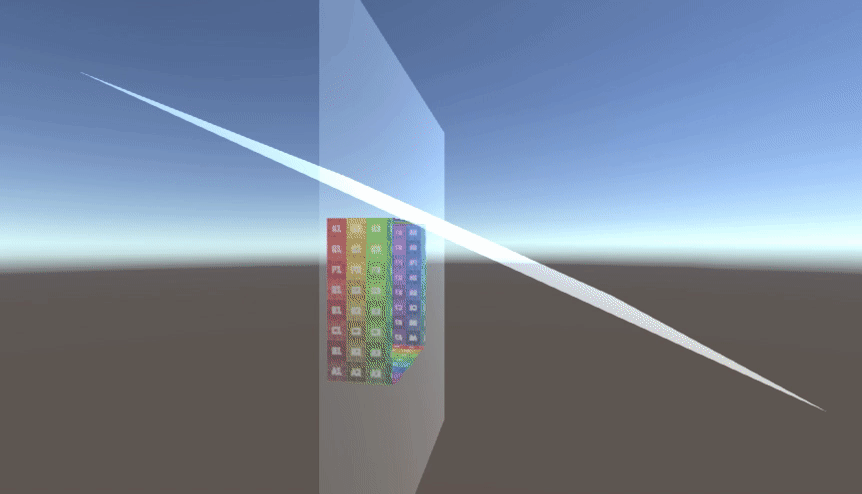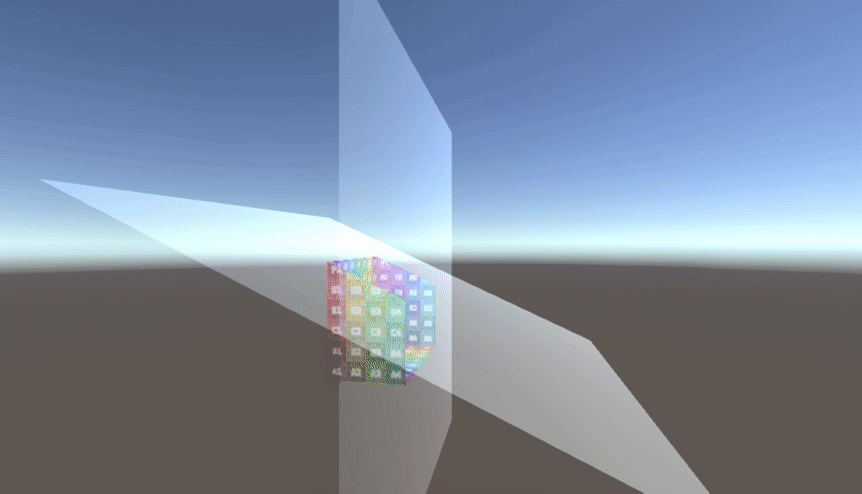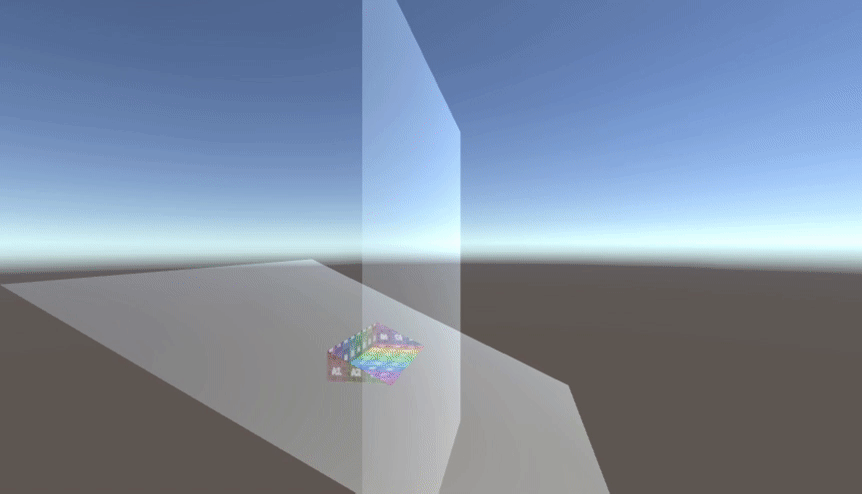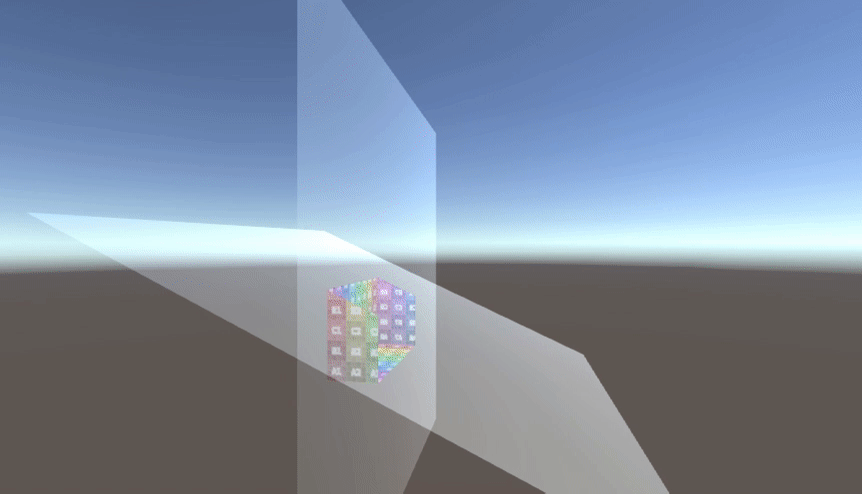
それぞれ図にすると以下のような感じの違いになります。

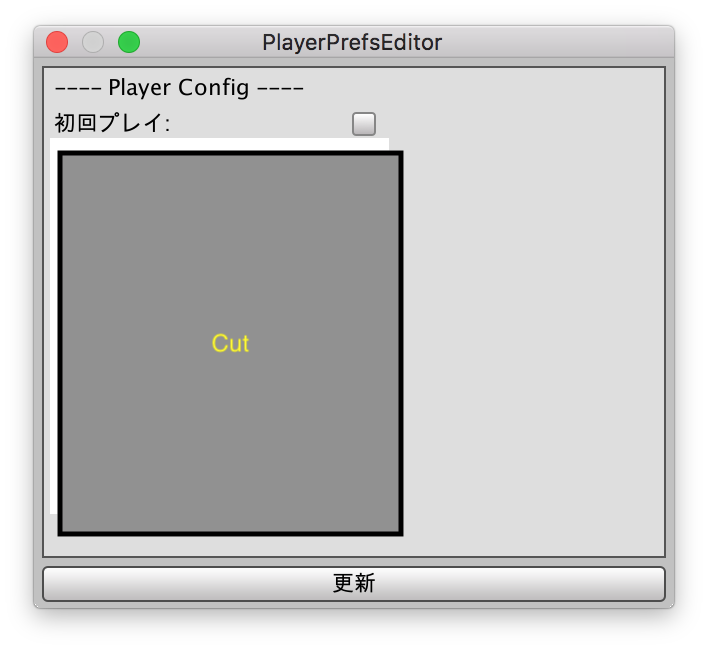
▲球体を半分にカットしてAABBを表示した状態

▲上記をOBBで表示した状態
いかがですか。オブジェクトの形状や回転状態によってだいぶ違いが出るのが分かるかと思います。
OBBの実装の概要についてはこちらの記事が参考になります。
記事から引用させていただくと、
簡単に言うと、あるポリゴン群に対してどんな方向を向いていてもかまわないので、それをすっぽりと囲む、できる限り小さな直方体を作りましょうというのがOBBの手法です。
この直方体をいかにして作るのかという所が腕の見せ所になります。
とりあえずここでは、上記論文で紹介されている主成分分析を使うことにしましょう。
と書かれています。
主成分分析とは
記事で書かれている主成分分析とはなんでしょうか。
Wikipediaによるとこう書かれています。
主成分分析(しゅせいぶんぶんせき、英: principal component analysis; PCA)とは、相関のある多数の変数から相関のない少数で全体のばらつきを最もよく表す主成分と呼ばれる変数を合成する多変量解析の一手法[1]。データの次元を削減するために用いられる。
主成分を与える変換は、第一主成分の分散を最大化し、続く主成分はそれまでに決定した主成分と直交するという拘束条件の下で分散を最大化するようにして選ばれる。主成分の分散を最大化することは、観測値の変化に対する説明能力を可能な限り主成分に持たせる目的で行われる。選ばれた主成分は互いに直交し、与えられた観測値のセットを線型結合として表すことができる。言い換えると、主成分は観測値のセットの直交基底となっている。主成分ベクトルの直交性は、主成分ベクトルが共分散行列(あるいは相関行列)の固有ベクトルになっており、共分散行列が実対称行列であることから導かれる。
なんだか分かったような分からないようなw
自分の理解としては、多数ある点群に対して方向性を見出し、それを計算によって求めた値を掛けることで分析しやすい形にする、といった感じでしょうか。
固有値・固有ベクトルとは
主成分分析には「固有値・固有ベクトル」を使って変換が行われるようです。
固有値、固有ベクトルについては以下の記事がとても分かりやすかったです。
なんだかどんどん主題と離れていっている気がしなくもないですが、まぁせっかくなのでまとめておきましょうw
上で紹介した記事を見てもらうとアニメーションで示してくれているのでとても分かりやすいですが、自分の理解として言葉で説明しておくと。
とあるベクトルに対して、とある行列を掛けたとき、そのベクトルが回転せず定数倍になるベクトルのことを「固有ベクトル」、そしてその定数倍の定数が「固有値」、ということのようです。
数式で表すと以下になります。
※ ただし
が行列で
が定数(スカラー)です。
行列での演算が定数(スカラー)の演算で表せる、というのが上記式の意味です。
(推測ですが)統計学や主成分分析に使える理由としては、傾向がある=回転しないベクトル(方向)、みたいなことから来ているんでしょうか。
ちょっと数学に疎いのでそのあたりの深い話は分かりません・・・。
閑話休題。
さて、最初に紹介した記事を読み進めると以下のように続いています。
OBBではデータとはポリゴンの頂点群なので、x,y,zの3次元のデータが頂点の個数分存在します。 それを使って分散共分散行列を作って、その行列の固有ベクトルを計算すると、 OBBを表す3つの軸が得られます。
さぁ、また新しい単語が出てきましたw
分散共分散行列とは
ここでもWikipediaから引用させてもらうと、
統計学と確率論において分散共分散行列(ぶんさんきょうぶんさんぎょうれつ、英: variance-covariance matrix)や共分散行列(きょうぶんさんぎょうれつ、英: covariance matrix)とは、ベクトルの要素間の共分散の行列である。これは、スカラー値をとる確率変数における分散の概念を、多次元に自然に拡張したものである。
と書かれています。
「分散」と「共分散」があり、それを合成した行列のためこう呼ばれるようです。
ちなみに、「分散共分散行列」については以下の記事がとても分かりやすかったです。
分散
まずは分散について。
これまたWikipedia)から引用すると、
確率論および統計学において、分散(ぶんさん、英: variance)は、確率変数の2次の中心化モーメントのこと。これは確率変数の分布が期待値からどれだけ散らばっているかを示す非負の値である[1]。
つまり、確率変数がどれだけ「分散」しているか、ということかな。
また、上で紹介した記事を見てみると、以下のように説明されています。
具体的には、分散は「(各データの平均値からの距離)の2乗の平均」。
分散は2乗であることに注意。単位をそろえるために、分散の平方根を取ったものが標準偏差。
標準偏差をσで表すと、分散はσ2で表される。
とのこと。なるほど。
ちなみに「標準偏差」については以下の記事が分かりやすかったです。
いわゆる「偏差値」とか、その類の話ですね。
二乗する辺りが「なるほど」と思わされます。
つまり、平均値からの距離を二乗することにより、大きく散らばっている(大きく分散している)場合ほど偏差が大きくなる、というわけです。(大きな値の二乗はより大きな数値になる)
そして完全に余談ですが、以前、「[数学] 最小二乗平面をプログラムで求める」という記事を書いていてそこでも似た話が出てくるので興味がある方は読んでみてください。
共分散
こちらもWikipediaから引用すると、
共分散(きょうぶんさん、covariance)は、2 組の対応するデータ間での、平均からの偏差の積の平均値である[1]。2 組の確率変数 X, Y の共分散 Cov(X, Y) は、E で期待値を表すことにして、 Cov(X, Y) = E[(X - E[X])(Y - E[Y])] で定義する。
上で、分かりやすいと紹介した記事を読んでの自分の理解を書くと、異なるデータに対して分散を計算し、どれくらい相関があるか、を計算したものが共分散かな、と思っています。
ちなみにその記事では以下のように例えています。非常に分かりやすい。
例えば、生徒の「数学の点数」と「英語の点数」がどのような関係にあるか知りたい。数学ができる生徒はやはり英語ができるのか?(正の相関)、それとも数学ができる生徒は英語が苦手なのか(負の相関)。
そこで、数学の点数(xの値)と英語の点数(yの値)という、2つのデータ群を考慮した分散を「共分散」と呼び、この共分散Sxyは次の式で表される。
※ は転置
つまり、XとYというふたつのデータがあった場合、上記式で求まるXとYの相関を見るのがXYの共分散となります。
さらにXとXの共分散が分散、ということのようです。
式にすると以下。
分散と共分散が分かりました。あとはこれを行列の形に合成すると「分散共分散行列」となります。
行列の形は以下のようになるようです。
OBBの話に戻すと、「頂点郡」というバラけたデータから、XYZという3要素がどれくらい相関しているか、を主成分分析によって求める、みたいなことなのかなーと想像しています。(あくまで想像)
さて、では実際にどうこの分散共分散行列を求めるかと言うと、冒頭の記事の引用を再掲すると以下のように書かれています。
- 頂点座標で行列を作る(xyz座標3データ×5000個のデータで3×5000の行列)
- xyz各行の平均を計算して引く
- 引いた行列の転置行列を作る(5000×3の行列)
- 掛けてNで割って共分散行列ができる((3×5000)×(5000×3)→3×3の行列)
分散共分散行列の意味の解説を元に見てみるとやっていることはまさに同じことですね。
そして冒頭の記事が参考にしている記事には以下のようなコードが示されています。
Vertex配列に頂点データが入っていて、配列の長さがSizeになります。
mは全頂点の平均値です。
float C11 = 0, C22 = 0, C33 = 0, C12 = 0, C13 = 0, C23 = 0;
for( int i = 0; i < Size; ++i ) {
C11 += ( Vertex[i].x - m.x ) * ( Vertex[i].x - m.x );
C22 += ( Vertex[i].y - m.y ) * ( Vertex[i].y - m.y );
C33 += ( Vertex[i].z - m.z ) * ( Vertex[i].z - m.z );
C12 += ( Vertex[i].x - m.x ) * ( Vertex[i].y - m.y );
C13 += ( Vertex[i].x - m.x ) * ( Vertex[i].z - m.z );
C23 += ( Vertex[i].y - m.y ) * ( Vertex[i].z - m.z );
}
C11 /= Size;
C22 /= Size;
C33 /= Size;
C12 /= Size;
C13 /= Size;
C23 /= Size;
float Matrix[3][3] = {
{ C11, C12, C13 },
{ C12, C22, C23 },
{ C13, C23, C33 },
};
平均からの距離を求めて、それを行列にしている部分ですね。
ただ、いくつかの行列要素は同じ計算結果になるため必要な部分だけを計算して行列にしているのが分かります。
これで「分散共分散行列」を求めることができます。
次にここから「固有ベクトル」を求め、OBBの軸を求めます。
なお、コードを紹介してくれた記事では以下のように続いています。
こうして得られる分散共分散行列ことMatrix[3][3]は、
実対称行列なのでjacobi法で固有ベクトルを求めることができます。
固有ベクトルを求める
さて、だいぶ遠回りしてしまいましたが、ふんわりと、どういう処理を用いてOBBを計算するのかを見てきました。
最後に、求めたいのはOBBの軸と長さです。
3軸の向きと長さが分かればそこからOBBを求めることができますね。
ということで固有ベクトルを求める計算です。
jacobi法(ヤコビ法)で固有ベクトルを求める
前述の通り、分散共分散行列を求め、そこからjacobi法(ヤコビ法)という手法を用いて固有ベクトルを求めます。
jacobi法についてはこちらの記事(Jacobi法 - [物理のかぎしっぽ])を参考にさせていただきました。
該当記事の冒頭の解説を引用させてもらうと、
Jacobi法(ヤコビ法)を用いて行列の固有値と固有ベクトルを求めてみたいと思います. Jacobi法では対称行列しか扱えないという制約があるものの,アルゴリズム自体も簡単な上に,解が必ず実数になる事もあり,大変シンプルです.
とあります。
そして分散共分散行列は対称行列のためこの方法が使える、というわけのようです。
さて、実際の求め方ですが、引用させていただくと、
となるとき,行列Aと行列Bの固有値は一致します.また,行列Aが対称行列である場合,直交行列Pを用いて
と,対角化することができ,行列Λの対角成分は行列Λの固有値となります.ここで直交行列Pの列ベクトルとそれに対応する行列Λの列の対角成分は固有値と固有ベクトルの関係となります.このことから行列Aの固有値と固有ベクトルを求めるには,行列Aを対角化する直交行列Pを求めれば良いことになります.
Jacobi法ではこの直交行列Pを反復作業で求めています.つまり,行列Aの非対角成分の1つをゼロにする直交行列を用い,
とする事を繰り返します.[tex: P^{-1}n … P^{-1}4 P^{-1}3 P^{-1}2 P^{-1}_1 AP_1 P_2 P_3 P_4 … P_n = \Lambda]
これを繰り返し全ての非対角成分をゼロにし,対角化をするのがJacobi法です.また,
この部分が行列Aを対角化する直交行列であり,列ベクトルは固有ベクトルとなります.
上記の説明の中で出てくる式や単語を整理しておきます。
「直交行列」ですが、意味は逆行列と転置行列が等しくなる正方行列のことです。以下を満たす行列ですね。
また「対角化」を調べてみると以下の記事が分かりやすいです。
記事から説明を引用すると、
与えられた正方行列 A に対して,正則行列 P をうまく取ってきて
を対角行列にする操作を対角化と言う。
ヤコビ法で語られていた以下の式が出てきました。
ここで「正則行列Pをうまく取ってきて」とあります。
つまりこの「うまく取ってくる」というのがヤコビ法、ということになりますね。
さて実際のヤコビ法の計算方法ですが、詳細は紹介した記事を読んでみてください。
プログラムでの計算方法も掲載されています。
今回はそのプログラムコードを参考にさせていただき、Unity上で使えるようにC#で書き直しました。
C#コード
最後に、実際に書いたコードを掲載しておきます。よかったら参考にしてみてください。
以下のコードを貼り付けて実行すると、下図のようにOBBが表示されます。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class OBBTest : MonoBehaviour
{
private float _max = 0.0001f;
private Vector3[] _edges = new Vector3[0];
private Vector3 _origin;
private void OnDrawGizmos()
{
if (_edges.Length == 0)
{
return;
}
Gizmos.color = Color.yellow;
Gizmos.DrawWireSphere(_origin, 0.01f);
Gizmos.color = Color.blue;
Vector3 from, to;
Vector3 ftr = _origin + (_edges[0] * 0.5f) + (_edges[1] * 0.5f) + (_edges[2] * 0.5f);
Vector3 fbr = ftr - _edges[2];
Vector3 ftl = ftr - _edges[0];
Vector3 fbl = ftl - _edges[2];
Vector3 btr = ftr - _edges[1];
Vector3 bbr = btr - _edges[2];
Vector3 btl = btr - _edges[0];
Vector3 bbl = btl - _edges[2];
Gizmos.DrawLine(ftr, fbr);
Gizmos.DrawLine(ftr, ftl);
Gizmos.DrawLine(ftl, fbl);
Gizmos.DrawLine(fbl, fbr);
Gizmos.DrawLine(btr, bbr);
Gizmos.DrawLine(btr, btl);
Gizmos.DrawLine(btl, bbl);
Gizmos.DrawLine(bbl, bbr);
Gizmos.DrawLine(ftr, btr);
Gizmos.DrawLine(ftl, btl);
Gizmos.DrawLine(fbr, bbr);
Gizmos.DrawLine(fbl, bbl);
}
private void Awake()
{
CalcEdges();
}
private void Update()
{
if (Input.GetKeyDown(KeyCode.U))
{
CalcEdges();
}
}
private void CalcEdges()
{
MeshFilter filter = GetComponent();
Vector3[] vertices = filter.mesh.vertices;
float[,] eigenVectors = GetEigenVectors(CollectMatrix(vertices));
int rank = eigenVectors.Rank;
Vector3 vec1, vec2, vec3;
{
float x = eigenVectors[0, 0];
float y = eigenVectors[1, 0];
float z = eigenVectors[2, 0];
vec1 = new Vector3(x, y, z);
}
{
float x = eigenVectors[0, 1];
float y = eigenVectors[1, 1];
float z = eigenVectors[2, 1];
vec2 = new Vector3(x, y, z);
}
{
float x = eigenVectors[0, 2];
float y = eigenVectors[1, 2];
float z = eigenVectors[2, 2];
vec3 = new Vector3(x, y, z);
}
// 全頂点に対して内積を取り、最小値・最大値を計算する
float min1 = float.MaxValue;
float min2 = float.MaxValue;
float min3 = float.MaxValue;
float max1 = float.MinValue;
float max2 = float.MinValue;
float max3 = float.MinValue;
for (int i = 0; i < vertices.Length; i++)
{
Vector3 pos = vertices[i];
float dot1 = Vector3.Dot(vec1, pos);
if (dot1 > max1)
{
max1 = dot1;
}
if (dot1 < min1)
{
min1 = dot1;
}
float dot2 = Vector3.Dot(vec2, pos);
if (dot2 > max2)
{
max2 = dot2;
}
if (dot2 < min2)
{
min2 = dot2;
}
float dot3 = Vector3.Dot(vec3, pos);
if (dot3 > max3)
{
max3 = dot3;
}
if (dot3 < min3)
{
min3 = dot3;
}
}
float len1 = max1 - min1;
float len2 = max2 - min2;
float len3 = max3 - min3;
Vector3 edge1 = transform.localToWorldMatrix.MultiplyVector(vec1 * len1);
Vector3 edge2 = transform.localToWorldMatrix.MultiplyVector(vec2 * len2);
Vector3 edge3 = transform.localToWorldMatrix.MultiplyVector(vec3 * len3);
_edges = new[]
{
edge1, edge2, edge3,
};
Vector3 center1 = (vec1 * (max1 + min1)) * 0.5f;
Vector3 center2 = (vec2 * (max2 + min2)) * 0.5f;
Vector3 center3 = (vec3 * (max3 + min3)) * 0.5f;
_origin = transform.localToWorldMatrix.MultiplyPoint(center1 + center2 + center3);
}
private float[,] CollectMatrix(Vector3[] vertices)
{
// 各成分の平均を計算
Vector3 m = Vector3.zero;
for (int i = 0; i < vertices.Length; i++)
{
m += vertices[i];
}
m /= vertices.Length;
float c11 = 0; float c22 = 0; float c33 = 0;
float c12 = 0; float c13 = 0; float c23 = 0;
for (int i = 0; i < vertices.Length; i++)
{
c11 += (vertices[i].x - m.x) * (vertices[i].x - m.x);
c22 += (vertices[i].y - m.y) * (vertices[i].y - m.y);
c33 += (vertices[i].z - m.z) * (vertices[i].z - m.z);
c12 += (vertices[i].x - m.x) * (vertices[i].y - m.y);
c13 += (vertices[i].x - m.x) * (vertices[i].z - m.z);
c23 += (vertices[i].y - m.y) * (vertices[i].z - m.z);
}
c11 /= vertices.Length;
c22 /= vertices.Length;
c33 /= vertices.Length;
c12 /= vertices.Length;
c13 /= vertices.Length;
c23 /= vertices.Length;
float[,] matrix = new float[,]
{
{ c11, c12, c13 },
{ c12, c22, c23 },
{ c13, c23, c33 },
};
return matrix;
}
///
/// 行列の中の絶対値の最大値とその位置を返す
///
/// 評価する行列
/// 最大値の行位置
/// 最大値の列位置
/// 最大値
private float GetMaxValue(float[,] matrix, out int p, out int q)
{
p = 0;
q = 0;
int rank = matrix.Rank;
float max = float.MinValue;
for (int i = 0; i < rank; i++)
{
int len = matrix.GetLength(i);
for (int j = 0; j < len; j++)
{
// 対角成分は評価しない
if (i == j)
{
continue;
}
float absmax = Mathf.Abs(matrix[i, j]);
if (max <= absmax)
{
max = absmax;
p = i;
q = j;
}
}
}
if (p > q)
{
int temp = p;
p = q;
q = temp;
}
return max;
}
///
/// 固有ベクトルを得る
///
/// 評価する行列
private float[,] GetEigenVectors(float[,] matrix)
{
// 固有ベクトルのための行列を正規化
float[,] eigenVectors = new float[3,3];
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
if (i == j)
{
eigenVectors[i,j] = 1f;
}
else
{
eigenVectors[i,j] = 0;
}
}
}
int limit = 100;
int count = 0;
int p, q;
while (true)
{
count++;
if (count >= limit)
{
Debug.Log("somothing was wrong.");
break;
}
float max = GetMaxValue(matrix, out p, out q);
if (max <= _max)
{
break;
}
float app = matrix[p, p];
float apq = matrix[p, q];
float aqq = matrix[q, q];
float alpha = (app - aqq) / 2f;
float beta = -apq;
float gamma = Mathf.Abs(alpha) / Mathf.Sqrt(alpha * alpha + beta * beta);
float sin = Mathf.Sqrt((1f - gamma) / 2f);
float cos = Mathf.Sqrt((1f + gamma) / 2f);
if (alpha * beta < 0)
{
sin = -sin;
}
for (int i = 0; i < 3; i++)
{
float temp = cos * matrix[p, i] - sin * matrix[q, i];
matrix[q, i] = sin * matrix[p, i] + cos * matrix[q, i];
matrix[p, i] = temp;
}
for (int i = 0; i < 3; i++)
{
matrix[i, p] = matrix[p, i];
matrix[i, q] = matrix[q, i];
}
matrix[p, p] = cos * cos * app + sin * sin * aqq - 2 * sin * cos * apq;
matrix[p, q] = sin * cos * (app - aqq) + (cos * cos - sin * sin) * apq;
matrix[q, p] = sin * cos * (app - aqq) + (cos * cos - sin * sin) * apq;
matrix[q, q] = sin * sin * app + cos * cos * aqq + 2 * sin * cos * apq;
for (int i = 0; i < 3; i++)
{
float temp = cos * eigenVectors[i, p] - sin * eigenVectors[i, q];
eigenVectors[i, + q] = sin * eigenVectors[i, p] + cos * eigenVectors[i, q];
eigenVectors[i, + p] = temp;
}
}
return eigenVectors;
}
}