CustomRenderTextureを使って波紋エフェクトを作る
概要
何番煎じか分かりませんが、CustomRenderTextureを使ってシェーダでお絵かきができると色々表現の幅が増えるので、それの練習のために表題のサンプルを作ってみました。
↓実際に動かしたの動画
CustomRenderTextureでシミュレーションした波形でバンプマップしてみた。 pic.twitter.com/OXhkAitOiD
— edom18@XR / MESON CTO (@edo_m18) 2018年8月22日
サンプルはCustomRenderTextureを使って波動方程式を解き波形を描画、さらにそれをレンダリング用シェーダの法線マップとして入力し、歪みとライティング(ランバート反射とフォン反射)を適用してみたものです。
ダウンロード
今回のサンプルもGithubにアップしてあります。
CustomRenderTextureとは
ドキュメントは以下です。
https://docs.unity3d.com/ja/current/Manual/CustomRenderTextures.htmldocs.unity3d.com
ドキュメントから引用させてもらうと、
カスタムレンダーテクスチャはレンダーテクスチャの拡張機能で、これを使うと簡単にシェーダー付きのテクスチャを作成できます。これは、コースティクス、雨の効果に使われるリップルシミュレーション、壁面へぶちまけられた液体など、あらゆる種類の複雑なシミュレーションを実装するのに便利です。また、カスタムレンダーテクスチャはスクリプトやシェーダーのフレームワークを提供し、部分的更新、または、マルチパスの更新、更新頻度の変更などのさらに複雑な設定をサポートします。
つまり、波形などの複雑なシミュレーションを必要とする演算をシェーダベースで行い、それをテクスチャとして利用できるようにしてくれる機能です。
この機能の面白いところは、updateや初期化などはある程度テクスチャ側の設定項目でまかなえるので、シェーダだけでも完結できる点にあります。
つまりC#スクリプトはいらないということです。
もちろん、細やかな制御をするためにスクリプトから制御することも可能です。
今回の波紋シミュレーションではスクリプトによる更新はしていません。
そしてそれを法線マップとして利用することで冒頭の動画のようなエフェクトを生成しています。
CustomRenderTexture用のcgincがある
さて、では実際に実装を行っていきます。
CustomRenderTextureは前述の通り、シェーダ(マテリアル)を設定するだけでその結果をRenderTextureに保持してくれる便利なものです。
そのため、RenderTextureに保存したい絵を描くためのシェーダを書く必要があります。
(ちなみに、CustomRenderTextureが登場する前は、C#も動員して自分で保存などの処理を書く必要がありました)
まずはCustomRenderTexture向けのシェーダで利用するものを紹介します。
// 専用のcgincファイル
#include "UnityCustomRenderTexture.cginc"
// 専用の定義済みvertexシェーダ関数
#pragma vertex CustomRenderTextureVertexShader
// 専用の構造体
struct v2f_customrendertexture { ... }
// テクスチャサイズを取得
float width = _CustomRenderTextureWidth;
float height = _CustomRenderTextureHeight;
// UV座標を取得
float2 uv = i.globalTexcoord;
// CustomRenderTextureからテクセルをフェッチ
float3 c = tex2D(_SelfTexture2D, uv);
Unityでシェーダを書いたことがある人であればどう使うのかイメージ付くかと思います。 CustomRenderTexture向けにシェーダを書く場合、上記のようにいくつか専用のものが定義されているのでそれを利用します。
これらを使ってCurstomRenderTextureにお絵かきするシェーダを書いていきます。
CustomRenderTexture用シェーダを書く
では実際のシェーダを書いていきます。
波動方程式を解く
CustomRenderTextureで利用するシェーダが分かったところで、実用的な使い方として波動方程式を解いた波形を描いてみたいと思います。
ちなみに、以前自分もQiitaの記事で波動方程式について書いているので、よかったらそちらも参考にしてみてください。(実装はWebGLですが)
上の記事は以下の動画を元に実装したものになります。
波動方程式について、高校数学でも分かるような感じで丁寧に説明してくれていてとても分かりやすいのでオススメです。
なお今回の実装はこちらの凹みさんの記事を参考にさせていただきました。
波動方程式を解くシェーダ(for CustomRenderTexture)
下記シェーダは上記の凹みさんの記事で書かれているものを利用させていただきました。
それを少し整形し、自分がコメントを追記したものです。
Shader "Hidden/WaveShader"
{
Properties
{
_S2("PhaseVelocity^2", Range(0.0, 0.5)) = 0.2
_Atten("Attenuation", Range(0.0, 1.0)) = 0.999
_DeltaUV("Delta UV", Float) = 3
}
SubShader
{
Cull Off
ZWrite Off
ZTest Always
Pass
{
CGPROGRAM
#pragma vertex CustomRenderTextureVertexShader
#pragma fragment frag
#include "UnityCustomRenderTexture.cginc"
half _S2;
half _Atten;
float _DeltaUV;
sampler2D _MainTex;
float4 frag(v2f_customrendertexture i) : SV_Target
{
float2 uv = i.globalTexcoord;
// 1pxあたりの単位を計算する
float du = 1.0 / _CustomRenderTextureWidth;
float dv = 1.0 / _CustomRenderTextureHeight;
float3 duv = float3(du, dv, 0) * _DeltaUV;
// 現在の位置のテクセルをフェッチ
float2 c = tex2D(_SelfTexture2D, uv);
// ラプラシアンフィルタをかける
// |0 1 0|
// |1 -4 1|
// |0 1 0|
float k = (2.0 * c.r) - c.g;
float p = (k + _S2 * (
tex2D(_SelfTexture2D, uv - duv.zy).r +
tex2D(_SelfTexture2D, uv + duv.zy).r +
tex2D(_SelfTexture2D, uv - duv.xz).r +
tex2D(_SelfTexture2D, uv + duv.xz).r - 4.0 * c.r
)) * _Atten;
// 現在の状態をテクスチャのR成分に、ひとつ前の(過去の)状態をG成分に書き込む。
return float4(p, c.r, 0, 0);
}
ENDCG
}
}
}
これを適切にCustomRenderTextureにセットすると以下のようにシミュレーションが進んでいきます。

CustomRenderTextureのセットアップ
シェーダが書けたところで、実際に使用するためにセットアップを行っていきます。
CustomRenderTextureの生成
まずはCustomRenderTextureを生成します。
生成には以下のようにメニューから生成することができます。
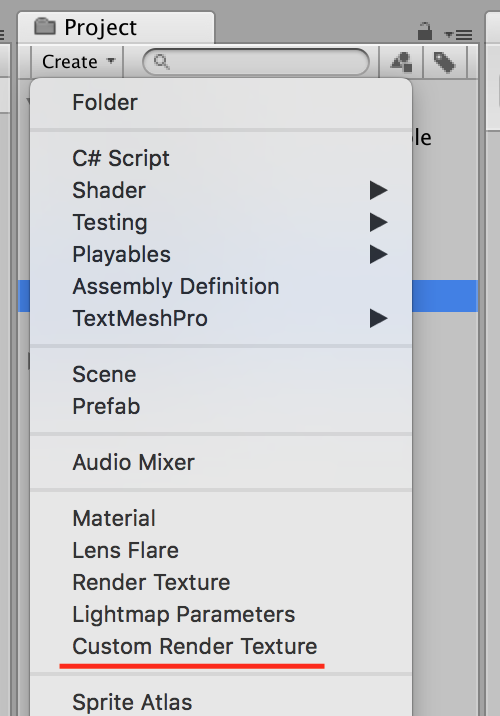
CustomRenderTexutreの設定
生成したCustomRenderTextureのインスペクタを見ると以下のような設定項目があります。
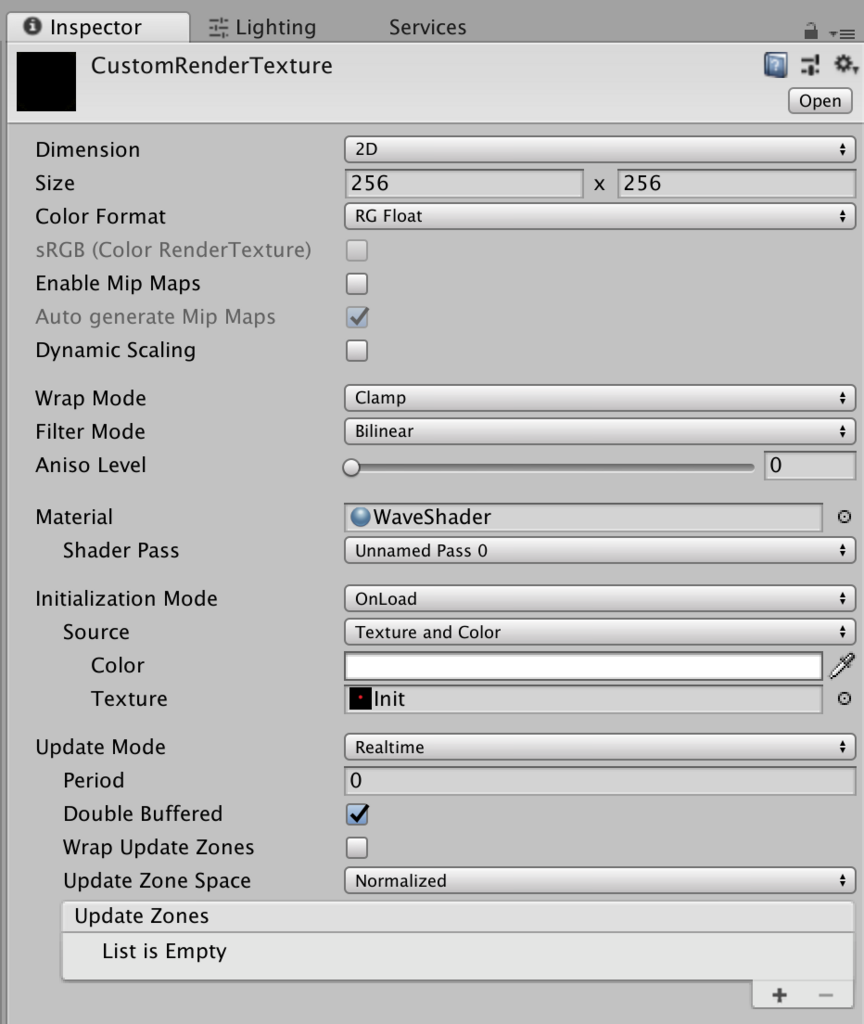
設定項目抜粋
いくつかの設定項目について見ていきます。
Size
CustomRenderTextureのサイズです。
Color Format
今回は凹みさんの記事にならって「RG Float」としています。
これは、現在の波の高さをR要素に、ひとつ前の波の高さをG要素に格納して計算を行うためです。
Material
CustomRenderTextureで使用するシェーダを適用したマテリアルを設定します。
サブ項目に「Shader Pass」がありますが、これは複数パスを定義した場合に、どのパスを利用するか選択できるようになっています。
Initialize Mode
初期化モード。OnLoadとすることで、起動時に初期化されます。
スクリプトから制御する場合は「OnDemand」を選択します。
サブ項目として「Source」があります。
設定できる内容は「Texture and Color」か「Material」があります。
今回は初期化をテクスチャから指定しています。
その場合は初期化に利用するテクスチャを設定する必要があります。
Update Mode
テクスチャの更新に関する設定です。
サンプルでは「Realtime」を設定しています。
こうすることで、スクリプトなしに自動的に更新が行われるようになります。
なお、スクリプトから制御したい場合はこちらも「OnDemand」を選択します。
Double Buffered
ダブルバッファのオン/オフ。
これをオンにすることで、テクスチャの情報をピンポンするように更新することができるようになります。
バンプマップに関して
以上でCustomRenderTextureに関する話はおしまいです。
今回の例ではシミュレーションした波形を利用してバンプマップを行っています。
ただ、シミュレーションした結果はRG要素しかない上に、それぞれのチャンネルはHeightMapとなっているためそのままでは法線マップとして利用できません。
そのため、取得したHeightMapから法線を計算して利用する必要があります。
バンプマップとは
法線マップを使ってポリゴンに凹凸があるように見せる処理です。
以前、Qiitaの記事にも書いたのでよかったら見てみてください。
なお、今回は法線をハイトマップから計算で求めて適用するための方法について書いていきます。
法線をハイトマップから計算で求める
ということで、法線の計算についても書いておきたいと思います。
法線の計算にあたっては、以下のふたつの記事を参考にさせていただきました。
法線は接ベクトルに垂直
接ベクトルをWikipediaで調べると以下のようにあります。
数学において、接ベクトル(英: tangent vector)とは、曲線や曲面に接するようなベクトルのことである。
そして、参考にさせていただいた記事(t-pot『動的法線マップ』)から説明を引用させていただくと、
法線ベクトルの求め方ですが、接ベクトルが法線ベクトルに直行することを利用します。 今回の場合は、高さ情報だけしか変化しないので、X軸及びZ軸の方向に関する高さの偏微分が接ベクトルの方向になります。
ということ。
つまり、接ベクトルをX軸およびZ軸に対して求め、それの外積を取ることで法線を求める、ということです。
図にすると以下のようなイメージです。
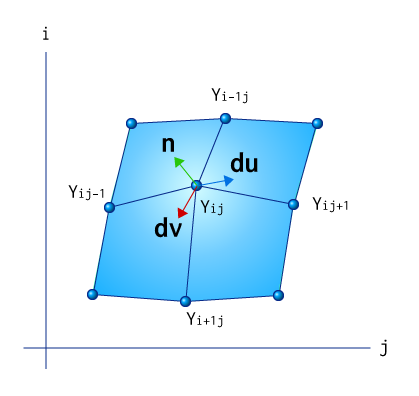
数式にすると以下のようになります。
よって、これを利用して以下のように法線を求めることができます。
float3 du = (1, dyx, 0) float3 dv = (0, dyz, 1) float3 n = normalize(cross(dv, du))
実装
コードにすると以下のようになります。(一部抜粋)
// _ParallaxMap_TexelSizeは、テクスチャサイズの逆数 // テクセルの「ひとつ隣(シフト)」分の値を計算する float2 shiftX = float2(_ParallaxMap_TexelSize.x, 0); float2 shiftZ = float2(0, _ParallaxMap_TexelSize.y); // 現在計算中のテクセルの上下左右の隣のテクセルを取得 float3 texX = tex2D(_ParallaxMap, float4(i.uv.xy + shiftX, 0, 0)) * 2.0 - 1; float3 texx = tex2D(_ParallaxMap, float4(i.uv.xy - shiftX, 0, 0)) * 2.0 - 1; float3 texZ = tex2D(_ParallaxMap, float4(i.uv.xy + shiftZ, 0, 0)) * 2.0 - 1; float3 texz = tex2D(_ParallaxMap, float4(i.uv.xy - shiftZ, 0, 0)) * 2.0 - 1; // 偏微分により接ベクトルを求める float3 du = float3(1, (texX.x - texx.x), 0); float3 dv = float3(0, (texZ.x - texz.x), 1); // 接ベクトルの外積によって「法線」を求める float3 n = normalize(cross(dv, du));
実装は難しい点はありません。
上下の高さ差分と、左右の高さ差分からそれぞれ勾配(接ベクトル)を求め、その2つのベクトルから外積を求めるだけです。
法線は接ベクトルと垂直なので、これで無事、法線が計算できたことになりますね。
最後に、バンプマップを行ったシェーダの全文を載せておきます。
Shader "Unlit/HightMapNormal"
{
Properties
{
_Color("Tint color", Color) = (1, 1, 1, 1)
_MainTex("Texture", 2D) = "white" {}
_ParallaxMap("Parallax Map", 2D) = "gray" {}
}
SubShader
{
Tags { "RenderType" = "Transparent" "Queue" = "Transparent" }
LOD 100
GrabPass { }
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
#include "Lighting.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float4 vertex : SV_POSITION;
float4 uvgrab : TEXCOORD1;
float3 worldPos : TEXCOORD2;
};
sampler2D _MainTex;
sampler2D _ParallaxMap;
sampler2D _GrabTexture;
float4 _MainTex_ST;
fixed4 _Color;
float2 _ParallaxMap_TexelSize;
v2f vert(appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.worldPos = mul(UNITY_MATRIX_MV, v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
#if UNITY_UV_STARTS_AT_TOP
float scale = -1.0;
#else
float scale = 1.0;
#endif
o.uvgrab.xy = (float2(o.vertex.x, o.vertex.y * scale) + o.vertex.w) * 0.5;
o.uvgrab.zw = o.vertex.zw;
return o;
}
fixed4 frag(v2f i) : SV_Target
{
float2 shiftX = float2(_ParallaxMap_TexelSize.x, 0);
float2 shiftZ = float2(0, _ParallaxMap_TexelSize.y);
float3 texX = tex2D(_ParallaxMap, float4(i.uv.xy + shiftX, 0, 0)) * 2.0 - 1;
float3 texx = tex2D(_ParallaxMap, float4(i.uv.xy - shiftX, 0, 0)) * 2.0 - 1;
float3 texZ = tex2D(_ParallaxMap, float4(i.uv.xy + shiftZ, 0, 0)) * 2.0 - 1;
float3 texz = tex2D(_ParallaxMap, float4(i.uv.xy - shiftZ, 0, 0)) * 2.0 - 1;
float3 du = float3(1, (texX.x - texx.x), 0);
float3 dv = float3(0, (texZ.x - texz.x), 1);
float3 n = normalize(cross(dv, du));
i.uvgrab.xy += n * i.uvgrab.z;
fixed4 col = tex2Dproj(_GrabTexture, UNITY_PROJ_COORD(i.uvgrab)) * _Color;
float3 lightDir = normalize(_WorldSpaceLightPos0 - i.worldPos);
float diff = max(0, dot(n, lightDir)) + 0.5;
col *= diff;
float3 viewDir = normalize(_WorldSpaceCameraPos - i.worldPos);
float NdotL = dot(n, lightDir);
float3 refDir = -lightDir + (2.0 * n * NdotL);
float spec = pow(max(0, dot(viewDir, refDir)), 10.0);
col += spec + unity_AmbientSky;
return col;
}
ENDCG
}
}
}
このシェーダのマテリアルを平面に適用することで、冒頭の動画の効果を得ることができます。
参考記事
その他、参考になった記事を載せておきます。
カールノイズを使ったパーティクル表現

概要
以前、カールノイズについてふたつの記事を書きました。
カールノイズの「流体表現」についてと「衝突判定」についてです。
今回はこれを発展させて、上記のカールノイズを使った具体的なパーティクル表現について書きたいと思います。
実際に動いている様子はこんな感じです↓
移動量に応じて自動でエミットするタイプ↓
自分たちで作っているコンテンツのキャラ(エルミナ)を格闘家っぽくするというコンセプトで作ってみた動画。カールノイズパーティクルを適用してみました。 pic.twitter.com/BfK2Xgdz4w
— edom18@VR (@edo_m18) 2018年7月16日
モデルの頂点位置からエミットするタイプ↓
ドラクエ11のリレミト風の演出を作ってみた pic.twitter.com/6J1kvenuUh
— edom18@VR (@edo_m18) 2018年7月25日
上の例では移動距離に応じて発生させるパーティクルと、メッシュの頂点部分にパーティクルを発生させる2パターンを実装しました。
なお、今回のサンプルはGithubにアップしてあります。
ちなみに、後者の「頂点部分にパーティクル」というのは、ドラクエ11のリレミトの表現をイメージしてみました↓
【ドラクエ11】目指せ最速クリア!ぶっ続けでプレイして世界を救う配信!【ネタバレ注意】
前回の実装ではパーティクルはすべて常にアップデートされていた
前の実装ではすべてのパーティクルが生きていて常に更新がかかる実装になっていました。
以前に投稿した動画はこんな感じです↓
やったー。カールノイズの衝突判定もちゃんと動いた。 pic.twitter.com/lMC8pgHjrc
— edom18@VR (@edo_m18) 2018年6月29日
見てもらうと分かりますがパーティクルが発生し続けていて「任意のタイミングで追加する」というケースがなかったわけですね。
つまりパーティクルは常に発生し続けライフタイムが0になったらまた新しく生成し直す、というサイクルで実装していました。
具体的には、ライフタイムがゼロになったらライフタイムを回復させ、位置を初期位置(ランダム性あり)として更新していました。
なので毎フレームパーティクルのデータを更新すればよく、休止中のパーティクルを起こす必要もなければ状態を管理する必要もなかったわけです。
しかし移動距離で発生させたりなど、「任意のタイミングで追加」する必要がある場合は「活動中」と「休止中」のパーティクルを管理し、追加の場合は休止中のパーティクルに対して処理を実行する必要が出てきます。
連続してパーティクルをエミットする
冒頭で紹介したパーティクル表現では(Unity標準のパーティクルシステムでも同様の機能がありますが)「移動した距離に応じてエミットする」という実装になっています。
つまり、前に発生させたパーティクルは維持しつつ、新しく追加でパーティクルを発生させる必要がある、というわけです。
パーティクルをプールして管理する
今回の実装ではパーティクルの状態を管理し、必要であれば追加でエミットする必要があることは書きました。
ではそれをどうやったら実現できるのでしょうか。
先に結論を書いてしまうと、休止しているパーティクルのIDを保持するバッファを用意し、休止になったパーティクルのIDはプールへ戻し、追加の必要が出た場合はそのプールからIDを取り出し利用する、という仕組みを作ります。
この実装にあたっては、凹みTipsの以下の記事を参考にさせていただきました。
まずはザッと今回新しく追加した処理を見てみます。
プールの状態を初期化するInitカーネル
Initカーネルで行っているのは、用意されたパーティクルバッファ分の初期化です。
処理はシンプルに、全パーティクルの非活性化およびそのIDのプールへの保存です。
////////////////////////////////////////////////////////////
///
/// 初期化処理のカーネル関数
///
[numthreads(8, 1, 1)]
void Init(uint id : SV_DispatchThreadID)
{
_Particles[id].active = false;
_DeadList.Append(id);
}
上記の_DeadList.Append(id);がプールへIDを保存している箇所ですね。
_DeadListの名前の通り、非活性化状態のパーティクルのIDを保存しているバッファです。
さて、このAppendを実行しているバッファはなんでしょうか。答えは以下です。
Append Buffer、Consume Bufferを利用してプールを管理する
Append BufferとConsume Bufferはそれぞれ、追加・取り出し可能なLIFO(Last In First Out)コンテナです。(つまり、最後に入れた要素が最初に取り出されるタイプのコンテナです)
MSDNのドキュメントは以下です。
AppendStructuredBufferのドキュメントから引用すると、
Output buffer that appears as a stream the shader may append to. Only structured buffers can take T types that are structures.
シェーダから追加することができるストリームとしてのバッファ、とあります。
このバッファに対して、寿命が来たパーティクルをバッファに入れてあげることで死活管理ができるというわけです。
ちなみにシェーダ内では以下のように定義しています。
AppendStructuredBuffer<uint> _DeadList; ConsumeStructuredBuffer<uint> _ParticlePool;
さて、ふたつのバッファを定義しているのでふたつのバッファを用意する必要があるのか、と思われるかもしれませんが、インターフェースが違うだけでバッファとしての実態は同じものを利用します。
CPU(C#)側での処理は以下のようになっています。
private ComputeBuffer _particlePoolBuffer; // --------------------- _particlePoolBuffer = new ComputeBuffer(_particleNumLimit, sizeof(int), ComputeBufferType.Append); // --------------------- _computeShader.SetBuffer(_curlnoiseKernel, _deadListId, _particlePoolBuffer); // --------------------- _computeShader.SetBuffer(_emitKernel, _particlePoolId, _particlePoolBuffer);
まず、ComputeBuffer型の_particlePoolBufferを定義し、タイプをComputeBufferType.Appendとしてバッファを生成しています。
その後SetBufferによってバッファをセットしていますが、見て分かる通り実際に渡しているバッファの参照はどちらも同じ_particlePoolBufferです。
つまり、追加する場合はAppendStructuredBufferとして参照を渡し、取り出すときはConsumeStructuredBufferとして参照を渡す、というわけですね。
これで、寿命が尽きたパーティクルはバッファ(リスト)に戻され、必要になったときに、非活性化しているパーティクルのIDを「取り出して」値を設定することで、今回のように追加でエミットできるようになる、というわけです。
パーティクルを追加でエミットする
さて、仕組みが分かったところで実際にエミットしているところを見てみましょう。
////////////////////////////////////////////////////////////
///
/// パーティクルをエミットさせるカーネル関数
///
[numthreads(8, 1, 1)]
void Emit()
{
uint id = _ParticlePool.Consume();
float2 seed = float2(id + 1, id + 2);
float3 randomPosition = rand3(seed);
Particle p = _Particles[id];
p.active = true;
p.position = _Position + (randomPosition * 0.05);
p.velocity = _Velocity;
p.color = _Color;
p.scale = _Scale;
p.baseScale = _BaseScale;
p.time = 0;
p.lifeTime = randRange(seed + 1, _MinLifeTime, _MaxLifeTime);
p.delay = _Delay;
_Particles[id] = p;
}
冒頭のuint id = _ParticlePool.Consume();がIDを取り出しているところですね。
こうして、非活性化しているパーティクルのIDを取り出し、取り出したパーティクルに対して新しくライフタイムや色、位置などを設定することで無事、該当のパーティクルが動き出す、というわけです。
パーティクルの死活管理
さて、パーティクル生成の最後に実際にパーティクルをアップデートしている箇所を見てみます。
前回の実装ではライフタイムがゼロになった場合はまた新しいライフタイムを即座に設定し、すぐに復活させていました。
が、今回は「非活性化状態リスト」に追加する必要があります。
該当の処理は以下になります。
////////////////////////////////////////////////////////////
///
/// カールノイズのカーネル関数
///
[numthreads(8, 1, 1)]
void CurlNoiseMain(uint id : SV_DispatchThreadID)
{
// ... 前略
if (p.active)
{
// ... 中略
if (p.time >= p.lifeTime)
{
p.active = false;
_DeadList.Append(id);
p.scale = 0;
}
}
// ... 後略
}
ライフタイムがゼロ以下になった場合は_DeadList.Append(id);として、非活性化リストに戻しているのが分かるかと思います。
これで晴れて、パーティクルの死活管理ができる、というわけです。
パーティクルの残り数を考慮する
以上でパーティクルを追加でエミットすることが可能になりました。
しかし今のままだと少し問題が残っています。
というのは、パーティクルの残数を管理する必要があることです。
パーティクルの計算にはComputeBufferによって渡されたパーティクル情報を元に計算を行います。
このとき、初期化のタイミングでパーティクル数を規定します。(バッファサイズを明示する必要があります)
サンプルでは30000という数字でバッファを生成しています。
つまり、(当然ですが)このサイズを超えるパーティクルは生成することができません。
しかし、今回の追加エミットの処理ではその上限を超えてパーティクルの追加を要求することができてしまいます。
当然、バッファサイズを超えた数をリクエストしてもプールには休止中のIDがなく、結果生成されることがありません。
自分が遭遇した問題としては、上限を超えてリクエストを行ってしまうとプールに戻るパーティクルがなくなり、結果的にパーティクルが再生されない、という問題がありました。
しかもその状態が発生してしまうと以後、まったくパーティクルが発生しなくなる、という問題に遭遇しました。
なので「上限を超えないように」エミットを調整しないとならない、というわけです。
現在のプールに残っているIDの数を取得する
ではどうするのか。
結論から先に書いてしまうと、プールに残っているIDの数を取得して調整を行います。
プールのカウントを取得するにはComputeBuffer.CopyCountを利用します。
取得、確認しているコードは以下です。
_particleArgsBuffer = new ComputeBuffer(1, sizeof(int), ComputeBufferType.IndirectArguments); _particleArgs = new int[] { 0 }; // -------------------- _particleArgsBuffer.SetData(_particleArgs); ComputeBuffer.CopyCount(_particlePoolBuffer, _particleArgsBuffer, 0); _particleArgsBuffer.GetData(_particleArgs); return _particleArgs[0];
最終的に_particleArgs のint型の配列に結果が格納されます。
今回のサンプルでは30000のパーティクルを生成しているので、まったくの未使用状態だと_particleArgs[0] == 30000となります。
MSDNのドキュメント↓
ComputeBuffer.CopyCount - Unity スクリプトリファレンス
あとは、ここで取得した数と実際にエミットしたい数とを比較すればバッファ以上のパーティクルを生成してしまうのを防ぐことができるようになります。
ジオメトリシェーダ入門
概要
今回はジオメトリシェーダ入門という形で記事を書いていきます。
頂点シェーダ、フラグメントシェーダに比べるとあまり書く機会の少ないシェーダ。
その2シェーダに比べて違いが結構あるのでそのあたりについてのメモを書いていこうと思います。
実際に使った例はこんな感じ↓

ジオメトリシェーダとは
Wikipediaによると以下のように説明されています。
ジオメトリシェーダー
ジオメトリシェーダー(英: Geometry Shader, GS)はピクセルシェーダーに渡されるオブジェクト内の頂点の集合を加工するために使用される。ジオメトリシェーダーにより、実行時に頂点数を増減させたり、プリミティブの種類を変更したりすることが可能となる。OpenGLではプリミティブシェーダーとも呼ばれる。ジオメトリシェーダーはポイント、ライン、トライアングルといった既存のプリミティブから新しいプリミティブを生成できる。
ジオメトリシェーダーは頂点シェーダーの後に実行され、プリミティブ全体または隣接したプリミティブの情報を持つプリミティブを入力する。例えばトライアングルを処理するとき、3つの頂点がジオメトリシェーダーの入力となる。ジオメトリシェーダーはラスタライズされるプリミティブを出力でき、そのフラグメントは最終的にピクセルシェーダーに渡される。またプリミティブを出力せずにキャンセルすることもできる。
ジオメトリシェーダーのよくある使い方としては、ポイントスプライトの生成、ジオメトリテセレーション、シャドウボリュームの切り出し、キューブマップあるいはテクスチャ配列へのシングルパスレンダリングなどがある。
ざっくりと要約すると、頂点単位ではなく、ポリゴン単位などで値を計算し、さらにはポリゴン枚数すら増やすことができるシェーダ、という感じでしょうか。
テッセレーションは分かりやすい使用例ですね。
その他の使い方としては、頂点郡からポリゴン(Quad)を生成しテクスチャを貼ることでパーティクルのような演出をする、なども使い道がありそうです。
まさにその発想で解説してくれている記事があるので紹介↓
コードを見てみる
さて、ジオメトリシェーダのシンプルなコードを見てみましょう。
下の例ではジオメトリシェーダではある意味で「なにもしていません」。
つまり、ポリゴンは変形しません。
が、ジオメトリシェーダがなにをしてくれているのかを見るのにちょうどいいと思います。
appdata vert(appdata v)
{
// ジオメトリシェーダで処理するため、頂点シェーダへの入力をそのまま返す
return v;
}
// ジオメトリシェーダでは3頂点のinputと3頂点のoutputを行う=つまり普通の三角ポリゴン
// max vertex count 3が3頂点のoutputであることを伝えている
// また、triangle appdata input[3]が、「三角形」で3頂点のinputが必要であることを伝えている
[maxvertexcount(3)]
void geom(triangle appdata input[3], inout TriangleStream<vsout> outStream)
{
[unroll]
for (int i = 0; i < 3; i++)
{
// 頂点シェーダからもらった3頂点それぞれを射影変換して通常のレンダリングと同様にポリゴン位置を決める
appdata v = input[i];
vsout o;
o.vertex = UnityObjectToClipPos(v.vertex);
outStream.Append(o);
}
outStream.RestartStrip();
}
fixed4 frag(vsout i) : SV_Target
{
return float4(1, 0, 0, 1);
}
頂点シェーダやフラグメントシェーダに比べるとやや特殊な感じになっています。
特に、関数に対してアトリビュートが指定されています。
細かな点についてはコメントで記載しました。
MSDNのドキュメント(ジオメトリ シェーダー オブジェクト (DirectX HLSL).aspx))を見ると以下のように書かれています。
ドキュメント
Syntax
[maxvertexcount(NumVerts)] void ShaderName ( PrimitiveType DataType Name [ NumElements ], inout StreamOutputObject );
パラメーター
- [maxvertexcount(NumVerts)]
- [in] 作成する頂点の最大数の宣言です。
- [maxvertexcount()] - 必須のキーワードです。正しい構文とするために、山かっこと丸かっこを必ず記述します。
- NumVerts - 頂点の数を表す整数です。
- [in] 作成する頂点の最大数の宣言です。
- ShaderName
- [in] ジオメトリ シェーダー関数の一意の名前を含む ASCII 文字列。
- PrimitiveType DataType Name [ NumElements ]
- PrimitiveType - プリミティブ型。プリミティブ データの順序を決定します。
- DataType - [in] 入力データ型。任意の HLSL データ型を指定できます。
- Name - ASCII 文字列の引数名。引数が配列の場合は、NumElements で配列サイズを任意に指定できます。
| プリミティブの種類 | 説明 |
|---|---|
| point | ポイント リスト |
| line | ライン リストまたはライン ストリップ |
| triangle | トライアングル リストまたはトライアングル ストリップ |
| lineadj | 隣接性のあるライン リストまたは隣接性のあるライン ストリップ |
| triangleadj | 隣接性のあるトライアングル リストまたは隣接性のあるトライアングル ストリップ |
- StreamOutputObject
- ストリーム出力オブジェクト.aspx)の宣言。
ストリーム出力オブジェクト
ここで、「ストリーム出力オブジェクト」は出力されるオブジェクトの種類に応じて指定するものが変わります。(例えばポリゴンとして出力するのか、ラインとして出力するのか、など)
ドキュメントから引用すると、以下の3つが定義されているようです。
Syntax
inout StreamOutputObject<DataType> Name;
パラメーター
- StreamOutputObject
Name - ストリーム出力オブジェクト (SO) 宣言
| ストリーム出力オブジェクトの型 | 説明 |
|---|---|
| PointStream | ポイント プリミティブのシーケンス |
| LineStream | ライン プリミティブのシーケンス |
| TriangleStream | トライアングル プリミティブのシーケンス |
違ったコードを見てみる
次に、ちょっとだけ違ったコードを見てみます。
これはポリゴン単位で法線を計算している例です。
通常の頂点シェーダでは頂点ごとの計算しかできないため、実際に生成されたポリゴンに対しての処理は書けません。
頂点だけではポリゴンを形成する「隣接する」他の頂点情報がないために計算が行えないためですね。
しかしジオメトリシェーダでは「ポリゴン単位」で処理が行えるため、こうしたことが可能になっています。
[maxvertexcount(3)]
void geom(triangle appdata input[3], inout TriangleStream<vsout> outStream)
{
float3 edge1 = (input[1].vertex.xyz - input[0].vertex.xyz);
float3 edge2 = (input[2].vertex.xyz - input[0].vertex.xyz);
float3 normal = normalize(cross(edge1, edge2));
[unroll]
for (int i = 0; i < 3; i++)
{
appdata v = input[i];
vsout o;
o.pos = UnityObjectToClipPos(v.vertex);
o.normal = normal;
outStream.Append(o);
}
outStream.RestartStrip();
}
上記の例では、ポリゴンのエッジから法線を計算しています。
こんな感じで「ポリゴン単位」で計算が行えるのが特徴です。
また上記で紹介した記事のように、inputの数とouputの数を変えることができるので、1枚のポリゴンから数枚のポリゴン、というようにポリゴン数を増やすことも可能です。
実例を見てみる
さて最後に、実際に利用されているシェーダを覗いてみて終わりにします。
以下の例は、凹みさんが書かれている「凹みTips」の記事(HoloLens で使える Near Clip 表現について解説してみた)で紹介されているものです。
本人の承諾をいただいて解説させていただいています。
※ 以下のコードは凹みさんが公開しているものを若干変更したものになります。
凹みさんが作った実際のものを動かすと以下のような感じになります。
(凹みさんの画像を引用させていただきました)

ジオメトリシェーダの部分だけ抜粋しました↓
ポイントを絞ってコード内にコメントを記載しています。
// 前のサンプル同様、3頂点のinput / outputが指定されています。
[maxvertexcount(3)]
void geom(triangle appdata_t input[3], inout TriangleStream<g2f> stream)
{
// ポリゴンの中心を計算。
// ポリゴン単位で計算を行えるため、「ポリゴンの中心位置」も計算可能です。
float3 center = (input[0].vertex + input[1].vertex + input[2].vertex) / 3;
// ポリゴンの辺ベクトルを計算し、ポリゴンの法線を計算する。
// 続いて、前のサンプルでもあった「ポリゴン法線」の計算です。
float3 vec1 = input[1].vertex - input[0].vertex;
float3 vec2 = input[2].vertex - input[0].vertex;
float3 normal = normalize(cross(vec1, vec2));
#ifdef _METHOD_PROPERTY
// カメラ視点を利用しない場合はパラメータをそのまま利用する
fixed destruction = _Destruction;
#else
// カメラ視点からの距離によって分解する場合は、中心位置をワールド座標に変換し、
// カメラとの距離を計算して係数に利用する
float4 worldPos = mul(Unity_ObjectToWorld, float4(center, 1.0));
float3 dist = length(_WorldSpaceCameraPos - worldPos);
fixed destruction = clamp((_StartDistance - dist) / (_StartDistance - _EndDistance), 0.0, 1.0);
#endif
// 省略していますが、独自で定義した「rand」関数を使って乱数を生成しています。
// ここではポリゴン位置などをseedにして乱数を生成しています。
fixed r = 2.0 * (rand(center.xy) - 0.5);
fixed3 r3 = r.xxx;
float3 up = float3(0, 1, 0);
// コードをループじゃない状態に展開することを明示する(詳細は下の記事を参照)
[unroll]
for (int i = 0; i < 3; i++)
{
appdata_t v = input[i];
g2f o;
UNITY_SETUP_INSTANCE_ID(v);
UNITY_INITIALIZE_VERTEX_OUTPUT_STEREO(o);
// 以下では、各要素(位置、回転、スケール)に対して係数に応じて変化を与えます。
// center位置を起点にスケールを変化させます。
v.vertex.xyz = (v.vertex.xyz - center) * (1.0 - destruction * _ScaleFactor) + center + (up * destruction);
// center位置を起点に、乱数を用いて回転を変化させます。
v.vertex.xyz = rotate(v.vertex.xyz - center, r3 * destruction * _RotationFactor) + center;
// 法線方向に位置を変化させます
v.vertex.xyz += normal * destruction * _PositionFactor * r3;
// 最後に、修正した頂点位置を射影変換しレンダリング用に変換します。
o.vertex = UnityObjectToClipPos(v.vertex);
#ifdef SOFTPARTICLES_ON
o.projPos = ComputeScreenPos(o.vertex);
COMPUTE_EYEDEPTH(o.projPos.z);
#endif
o.color = v.color;
o.color.a *= 1.0 - destruction * _AlphaFactor;
o.texcoord = TRANSFORM_TEX(v.texcoord, _MainTex);
UNITY_TRANSFER_FOG(o, o.vertex);
stream.Append(o);
}
stream.RestartStrip();
}
※ [unroll]については以下の記事がどうなるのか分かりやすいでしょう。
だいぶ駆け足ですが、ジオメトリシェーダの概要と実例を紹介しました。
最後の実例の詳細については凹みさんのブログ記事を参照してください。
ちなみにこうした動作を頂点シェーダで行ってしまうと、全頂点がむすばれてしまってトゲトゲした感じの見た目になるだけで、こうした動きは得られません。
凹みさんの記事には書いてありますが、ジオメトリシェーダに対応していないモバイルなどの環境では全頂点をポリゴン用に複製し、実際にポリゴンとして分解しておく必要があります。
こうした点でも、事前準備なしにこうした演出が行えるのはメリットですね。
実際に動いている動画
ちなみに以前投稿した以下の動画で動いているポリゴン分解は、凹みさんの記事を参考にさせてもらって実装したものです。SAO感が好きですw
前に作ったSAO風味のやつに、トラッカーにアタッチメントつけてプレイしたら「斬ってる感」が大幅に増したw pic.twitter.com/Ltzo38qZyT
— edom18@VR (@edo_m18) 2018年3月29日
OBB(Oriented Bounding Box)を計算する
概要
今回はOBB(Oriented Bounding Box)についてのまとめです。
今実装している中でボリュームのサイズをある程度正確に量りたいと思ったのが理由です。
今回の実装はこちらの記事を参考に、いくつかの記事を参照して行いました。
こちらの記事に書かれている手順を引用させていただくと以下のようになります。
- 頂点座標で行列を作る(xyz座標3データ×5000個のデータで3×5000の行列)
- xyz各行の平均を計算して引く
- 引いた行列の転置行列を作る(5000×3の行列)
- 掛けてNで割って共分散行列ができる((3×5000)×(5000×3)→3×3の行列)
- ヤコビ法などを用いて共分散行列の固有値・固有ベクトルを計算する
- 固有値と固有ベクトルが求まれば、固有値の大きい順に固有ベクトルを並べ替えます。
- 固有ベクトルを並べて3×3の行列を作っておきます。
- 固有ベクトルの行列と頂点の内積を計算し、各固有ベクトル毎に最大と最小の内積値を計算します。
- そのデータを使えば重心、OBBの座標が計算できます。(参考サイト参照)
ひとつひとつ見ていきましょう。
OBBとは
OBBとはOrientedと名前がついている通り、オブジェクトに対してできるだけ余白が出ないようにそれをすっぽりと覆うBoxを定義します。
それとは別にAABB(Axis Aligned Bounding Box)があります。Axis Alignedの名前の通り、座標空間のXYZ軸(Axis)に平行(Aligned)なBoxです。
つまり、オブジェクトが回転すると場合によっては無駄な余白ができてしまいます。
それぞれ図にすると以下のような感じの違いになります。

▲球体を半分にカットしてAABBを表示した状態

▲上記をOBBで表示した状態
いかがですか。オブジェクトの形状や回転状態によってだいぶ違いが出るのが分かるかと思います。
OBBの実装の概要についてはこちらの記事が参考になります。
記事から引用させていただくと、
簡単に言うと、あるポリゴン群に対してどんな方向を向いていてもかまわないので、それをすっぽりと囲む、できる限り小さな直方体を作りましょうというのがOBBの手法です。
この直方体をいかにして作るのかという所が腕の見せ所になります。
とりあえずここでは、上記論文で紹介されている主成分分析を使うことにしましょう。
と書かれています。
主成分分析とは
記事で書かれている主成分分析とはなんでしょうか。
Wikipediaによるとこう書かれています。
主成分分析(しゅせいぶんぶんせき、英: principal component analysis; PCA)とは、相関のある多数の変数から相関のない少数で全体のばらつきを最もよく表す主成分と呼ばれる変数を合成する多変量解析の一手法[1]。データの次元を削減するために用いられる。
主成分を与える変換は、第一主成分の分散を最大化し、続く主成分はそれまでに決定した主成分と直交するという拘束条件の下で分散を最大化するようにして選ばれる。主成分の分散を最大化することは、観測値の変化に対する説明能力を可能な限り主成分に持たせる目的で行われる。選ばれた主成分は互いに直交し、与えられた観測値のセットを線型結合として表すことができる。言い換えると、主成分は観測値のセットの直交基底となっている。主成分ベクトルの直交性は、主成分ベクトルが共分散行列(あるいは相関行列)の固有ベクトルになっており、共分散行列が実対称行列であることから導かれる。
なんだか分かったような分からないようなw
自分の理解としては、多数ある点群に対して方向性を見出し、それを計算によって求めた値を掛けることで分析しやすい形にする、といった感じでしょうか。
固有値・固有ベクトルとは
主成分分析には「固有値・固有ベクトル」を使って変換が行われるようです。
固有値、固有ベクトルについては以下の記事がとても分かりやすかったです。
なんだかどんどん主題と離れていっている気がしなくもないですが、まぁせっかくなのでまとめておきましょうw
上で紹介した記事を見てもらうとアニメーションで示してくれているのでとても分かりやすいですが、自分の理解として言葉で説明しておくと。
とあるベクトルに対して、とある行列を掛けたとき、そのベクトルが回転せず定数倍になるベクトルのことを「固有ベクトル」、そしてその定数倍の定数が「固有値」、ということのようです。
数式で表すと以下になります。
※ ただし
が行列で
が定数(スカラー)です。
行列での演算が定数(スカラー)の演算で表せる、というのが上記式の意味です。
(推測ですが)統計学や主成分分析に使える理由としては、傾向がある=回転しないベクトル(方向)、みたいなことから来ているんでしょうか。
ちょっと数学に疎いのでそのあたりの深い話は分かりません・・・。
閑話休題。
さて、最初に紹介した記事を読み進めると以下のように続いています。
OBBではデータとはポリゴンの頂点群なので、x,y,zの3次元のデータが頂点の個数分存在します。 それを使って分散共分散行列を作って、その行列の固有ベクトルを計算すると、 OBBを表す3つの軸が得られます。
さぁ、また新しい単語が出てきましたw
分散共分散行列とは
ここでもWikipediaから引用させてもらうと、
統計学と確率論において分散共分散行列(ぶんさんきょうぶんさんぎょうれつ、英: variance-covariance matrix)や共分散行列(きょうぶんさんぎょうれつ、英: covariance matrix)とは、ベクトルの要素間の共分散の行列である。これは、スカラー値をとる確率変数における分散の概念を、多次元に自然に拡張したものである。
と書かれています。
「分散」と「共分散」があり、それを合成した行列のためこう呼ばれるようです。
ちなみに、「分散共分散行列」については以下の記事がとても分かりやすかったです。
分散
まずは分散について。
これまたWikipedia)から引用すると、
確率論および統計学において、分散(ぶんさん、英: variance)は、確率変数の2次の中心化モーメントのこと。これは確率変数の分布が期待値からどれだけ散らばっているかを示す非負の値である[1]。
つまり、確率変数がどれだけ「分散」しているか、ということかな。
また、上で紹介した記事を見てみると、以下のように説明されています。
具体的には、分散は「(各データの平均値からの距離)の2乗の平均」。
分散は2乗であることに注意。単位をそろえるために、分散の平方根を取ったものが標準偏差。
標準偏差をσで表すと、分散はσ2で表される。
とのこと。なるほど。
ちなみに「標準偏差」については以下の記事が分かりやすかったです。
いわゆる「偏差値」とか、その類の話ですね。
二乗する辺りが「なるほど」と思わされます。
つまり、平均値からの距離を二乗することにより、大きく散らばっている(大きく分散している)場合ほど偏差が大きくなる、というわけです。(大きな値の二乗はより大きな数値になる)
そして完全に余談ですが、以前、「[数学] 最小二乗平面をプログラムで求める」という記事を書いていてそこでも似た話が出てくるので興味がある方は読んでみてください。
共分散
こちらもWikipediaから引用すると、
共分散(きょうぶんさん、covariance)は、2 組の対応するデータ間での、平均からの偏差の積の平均値である[1]。2 組の確率変数 X, Y の共分散 Cov(X, Y) は、E で期待値を表すことにして、 Cov(X, Y) = E[(X - E[X])(Y - E[Y])] で定義する。
上で、分かりやすいと紹介した記事を読んでの自分の理解を書くと、異なるデータに対して分散を計算し、どれくらい相関があるか、を計算したものが共分散かな、と思っています。
ちなみにその記事では以下のように例えています。非常に分かりやすい。
例えば、生徒の「数学の点数」と「英語の点数」がどのような関係にあるか知りたい。数学ができる生徒はやはり英語ができるのか?(正の相関)、それとも数学ができる生徒は英語が苦手なのか(負の相関)。
そこで、数学の点数(xの値)と英語の点数(yの値)という、2つのデータ群を考慮した分散を「共分散」と呼び、この共分散Sxyは次の式で表される。
※ は転置
つまり、XとYというふたつのデータがあった場合、上記式で求まるXとYの相関を見るのがXYの共分散となります。
さらにXとXの共分散が分散、ということのようです。
式にすると以下。
分散と共分散が分かりました。あとはこれを行列の形に合成すると「分散共分散行列」となります。
行列の形は以下のようになるようです。
OBBの話に戻すと、「頂点郡」というバラけたデータから、XYZという3要素がどれくらい相関しているか、を主成分分析によって求める、みたいなことなのかなーと想像しています。(あくまで想像)
さて、では実際にどうこの分散共分散行列を求めるかと言うと、冒頭の記事の引用を再掲すると以下のように書かれています。
- 頂点座標で行列を作る(xyz座標3データ×5000個のデータで3×5000の行列)
- xyz各行の平均を計算して引く
- 引いた行列の転置行列を作る(5000×3の行列)
- 掛けてNで割って共分散行列ができる((3×5000)×(5000×3)→3×3の行列)
分散共分散行列の意味の解説を元に見てみるとやっていることはまさに同じことですね。
そして冒頭の記事が参考にしている記事には以下のようなコードが示されています。
Vertex配列に頂点データが入っていて、配列の長さがSizeになります。
mは全頂点の平均値です。
float C11 = 0, C22 = 0, C33 = 0, C12 = 0, C13 = 0, C23 = 0;
for( int i = 0; i < Size; ++i ) {
C11 += ( Vertex[i].x - m.x ) * ( Vertex[i].x - m.x );
C22 += ( Vertex[i].y - m.y ) * ( Vertex[i].y - m.y );
C33 += ( Vertex[i].z - m.z ) * ( Vertex[i].z - m.z );
C12 += ( Vertex[i].x - m.x ) * ( Vertex[i].y - m.y );
C13 += ( Vertex[i].x - m.x ) * ( Vertex[i].z - m.z );
C23 += ( Vertex[i].y - m.y ) * ( Vertex[i].z - m.z );
}
C11 /= Size;
C22 /= Size;
C33 /= Size;
C12 /= Size;
C13 /= Size;
C23 /= Size;
float Matrix[3][3] = {
{ C11, C12, C13 },
{ C12, C22, C23 },
{ C13, C23, C33 },
};
平均からの距離を求めて、それを行列にしている部分ですね。
ただ、いくつかの行列要素は同じ計算結果になるため必要な部分だけを計算して行列にしているのが分かります。
これで「分散共分散行列」を求めることができます。
次にここから「固有ベクトル」を求め、OBBの軸を求めます。
なお、コードを紹介してくれた記事では以下のように続いています。
こうして得られる分散共分散行列ことMatrix[3][3]は、
実対称行列なのでjacobi法で固有ベクトルを求めることができます。
固有ベクトルを求める
さて、だいぶ遠回りしてしまいましたが、ふんわりと、どういう処理を用いてOBBを計算するのかを見てきました。
最後に、求めたいのはOBBの軸と長さです。
3軸の向きと長さが分かればそこからOBBを求めることができますね。
ということで固有ベクトルを求める計算です。
jacobi法(ヤコビ法)で固有ベクトルを求める
前述の通り、分散共分散行列を求め、そこからjacobi法(ヤコビ法)という手法を用いて固有ベクトルを求めます。
jacobi法についてはこちらの記事(Jacobi法 - [物理のかぎしっぽ])を参考にさせていただきました。
該当記事の冒頭の解説を引用させてもらうと、
Jacobi法(ヤコビ法)を用いて行列の固有値と固有ベクトルを求めてみたいと思います. Jacobi法では対称行列しか扱えないという制約があるものの,アルゴリズム自体も簡単な上に,解が必ず実数になる事もあり,大変シンプルです.
とあります。
そして分散共分散行列は対称行列のためこの方法が使える、というわけのようです。
さて、実際の求め方ですが、引用させていただくと、
となるとき,行列Aと行列Bの固有値は一致します.また,行列Aが対称行列である場合,直交行列Pを用いて
と,対角化することができ,行列Λの対角成分は行列Λの固有値となります.ここで直交行列Pの列ベクトルとそれに対応する行列Λの列の対角成分は固有値と固有ベクトルの関係となります.このことから行列Aの固有値と固有ベクトルを求めるには,行列Aを対角化する直交行列Pを求めれば良いことになります.
Jacobi法ではこの直交行列Pを反復作業で求めています.つまり,行列Aの非対角成分の1つをゼロにする直交行列を用い,
とする事を繰り返します.[tex: P^{-1}n … P^{-1}4 P^{-1}3 P^{-1}2 P^{-1}_1 AP_1 P_2 P_3 P_4 … P_n = \Lambda]
これを繰り返し全ての非対角成分をゼロにし,対角化をするのがJacobi法です.また,
この部分が行列Aを対角化する直交行列であり,列ベクトルは固有ベクトルとなります.
上記の説明の中で出てくる式や単語を整理しておきます。
「直交行列」ですが、意味は逆行列と転置行列が等しくなる正方行列のことです。以下を満たす行列ですね。
また「対角化」を調べてみると以下の記事が分かりやすいです。
記事から説明を引用すると、
与えられた正方行列 A に対して,正則行列 P をうまく取ってきて
を対角行列にする操作を対角化と言う。
ヤコビ法で語られていた以下の式が出てきました。
ここで「正則行列Pをうまく取ってきて」とあります。
つまりこの「うまく取ってくる」というのがヤコビ法、ということになりますね。
さて実際のヤコビ法の計算方法ですが、詳細は紹介した記事を読んでみてください。
プログラムでの計算方法も掲載されています。
今回はそのプログラムコードを参考にさせていただき、Unity上で使えるようにC#で書き直しました。
C#コード
最後に、実際に書いたコードを掲載しておきます。よかったら参考にしてみてください。
以下のコードを貼り付けて実行すると、下図のようにOBBが表示されます。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class OBBTest : MonoBehaviour
{
private float _max = 0.0001f;
private Vector3[] _edges = new Vector3[0];
private Vector3 _origin;
private void OnDrawGizmos()
{
if (_edges.Length == 0)
{
return;
}
Gizmos.color = Color.yellow;
Gizmos.DrawWireSphere(_origin, 0.01f);
Gizmos.color = Color.blue;
Vector3 from, to;
Vector3 ftr = _origin + (_edges[0] * 0.5f) + (_edges[1] * 0.5f) + (_edges[2] * 0.5f);
Vector3 fbr = ftr - _edges[2];
Vector3 ftl = ftr - _edges[0];
Vector3 fbl = ftl - _edges[2];
Vector3 btr = ftr - _edges[1];
Vector3 bbr = btr - _edges[2];
Vector3 btl = btr - _edges[0];
Vector3 bbl = btl - _edges[2];
Gizmos.DrawLine(ftr, fbr);
Gizmos.DrawLine(ftr, ftl);
Gizmos.DrawLine(ftl, fbl);
Gizmos.DrawLine(fbl, fbr);
Gizmos.DrawLine(btr, bbr);
Gizmos.DrawLine(btr, btl);
Gizmos.DrawLine(btl, bbl);
Gizmos.DrawLine(bbl, bbr);
Gizmos.DrawLine(ftr, btr);
Gizmos.DrawLine(ftl, btl);
Gizmos.DrawLine(fbr, bbr);
Gizmos.DrawLine(fbl, bbl);
}
private void Awake()
{
CalcEdges();
}
private void Update()
{
if (Input.GetKeyDown(KeyCode.U))
{
CalcEdges();
}
}
private void CalcEdges()
{
MeshFilter filter = GetComponent();
Vector3[] vertices = filter.mesh.vertices;
float[,] eigenVectors = GetEigenVectors(CollectMatrix(vertices));
int rank = eigenVectors.Rank;
Vector3 vec1, vec2, vec3;
{
float x = eigenVectors[0, 0];
float y = eigenVectors[1, 0];
float z = eigenVectors[2, 0];
vec1 = new Vector3(x, y, z);
}
{
float x = eigenVectors[0, 1];
float y = eigenVectors[1, 1];
float z = eigenVectors[2, 1];
vec2 = new Vector3(x, y, z);
}
{
float x = eigenVectors[0, 2];
float y = eigenVectors[1, 2];
float z = eigenVectors[2, 2];
vec3 = new Vector3(x, y, z);
}
// 全頂点に対して内積を取り、最小値・最大値を計算する
float min1 = float.MaxValue;
float min2 = float.MaxValue;
float min3 = float.MaxValue;
float max1 = float.MinValue;
float max2 = float.MinValue;
float max3 = float.MinValue;
for (int i = 0; i < vertices.Length; i++)
{
Vector3 pos = vertices[i];
float dot1 = Vector3.Dot(vec1, pos);
if (dot1 > max1)
{
max1 = dot1;
}
if (dot1 < min1)
{
min1 = dot1;
}
float dot2 = Vector3.Dot(vec2, pos);
if (dot2 > max2)
{
max2 = dot2;
}
if (dot2 < min2)
{
min2 = dot2;
}
float dot3 = Vector3.Dot(vec3, pos);
if (dot3 > max3)
{
max3 = dot3;
}
if (dot3 < min3)
{
min3 = dot3;
}
}
float len1 = max1 - min1;
float len2 = max2 - min2;
float len3 = max3 - min3;
Vector3 edge1 = transform.localToWorldMatrix.MultiplyVector(vec1 * len1);
Vector3 edge2 = transform.localToWorldMatrix.MultiplyVector(vec2 * len2);
Vector3 edge3 = transform.localToWorldMatrix.MultiplyVector(vec3 * len3);
_edges = new[]
{
edge1, edge2, edge3,
};
Vector3 center1 = (vec1 * (max1 + min1)) * 0.5f;
Vector3 center2 = (vec2 * (max2 + min2)) * 0.5f;
Vector3 center3 = (vec3 * (max3 + min3)) * 0.5f;
_origin = transform.localToWorldMatrix.MultiplyPoint(center1 + center2 + center3);
}
private float[,] CollectMatrix(Vector3[] vertices)
{
// 各成分の平均を計算
Vector3 m = Vector3.zero;
for (int i = 0; i < vertices.Length; i++)
{
m += vertices[i];
}
m /= vertices.Length;
float c11 = 0; float c22 = 0; float c33 = 0;
float c12 = 0; float c13 = 0; float c23 = 0;
for (int i = 0; i < vertices.Length; i++)
{
c11 += (vertices[i].x - m.x) * (vertices[i].x - m.x);
c22 += (vertices[i].y - m.y) * (vertices[i].y - m.y);
c33 += (vertices[i].z - m.z) * (vertices[i].z - m.z);
c12 += (vertices[i].x - m.x) * (vertices[i].y - m.y);
c13 += (vertices[i].x - m.x) * (vertices[i].z - m.z);
c23 += (vertices[i].y - m.y) * (vertices[i].z - m.z);
}
c11 /= vertices.Length;
c22 /= vertices.Length;
c33 /= vertices.Length;
c12 /= vertices.Length;
c13 /= vertices.Length;
c23 /= vertices.Length;
float[,] matrix = new float[,]
{
{ c11, c12, c13 },
{ c12, c22, c23 },
{ c13, c23, c33 },
};
return matrix;
}
///
/// 行列の中の絶対値の最大値とその位置を返す
///
/// 評価する行列
/// 最大値の行位置
/// 最大値の列位置
/// 最大値
private float GetMaxValue(float[,] matrix, out int p, out int q)
{
p = 0;
q = 0;
int rank = matrix.Rank;
float max = float.MinValue;
for (int i = 0; i < rank; i++)
{
int len = matrix.GetLength(i);
for (int j = 0; j < len; j++)
{
// 対角成分は評価しない
if (i == j)
{
continue;
}
float absmax = Mathf.Abs(matrix[i, j]);
if (max <= absmax)
{
max = absmax;
p = i;
q = j;
}
}
}
if (p > q)
{
int temp = p;
p = q;
q = temp;
}
return max;
}
///
/// 固有ベクトルを得る
///
/// 評価する行列
private float[,] GetEigenVectors(float[,] matrix)
{
// 固有ベクトルのための行列を正規化
float[,] eigenVectors = new float[3,3];
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
if (i == j)
{
eigenVectors[i,j] = 1f;
}
else
{
eigenVectors[i,j] = 0;
}
}
}
int limit = 100;
int count = 0;
int p, q;
while (true)
{
count++;
if (count >= limit)
{
Debug.Log("somothing was wrong.");
break;
}
float max = GetMaxValue(matrix, out p, out q);
if (max <= _max)
{
break;
}
float app = matrix[p, p];
float apq = matrix[p, q];
float aqq = matrix[q, q];
float alpha = (app - aqq) / 2f;
float beta = -apq;
float gamma = Mathf.Abs(alpha) / Mathf.Sqrt(alpha * alpha + beta * beta);
float sin = Mathf.Sqrt((1f - gamma) / 2f);
float cos = Mathf.Sqrt((1f + gamma) / 2f);
if (alpha * beta < 0)
{
sin = -sin;
}
for (int i = 0; i < 3; i++)
{
float temp = cos * matrix[p, i] - sin * matrix[q, i];
matrix[q, i] = sin * matrix[p, i] + cos * matrix[q, i];
matrix[p, i] = temp;
}
for (int i = 0; i < 3; i++)
{
matrix[i, p] = matrix[p, i];
matrix[i, q] = matrix[q, i];
}
matrix[p, p] = cos * cos * app + sin * sin * aqq - 2 * sin * cos * apq;
matrix[p, q] = sin * cos * (app - aqq) + (cos * cos - sin * sin) * apq;
matrix[q, p] = sin * cos * (app - aqq) + (cos * cos - sin * sin) * apq;
matrix[q, q] = sin * sin * app + cos * cos * aqq + 2 * sin * cos * apq;
for (int i = 0; i < 3; i++)
{
float temp = cos * eigenVectors[i, p] - sin * eigenVectors[i, q];
eigenVectors[i, + q] = sin * eigenVectors[i, p] + cos * eigenVectors[i, q];
eigenVectors[i, + p] = temp;
}
}
return eigenVectors;
}
}
クォータニオン(回転)についてメモ
概要
Unityなどのゲームエンジンや、3D関連を扱っていると頻繁に出てくるクォータニオン。
しかしオイラー角に比べると各要素の意味が分かりづらく、直にクォータニオンをいじるケースはあまり多くないと思います。
しかし、少し凝ったことをしようとしたり、あるいはUnityにない機能を実装しようとした場合、クォータニオンを理解していないと困ることがあります。
ということで、今回はクォータニオンについてのちょっとした整理とTipsなどを書いていきたいと思います。
クォータニオンとは
Wikipediaから引用させてもらうと、
数学における四元数(しげんすう、英: quaternion(クォターニオン))は複素数を拡張した数体系である。四元数についての最初の記述は、1843年にアイルランドの数学者ウィリアム・ローワン・ハミルトンによってなされ[1][2]、三次元空間の力学に応用された。四元数の特徴は、二つの四元数の積が非可換となることである。ハミルトンは、四元数を三次元空間内の二つの有向直線の商として定義した[3]。これは二つのベクトルの商と言っても同じである[4]。四元数をスカラーと三次元のベクトルとの和として表すこともできる。
と記載があります。
(ちなみにクォータニオンは「四元数」とも言われます。内容的には4次元ベクトルの形だからでしょうか)
正直なんのこっちゃですが、(逆に「そうそう」って思える人はこの記事を読んでないでしょうw) 要はクォータニオンを使うことで3次元空間のベクトルの回転が行える、ということです。
またクォータニオンには行列のように積が非可換である、という点も挙げられます。
が、Unityで使っている上ではそこは気にしなくて大丈夫です。
Unity側でよしなにしてくれるので。
クォータニオンについての詳細は以下の記事がとても有用です。
記事には数式がたくさん出てきて、さらにそれらを巧みに変換しながら美しく解説していくので正直まだ全然理解できていませんが、雰囲気を掴むにはいいと思います。
クォータニオンの各要素
クォータニオンは4次元ベクトルの体をなしているので、(x, y, z, w)の4成分からなります。
ただ、オイラー角のように各成分にそれぞれの回転が格納されているわけではありません。
じゃあなにが入っているか、というと以下のような計算結果が格納されています。
- axis = 回転軸
- theta = 回転角
とした場合に、以下の計算結果が格納されている。
なのでx要素だけを取り出しても、軸の値と\(sin\)の値の合成なのでそれがどんな意味があるのかは分からない、というわけです。
クォータニオンTips
さてここからは、Unityなど実際の開発に使えるちょっとしたTips、覚えておくと幸せになれるかもしれないものをつらつらと書いていきます。
内積
3次元ベクトルと同様、クォータニオンにも内積が定義されています。
Quaternion q1 = /* any quartenion */ Quaternion q2 = /* any quartenion */ float cos = q1.x * q2.x + q1.y * q2.y + q1.z * q2.z + q1.w * q2.w; float angle = Mathf.Acos(cos) * Mathf.Rad2Deg;
上記のように、内積は3次元ベクトルと同様、ふたつのクォータニオンが成す角度\(\cos(\theta)\)となります。
UnityのAPIにもQuaternion.Dot(q1, q2)というメソッドが用意されています。
回転軸
先述した通り、クォータニオンは正規化した回転軸の各要素と\(sin\bigl(\frac{\theta}{2}\bigr)\)との掛け算により計算されます。
ただ、掛ける値は\(x, y, z\)各要素とも同じ値なので、これを正規化すれば回転軸のベクトルを得ることができます。
また、クォータニオンの各要素を考えると\(sin\bigl(\frac{\theta}{2}\bigr)\)と同じ値が得られれば、それで割ることで回転軸の値を得ることもできます。
// 2通りの方法で回転軸を計算する
private void ShowRotationAxis()
{
Quaternion q = transform.rotation;
Vector3 axis1 = new Vector3(q.x, q.y, q.z);
axis1.Normalize();
// 以下のようにsinの値で割っても同じ結果がられる
Vector3 axis2 = new Vector3(q.x, q.y, q.z);
float theta = Mathf.Acos(q.w);
float sin = Mathf.Sin(theta);
axis2.x /= sin;
axis2.y /= sin;
axis2.z /= sin;
Debug.LogFormat("x1: {0}", axis1.x);
Debug.LogFormat("y1: {0}", axis1.y);
Debug.LogFormat("z1: {0}", axis1.z);
Debug.LogFormat("x2: {0}", axis2.x);
Debug.LogFormat("y2: {0}", axis2.y);
Debug.LogFormat("z2: {0}", axis2.z);
}
ワールド空間での回転クォータニオンをローカル空間に変換する
あまり実用性はないかもしれませんが、ワールド空間で表されているクォータニオンを、ローカル空間でのクォータニオンに変換する処理です。
transform.rotation = q;とすると決まる回転を、transform.localRotation = q;として設定できるようにするイメージです。
private Quaternion ConvertToLocal(Quaternion q)
{
Quaternion result = Quaternion.identity;
Transform current = transform.parent;
while (current != null)
{
result *= Quaternion.Inverse(current.localRotation);
current = current.parent;
}
return result * q;
}
考え方はシンプルに、親のlocalRotationの逆クォータニオンを合算して戻します。
クォータニオンは掛ける順番が変わると結果が変わるので注意が必要です。
クォータニオンのSlerp
クォータニオンにもベクトル同様、LerpとSlerpという補間処理があります。
そしてSlerpの意味は「球面線形補間」です。
基本的にはUnity APIにすでにあるのでそれを利用するのがいいと思いますが、どういう処理がされているのかを把握しておくことは大事でしょう。
※ ちなみに余談ですが、今回の実装では補間するweightを0〜1に限定していないので、マイナス値や1以上の値を指定することができます。UnityのAPIでは0〜1の間に限定しているので、それを超えた補間(といっていいか分かりませんがw)をする場合は独自で実装する必要があります。
ということでSlerp処理のアルゴリズムです。
計算のアルゴリズム自体はこちらのC++実装(slerp.cpp - Sony CSL)を参考にしました。
また、いつもお世話になっているマルペケさんの記事にとても分かりやすい解説があるので合わせて読んでみるといいと思います。
Slerp処理の手順を先に書いておくと、
- ふたつのクォータニオンの回転差分を計算する
- 補間の係数(tと1-tのふたつ)を元に、(1)で計算した角度の比率として係数を掛けた値を計算する
- (2)で求めた値を\(\sin(\theta)\)で割る
- (3)で求めた値を係数として、ふたつのクォータニオンを合成する
という流れです。
まずは以下の図を見てください。

上図はふたつのベクトルを球面上で線形に補間する様子を示しています。
まず、StartからEndに向かってベクトルが補間されていきます。
その補間の度合いを決めるのが媒介変数\(t\)です。
そしてふたつのベクトルが成す角が\(\theta\)です。
球面線形補間を行うということは、ふたつのベクトル間を等速の角速度で移動する必要があります。
つまり、媒介変数\(t\)を利用すると\(t\theta\)で値が変化していけばいいわけです。
このとき、\(t\)の位置に向かうベクトルはふたつのベクトルの合成で表すことができます。
具体的にはStartベクトルとEndベクトルに平行なベクトルです。
図では黒い矢印になっている部分ですね。
さて、ではそのベクトルの長さはどう求めたらいいでしょうか。
ここで、三角形の比率の話を思い出すと、縦軸に書かれている\(\sin(\theta)\)と\(\sin(\theta(1-t))\)の比率がそのままStartに向かうベクトルと\(t\)の位置のベクトルとの比率になるのが分かるかと思います。
そしてStartベクトルは単位ベクトルなので長さは1です。
また求めたいベクトルを仮に\(V(t)\)と置くと、
「薄い緑のベクトル(1) : 濃い緑のベクトル(\(V(t)\))」の比率は「\(\sin(\theta)\) : \(\sin(\theta(1-t))\)」という比率になります。
これを整理すると以下のようになります。
以上を踏まえて以下の実装を見てみると、\(t\theta\)と\((1-t)\theta\)で係数を計算して、それぞれのクォータニオンを合成しているのが分かるかと思います。
////// Quaternion's slerp /// /// Refer: https://www.sonycsl.co.jp/person/nielsen/visualcomputing/programs/slerp.cpp /// /// Start Quaternion /// End Quaternion /// Weight ///Mixed quaternion by weight. static public Quaternion Slerp(Quaternion a, Quaternion b, float t) { float dot = Quaternion.Dot(a, b); float theta = Mathf.Acos(dot); if (theta < 0.0) { theta = -theta; } float st = Mathf.Sin(theta); if (st == 0) { return a; } float sut = Mathf.Sin(theta * t); float sout = Mathf.Sin(theta * (1f - t)); float coeff1 = sout / st; float coeff2 = sut / st; float x = coeff1 * a.x + coeff2 * b.x; float y = coeff1 * a.y + coeff2 * b.y; float z = coeff1 * a.z + coeff2 * b.z; float w = coeff1 * a.w + coeff2 * b.w; return new Quaternion(x, y, z, w); }
オイラー角からクォータニオンを求める
ちょっとしたメモということで、今度はオイラー角からクォータニオンを求めることをやってみようと思います。
計算式についてはWikipediaに記載があるので引用させてもらうと、
という計算を行うことで求めることができます。
ここで最初のベクトルの計算は、オイラー角なのでXYZ軸が回転していない通常の座標空間において、XYZ軸それぞれの回転を合成したクォータニオン、と見ることができます。
なので、上記の合成では「ZYX」の順で合成していることになりますね。
ただこの合成の順番は特に決まりがあるわけではなく、エンジンごとにどういう順番で掛けるのか、を決めておく必要があります。
調べたところ、Unityでは「YXZ」の順で掛けているようです。
※ 余談ですが、Three.jsの実装を見てみると、オーダーを指定できるようになっており、そこから色々試したところ「YXZ」が同じ結果になりました。
それらを踏まえて、実際のC#コードは以下のようになります。
mary> /// Convert euler to quaternion /// /// Euler's x /// Euler's y /// Euler's z ///Quternion from euler angles. static public Quaternion Euler(float x, float y, float z) { x *= Mathf.Deg2Rad; y *= Mathf.Deg2Rad; z *= Mathf.Deg2Rad; float c1 = Mathf.Cos(x * 0.5f); float c2 = Mathf.Cos(y * 0.5f); float c3 = Mathf.Cos(z * 0.5f); float s1 = Mathf.Sin(x * 0.5f); float s2 = Mathf.Sin(y * 0.5f); float s3 = Mathf.Sin(z * 0.5f); // Unity's order is 'YXZ' float qx = s1 * c2 * c3 + c1 * s2 * s3; float qy = c1 * s2 * c3 - s1 * c2 * s3; float qz = c1 * c2 * s3 - s1 * s2 * c3; float qw = c1 * c2 * c3 + s1 * s2 * s3; // 'ZXY' // float qx = s1 * c2 * c3 - c1 * s2 * s3; // float qy = c1 * s2 * c3 + s1 * c2 * s3; // float qz = c1 * c2 * s3 + s1 * s2 * c3; // float qw = c1 * c2 * c3 - s1 * s2 * s3; // 'XYZ' // float qx = s1 * c2 * c3 + c1 * s2 * s3; // float qy = c1 * s2 * c3 - s1 * c2 * s3; // float qz = c1 * c2 * s3 + s1 * s2 * c3; // float qw = c1 * c2 * c3 - s1 * s2 * s3; // 'ZYX' // float qx = s1 * c2 * c3 - c1 * s2 * s3; // float qy = c1 * s2 * c3 + s1 * c2 * s3; // float qz = c1 * c2 * s3 - s1 * s2 * c3; // float qw = c1 * c2 * c3 + s1 * s2 * s3; // 'YZX' // float qx = s1 * c2 * c3 + c1 * s2 * s3; // float qy = c1 * s2 * c3 + s1 * c2 * s3; // float qz = c1 * c2 * s3 - s1 * s2 * c3; // float qw = c1 * c2 * c3 - s1 * s2 * s3; // 'XZY' // float qx = s1 * c2 * c3 - c1 * s2 * s3; // float qy = c1 * s2 * c3 - s1 * c2 * s3; // float qz = c1 * c2 * s3 + s1 * s2 * c3; // float qw = c1 * c2 * c3 + s1 * s2 * s3; return new Quaternion(qx, qy, qz, qw); }
クォータニオンからオイラー角を求める
さて最後に、逆のクォータニオンからオイラー角を求める計算・・なのですが、それについては以前Qiitaで書いたのでそちらを参照ください。
回転の方向
クォータニオンを利用して回転を制御していると、たまに意図しない方向に回転することがあるかもしれません。特にアニメーションなどをしていると、思っている方向と逆に回る、など。
その答えは、安原さんのこちらのスライドのP.111あたりを見ると分かります。
www.slideshare.net
クォータニオンのすべての要素を反転(マイナスを掛ける)と、最終的な姿勢は同じでも回転方向が異なるということです。なので、スライドでは w の要素をチェックし、マイナスだった場合は全体を反転させる、という方法で回転を制御しています。
回転に困った場合はこのあたりを考えてみると解決するかもしれません。
最後に
クォータニオン、奥が深いですね。
Unityなどで利用する限りにおいては基本的にエンジン側で色々よしなにしてくれるので気にすることはありませんが、だいぶ複雑なことをやってくれているんだなーと実感させられます。
PlayerPrefsを操作するエディタウィンドウを作成する
概要
EditorWindowを継承した、エディタ拡張のメモです。
普段、エディタ作成をそんなにしていないので忘れがちなので。
ちなみに今回は、汎用的になるようにPlayerPrefsを操作するっていう名目でサンプルを作成しました。
準備
エディタ拡張の詳細はここでは触れません。
ここではEditorWindowクラスを継承して、ウィンドウタイプのエディタ拡張を制作するまでを書きます。
まず、UnityEditor.EditorWindowクラスを継承したクラスを作成します。
ウィンドウのインスタンスは初回のみ生成するようにしています。
ウィンドウの生成にはCreateInstance<T>();スタティックメソッドを利用します。
メニューから生成されるには以下のようにします。
public class PlayerPrefsEditor : EditorWindow { static private PlayerPrefsEditor _window; [MenuItem("Window/PlayerPrefsEditor")] static private void Open() { if (_window == null) { _window = CreateInstance<PlayerPrefsEditor>(); } } }
メニューには以下のように表示され、これを実行するとウィンドウが開きます。
ウィンドウの描画処理
ウィンドウが生成されると、インスペクタのエディタ拡張などと同じくOnGUIメソッドが定期的に呼ばれるようになります。
そこに、ボタンやラベルなどを表示させ、インタラクションさせることによってエディタを実装します。
private void OnGUI() { EditorGUILayout.LabelField("---- PlayerPrefs List ----"); }
この中に様々な処理を書けばリッチなエディタを作ることができます。
今回は実際に使用した部分だけをメモとして残しておきます。
スクロールビューを作る
項目が増えてくるとスクロールしないと収まらなくなってきます。
そんなときはスクロールビューを実装します。
スクロールビューにしたい箇所をGUILayout.BeginScrollView()とGUILayout.EndScrollView()ではさみます。
具体的には以下のようにします。
private Vector2 _scrollPos; private void OnGUI() { _scrollPos = GUILayout.BeginScrollView(_scrollPos, GUI.skin.box); // ... do anything. GUILayout.EndScrollView(); }
_scrollPosは現在のスクロール状態を保持するためにインスタンス変数として保持しておきます。
項目を枠でグルーピングする
また、項目が増えてくると各項目ごとにグルーピングしたくなってきます。
その場合はスクロールビューと似た感じでEditorGUILayout.BeginVertical()とEditorGUILayout.EndVertical()のメソッドで項目をはさみます。
private void OnGUI() { EditorGUILayout.BeginVertical(GUI.skin.box, GUILayout.ExpandWidth(true)); // ... do anything. EditorGUILayout.EndVertical(); }
最後に、最近のプロジェクトで使ったやつを一部を伏せつつ載せておきます。
using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEditor; using ElminaAR.Systems; public class PlayerPrefsEditor : EditorWindow { static private PlayerPrefsEditor _window; static private readonly string _userDataFoldoutKey = "UserDataFoldoutKey"; private Vector2 _scrollPos; private bool _isFirst; [MenuItem("Window/PlayerPrefsEditor")] static private void Open() { if (_window == null) { _window = CreateInstance<PlayerPrefsEditor>(); } #region ### Player Config ### _window._isFirst = PlayerConfig.IsFirstPlay; #endregion ### Player Config ### _window.ShowUtility(); } private void OnGUI() { ShowEdit(); } private void OnDestroy() { // } /// <summary> /// エディット画面を表示する /// </summary> private void ShowEdit() { _scrollPos = GUILayout.BeginScrollView(_scrollPos, GUI.skin.box); EditorGUILayout.LabelField("---- Player Config ----"); _isFirst = EditorGUILayout.Toggle("初回プレイ: ", _isFirst); GUILayout.EndScrollView(); if (GUILayout.Button("更新")) { Apply(); } } /// <summary> /// PlayerPrefsを更新 /// </summary> private void Apply() { PlayerConfig.IsFirstPlay = _isFirst; } }
これを実際に表示すると以下のようなウィンドウになります。(一部マスク)
ライトマップデータから影の情報を抜き出し頂点カラーに焼く
概要
とあるプロジェクトで頂点カラーにライトマップの影情報を焼き込めないか、という話があって試してみました。
結局その機能自体は使いませんでしたが、ライトマップデータへのアクセスなど学びがあったのでまとめておきます。
ライトマップデータの読み取り
まずはライトマップデータの取り扱いです。
ライトマップは、Lightの「Mode」をMixedかBakedにし、Lightingウィンドウの「Generate Lighting」ボタンを押すことで生成されます。
生成されたライトマップのデータはこんな感じです↓

ライトマップの扱いはLightmapDataクラスを使う
ライトマップのデータは、LightmapDataクラスを介して取得します。
ライトマップデータを取り出す
オブジェクトに紐づくデータは以下のようにして取り出します。
MeshRenderer renderer = GetComponent<MeshRenderer>(); LightmapData data = LightmapSettings.lightmaps[renderer.lightmapIndex]; Texture2D lightmap = data.lightmapColor;
RendererクラスのlightmapIndexプロパティに、該当オブジェクトのライトマップデータの配列のindexが格納されているので、それを利用してLightmapSettings.lightmaps配列からライトマップデータを取得することができます。
ライトマップデータ(テクスチャ)はLightmapData.lightmapColorに格納されています。
ライトマップデータからカラー情報を取得する
ライトマップデータを取り出したら、そこからカラー情報を取得します。
ライトマップは通常、複数オブジェクトの情報がひとつ(ないし複数)のテクスチャに、テクスチャアトラスとして書き出されます。
つまり、ライトマップデータは複数オブジェクトの情報を含んでいるため、適切にテクスチャからカラー情報を取得(フェッチ)しないとなりません。
※ 注意点として、生成されたライトマップデータは読み取りができない状態になっているので、インスペクタの設定から「Read/Write Enabled」のチェックをオンにする必要があります。
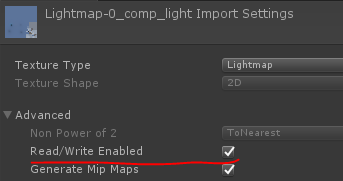
そのための処理は以下のようになります。
int width = lightmap.Width; int height = lightmap.Height; Vector4 scaleOffset = renderer.lightmapScaleOffset; Color[] colors = new Color[mesh.uv.Length]; for (int i = 0; i < mesh.uv.Length; i++) { Vector2 uv = mesh.uv[i]; float uv_x = (uv.x * scaleOffset.x) + scaleOffset.z; float uv_y = (uv.y * scaleOffset.y) + scaleOffset.w; Color pixel = lightmap.GetPixelBilinear(uv_x, uv_y); colors[i] = pixel; } mesh.colors = colors;
上記のように、Renderer.lightmapScaleOffsetに、ライトマップデータのオフセット情報が入っています。
それに、メッシュが持つ元々のUV情報と組み合わせてフェッチすることで、目的のライトマップのカラー情報を取得することができます。
今回はメッシュの頂点カラーに焼き込む、というのが目的なので、最終的に取得したピクセル配列をメッシュの頂点カラーとして設定しています。
そして焼き込んだメッシュ情報を利用する場合、アセットとして新規作成しておかないとならないため、今回のサンプルでは元のメッシュを複製、アセットとして保存する処理もあります。
ということで、今回実装した内容全体を下記に記載しておきます。
Meshを生成する
using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEditor; public static class BakeLightMap2VC { /// <summary> /// Clone mesh asset. /// /// If folder in path doesn't exist, will create all folders in path. /// </summary> public static Mesh CloneMesh(GameObject target) { if (target == null) { Debug.LogWarning("Must select a GameObject."); return null; } MeshFilter filter = target.GetComponent<MeshFilter>(); if (filter == null) { Debug.LogWarning("CloneMesh need a MeshFilter component."); return null; } Mesh newMesh = GameObject.Instantiate(filter.sharedMesh); string[] folderPaths = new[] { "ClonedMesh", }; string path = "Assets"; for (int i = 0; i < folderPaths.Length; i++) { string folderName = folderPaths[i]; string checkPath = path + "/" + folderName; if (!AssetDatabase.IsValidFolder(checkPath)) { AssetDatabase.CreateFolder(path, folderName); } path = checkPath; } // Create and save a mesh asset. string assetPath = path + "/" + target.name + ".asset"; string[] findAssets = AssetDatabase.FindAssets(target.name, new[] { path }); if (findAssets.Length != 0) { int result = EditorUtility.DisplayDialogComplex("重複チェック", "既存のファイルがあります。上書きしますか?", "はい", "いいえ", "別名で保存"); if (result == 1) { return null; } else if (result == 2) { assetPath = AssetDatabase.GenerateUniqueAssetPath(assetPath); } } AssetDatabase.CreateAsset(newMesh, assetPath); AssetDatabase.SaveAssets(); EditorGUIUtility.PingObject(newMesh); return newMesh; } /// <summary> /// Bake a lightmap shadow to vertex colors. /// </summary> [MenuItem("Assets/Tools/BakeLightMap2VC")] public static void Bake() { GameObject target = Selection.activeGameObject; if (target == null) { Debug.LogWarning("Must select a GameObject."); return; } // Clone selected object's mesh. Mesh clonedMesh = CloneMesh(target); if (clonedMesh == null) { Debug.LogError("Can't clone mesh data."); return; } MeshRenderer renderer = target.GetComponent<MeshRenderer>(); if (renderer == null) { Debug.LogWarning("Must have a MeshRenderer."); return; } LightmapData data = LightmapSettings.lightmaps[renderer.lightmapIndex]; Texture2D lightMap = data.lightmapColor; MeshFilter filter = target.GetComponent<MeshFilter>(); filter.sharedMesh = clonedMesh; #region ### Sample LightMap data and bake it to vertex colors ### int width = lightMap.width; int height = lightMap.height; Vector4 scaleOffset = renderer.lightmapScaleOffset; Color[] colors = new Color[clonedMesh.uv.Length]; for (int i = 0; i < clonedMesh.uv.Length; i++) { Vector2 uv = clonedMesh.uv[i]; float uv_x = (uv.x * scaleOffset.x) + scaleOffset.z; float uv_y = (uv.y * scaleOffset.y) + scaleOffset.w; Color pixel = lightMap.GetPixelBilinear(uv_x, uv_y); colors[i] = pixel; } clonedMesh.colors = colors; #endregion ### Sampling LightMap data ### } }
頂点カラーを利用するシェーダ
さて最後に。
頂点カラーに情報を書き込んでも、それを読み出さなくては意味がありません。
そして残念ながら、最近の3Dではあまり頂点カラーを使わないため、Unityのデフォルトのシェーダでは頂点カラー情報は処理されません。
なので、頂点カラーを読み出す処理は自分で書く必要があります。
といっても、頂点カラー情報を取得するにはシェーダへの入力に頂点カラーのパラメータを追加するだけです。
struct v2f
{
fixed4 vertex : SV_POSITION;
fixed4 color : COLOR; // <- これを追加
fixed2 uv : TEXCOORD0;
};
あとはこれを、最終出力に乗算してやるだけでOKです。
half4 frag(v2f i) : SV_Target
{
fixed2 uv = (i.uv * _MainTex_ST.xy) + _MainTex_ST.zw;
fixed4 col = tex2D(_MainTex, uv);
return col * i.color * _Color;
}
シェーダ全体も載せておきます。
Shader "VertexShadow" {
Properties
{
_Color ("Color", Color) = (1,1,1,1)
_MainTex ("Albedo (RGB)", 2D) = "white" {}
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 150
Pass
{
Tags { "LightMode"="ForwardBase" "Queue"="Geometry-10" }
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#pragma target 3.0
#include "UnityCG.cginc"
sampler2D _MainTex;
fixed4 _MainTex_ST;
fixed4 _Color;
struct v2f
{
fixed4 vertex : SV_POSITION;
fixed4 color : COLOR;
fixed2 uv : TEXCOORD0;
};
UNITY_INSTANCING_CBUFFER_START(Props)
UNITY_INSTANCING_CBUFFER_END
v2f vert(appdata_full i)
{
v2f o;
o.vertex = UnityObjectToClipPos(i.vertex);
o.color = i.color;
o.uv = i.texcoord;
return o;
}
half4 frag(v2f i) : SV_Target
{
fixed2 uv = (i.uv * _MainTex_ST.xy) + _MainTex_ST.zw;
fixed4 col = tex2D(_MainTex, uv);
return col * i.color * _Color;
}
ENDCG
}
}
FallBack "Diffuse"
}