Unityでパーリンノイズの実装

概要

今回はパーリンノイズについて書きたいと思います。
以前実装して使ったりしていましたが、しっかりと理論を理解して使ってはいなかったので、改めて、という感じです。

Wikipediaから引用させていただくと、

パーリンノイズ（英: Perlin noise）とは、コンピュータグラフィックスのリアリティを増すために使われるテクスチャ作成技法。擬似乱数的な見た目であるが、同時に細部のスケール感が一定である。このため制御が容易であり、各種スケールのパーリンノイズを数式に入力することで多彩なテクスチャを表現できる。パーリンノイズによるテクスチャは、CGIで自然な外観を物に与えるためによく使われる。

Ken Perlin が Mathematical Applications Group, Inc. で勤務しているときに開発した。彼はこの業績により、1997年、映画芸術科学アカデミーからアカデミー科学技術賞（Technical Achivement）を受賞した。

パーリンノイズは (x,y,z) または (x,y,z,time) の関数として実装され、事前に計算された勾配に従って内挿を行い、時間的/空間的に擬似乱数的に変化する値を生成する。Ken Perlin は2002年に実装を改善し、より自然に見えるようにした（外部リンク参照）。

パーリンノイズは、コンピュータグラフィックスで炎や煙や雲を表現するのによく使われている。また、メモリ使用量が少ないため、メモリ容量が小さい場面でのテクスチャ生成にも使われ、パソコンゲームでのリアルタイムCG生成時にGPU上で使われることが増えている。

実際にレンダリングしてみたのがこれ。Photoshopで「雲模様」ってフィルタ使うと出てくるやつですね。

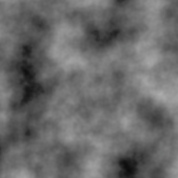
パーリンノイズはいたるところで利用されています。 例えば、以前Unityで実装した「カールノイズ」でも内部的にパーリンノイズを使っていたりします。

edom18.hateblo.jp

---

Table of Contents

---

そして今回改めてこれを書こうと思ったのは、最近ハマっているレイマーチングでフラクタル地形を描きたいな、と思ったのがきっかけです。

ちなみにこちらの記事（非整数ブラウン運動）から引用させていただくと、

周波数を一定の割合で増加させる（lacunarity）と同時に振幅を減らしながら（gain）ノイズを（octaveの数だけ）繰り返し重ねることで、より粒度の細かいディテールを持ったノイズを作り出すことができます。このテクニックは「非整数ブラウン運動（fBM）」または単に「フラクタルノイズ」と呼ばれていて、最も単純な形は下記のコードのようになります。

と書かれています。 これはパーリンノイズの振幅と、周波数をオクターブごとに変えたものを重ね合わせて作るノイズです。 （上のJSでの実装も、まさにこのオクターブを重ね合わせて雲のような模様を作っています）

このフラクタル地形をさらに発展させると以下のようなすばらしい映像を、フラグメントシェーダのみで記述することが可能となります。

https://www.shadertoy.com/view/4sXGRM

目下の目標は上のような海をレンダリングすることです。

なお、今回の記事は以下の記事を大いに参考にさせていただきました。ありがとうございます。

postd.cc

パーリンノイズの考えかた

パーリンノイズは「グラデーションノイズ（勾配ノイズ）」と呼ばれています。
これは後述する、勾配ベクトルを用いたノイズ生成処理に起因しているものと思われます。

パーリンノイズ関数は、0〜1の範囲で値を返す関数です。
ではどのようにしてその値を算出するのでしょうか。

パーリンノイズの値算出

まずは以下の図を見てください。

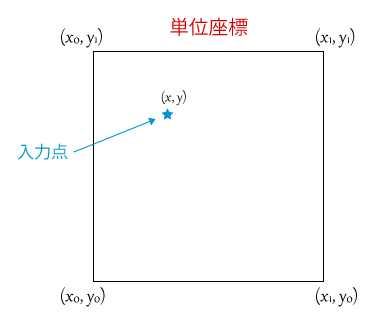
これはパーリンノイズで利用する「単位座標」を図解したものです。
（上記画像は2次元での例ですが、多次元に拡張可能で3次元の場合は図に加えてZの値が入ります）

そして中央やや左上にあるのが入力点の位置です。
つまり、「パーリンノイズ関数への入力」ですね。
（ただし、後述するように0～1でclampされた値となります）

そしてその入力点に対して計算を行い、ノイズとしての最終的な値を算出することになります。

単位座標

なぜ単位座標と呼ぶかと言うと、入力されたx, y, zの値を0〜1の間で繰り返させ、1を超える場合はまた0に戻るように「繰り返し」の状況を作るため「単位」なんですね。

ちなみに擬似コードで示すと以下のイメージです。

[x, y, z] = [x, y, z] % 1.0;

x, y, zの値を1で割った余りを利用することで、0〜1の間で繰り返させるわけです。

疑似乱数勾配ベクトル

単位座標について説明しました。
この単位座標は4つの（3次元なら8つの）勾配ベクトルを持ちます。

この勾配ベクトルは擬似乱数によって生成します。
つまり、勾配ベクトルの方程式に入力された整数に対して、常に同じ結果を返すものです。（なので疑似乱数）

これは、与えられた勾配ベクトル方程式が変わらなければ単位座標が持つ勾配ベクトルは固有の値を持つことを意味します。

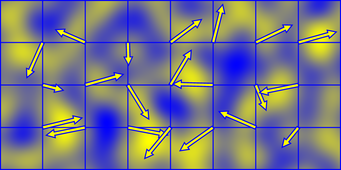
以下の図を見てください。

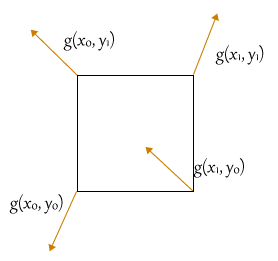
これは、単位座標のそれぞれの頂点に勾配ベクトルを加えた図です。

距離ベクトルを求める

次に、入力点と各頂点からの距離ベクトルを求めます。
距離ベクトルは単純に、入力点から各頂点の位置ベクトルを減算することで求めることができますね。

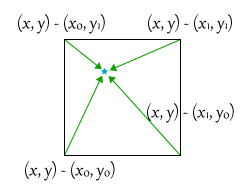
距離ベクトルと勾配ベクトルの内積がノイズに対する影響値

さて、上記で求めた距離ベクトルですが、このベクトルと各頂点の勾配ベクトルとの内積を取ることで入力点に対する各頂点の勾配ベクトルの影響値が算出できます。

なぜ内積を取ると影響値が算出できるのかというと、ベクトルの内積は、言ってしまえばふたつのベクトルが「どれだけ似通っているか」を判断することができるためです。

ちなみに内積の定義は以下のようになります。

そしてもし、ベクトルがまったく同じ方向を向いていたら（つまり平行であったら）、はとなり、結果的にa.length * b.lengthとなります。
（逆に反対を向いていたら反転し-1が乗算されたものと同じ結果になります）

この影響を図示したものを、参考にさせていただいた記事から引用させていただくと以下のようになります。

引用：パーリンノイズを理解する | POSTD

加重平均で最終値を求める

これで、各4頂点との影響値を計算することができました。
最後に、この4頂点の勾配ベクトルを加重平均によって求めます。

まず、各4頂点から得られた勾配ベクトルの影響値を以下のように図示します。

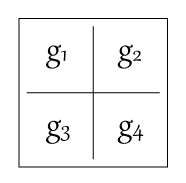
がそれぞれの勾配ベクトルとの内積結果です。
この結果を、それぞれの値の補間を計算し、最終的な値として採用します。

具体的には、疑似コードで表すと以下のようになります。

int g1, g2, g3, g4;
int u, v;

int x1 = lerp(g1, g2, u);
int x2 = lerp(g3, g4, u);

int result = lerp(x1, x2, v);

やっていることは、まず横方向の補間を計算し（および）、その結果をさらに縦方向に補間します。（の補間）

これで補間した結果の値が求まりました。

フェード関数

さて、実はこれではまだ問題があります。
というのも、上記は線形補間をしてしまったために、補間値が折れ線グラフのようになってしまいます。
しかし冒頭に載せた図はそこまでパキっとしていませんね。

そこで、フェード関数と呼ばれる関数を用いて線形補間の係数自体をなめらかに変換することで実現します。

フェード関数は以下の形の関数です。

6t⁵ - 15t⁴ + 10t³

グラフにしてみると以下の図のようになります。

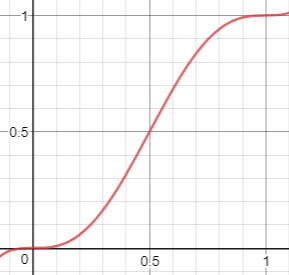
スムーズに変化しているのが分かりますね。

これで、必要な要素が揃いました。

改良版のパーリンノイズ

必要な要素が揃ったと書きましたが、実は改良版のパーリンノイズでは若干異なるアプローチを取っているようです。

ひとつは、勾配ベクトルです。

改良版の勾配ベクトルについてですが、実は正直まだよく理解できていません。

参考にさせていただいた記事から引用すると、

しかしながら、上の図は完全に正確ではありません。この記事で扱っているKen Perlinの改良パーリンノイズでは、これらの勾配は全くの無作為ではありません。立方体の中心点のベクトルから辺に向かって取り出されます。

と書かれています。
上の図というのは本記事でのこの図です↓

図では無作為（ランダム）なように記載されていますが、これが「無作為ではない」というのが引用した文の主張のようです。

そして取り出されるベクトルは以下の12ベクトルになります。

(1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0),
(1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1),
(0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1) 

だいぶ整理されたベクトルの印象を受けますね。
このベクトルについての根拠を、大元の論文（Ken PerlinのSIFFRAPH 2002の論文「Improving Noise」）から引用させてもらうと以下のように記載されています。

The key to removing directional bias in the gradients is to skew the set of gradient directions away from the coordinate axes and long diagonals. In fact, it is not necessary for G to be random at all, since P provides plenty of randomness. The corrected version replaces G with the 12 vectors defined by the directions from the center of a cube to its edges:

ここで言っているのは、ざっくり言うと、勾配ベクトルは、使用しているが十分にランダムなのでランダムである必要はない、ということのようです。

さらに論文ではこう続きます。

Gradients from this set are chosen by using the result of P, modulo 12.

配列の結果から、勾配が選択される、と。
後述する実装例を見てもらうと分かりますが、実際に、計算自体はP配列の結果を元に計算が行われます。

なお、（ここが理解しきれていない点ですが）前段では「距離ベクトルと勾配ベクトルの内積を取る」と説明しました。
しかし、参考にした実装では内積計算を（明示的には）行っていません。

論文をさらに読み進めると以下のように書かれています。

it allows the eight inner products to be effected without requiring any multiplies, thereby removing 24 multiplies from the computation.

乗算を行うことなく、8つの頂点（2次元なら4つ）との内積を得ることができる、と。
このあたりの数学的な理由や原理が理解できていない点です。
しかしながら、「内積を求めてそれを利用する」という「概念」自体は変わっていません。

結局のところ、各頂点と距離ベクトルとの内積を計算しそれを影響値とする、ということ自体は変わらず、その算出方法をより効率的にした、というのが改良版パーリンノイズだと解釈しています。

複数オクターブを利用した表現の拡張

実は今回実装した例では、この「複数オクターブ重ねたノイズ」となっています。
しかしながら、パーリンノイズ自体は前述の説明がすべてです。

これを、さらに「オクターブ」という概念で複数のノイズを生成し、それを合成することでより自然なノイズを生成する、というのが目的です。

ちなみにこの表現を「フラクタルブラウン運動（fractal brownian motion）」と呼ぶようです。
※ おそらく。参考にした記事での実装や、その他の記事を見るに、実装方法はほぼ同じなのでそう解釈しています。

これについては以下の記事を参照ください。

thebookofshaders.com

ちなみに、冒頭でも書いたように、これをさらに発展させた「ドメインワープ」という表現を使って波や動く雲の表現をレイマーチングによって実装するのが目下の目標です。

このドメインワープという方法を実装した例がこちら。（あくまで上の記事で紹介されているコードを、必要な部分だけ抜き出して実装したものです）

fBMをfBMで歪めるドメインワーピング。すごい。 https://t.co/8fJCD1wNe3 参考記事: https://t.co/R3ye88Dc1O pic.twitter.com/vEBvtHUrnX

— edom18@AR / MESON (@edo_m18) 2018年10月10日

最終的にはこれを理解して、実際のコンテンツに盛り込めるようにするのが目標です。
なので今回はこのオクターブでの表現については説明を割愛して、次の記事で詳細に書きたいと思います。

---

[2018.10.18 追記]
Qiitaでドメインワープについての記事を書きました。

qiita.com

---

ソースコード

最後に、C#で実装したソースコードを紹介します。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

/////////////
/// Xorshift。擬似乱数生成用に使用する
public class Xorshift
{
    private uint[] _vec = new uint[4];

    public Xorshift(uint seed = 100)
    {
        for (uint i = 1; i <= _vec.Length; i++)
        {
            seed = 1812433253 * (seed ^ (seed >> 30)) + i;
            _vec[i - 1] = seed;
        }
    }

    public float Random()
    {
        uint t = _vec[0];
        uint w = _vec[3];

        _vec[0] = _vec[1];
        _vec[1] = _vec[2];
        _vec[2] = w;

        t ^= t << 11;
        t ^= t >> 8;
        w ^= w >> 19;
        w ^= t;

        _vec[3] = w;

        return w * 2.3283064365386963e-10f;
    }
}

public class PerlinNoise
{
    private Xorshift _xorshit;
    private int[] _p;
    public float Frequency = 32.0f;

    /// 

    /// Constructor
    /// 
    public PerlinNoise(uint seed)
    {
        _xorshit = new Xorshift(seed);

        int[] p = new int[256];
        for (int i = 0; i < p.Length; i++)
        {
            // 0 - 255の間のランダムな値を生成する
            p[i] = (int)Mathf.Floor(_xorshit.Random() * 256);
        }

        // pの倍の数の配列を生成する
        int[] p2 = new int[p.Length * 2];
        for (int i = 0; i < p2.Length; i++)
        {
            p2[i] = p[i & 255];
        }

        _p = p2;
    }

    private float Fade(float t)
    {
        // 6t^5 - 15t^4 + 10t^3
        return t * t * t * (t * (t * 6f - 15f) + 10f);
    }

    /// 

    /// Linear interpoloation
    /// 
    private float Lerp(float t, float a, float b)
    {
        return a + t * (b - a);
    }

    /// 

    /// Calculate gradient vector.
    /// 
    private float Grad(int hash, float x, float y, float z)
    {
        // 15 == 0b1111 : Take the first 4 bits of it.
        int h = hash & 15;
        float u = (h < 8) ? x : y;
        float v = (h < 4) ? y : (h == 12 || h == 14) ? x : z;
        return ((h & 1) == 0 ? u : -u) + ((h & 2) == 0 ? v : -v);
    }

    /// 

    /// To simplify above function to below.
    /// 
    // private float Grad(int hash, float x, float y, float z)
    // {
    //     switch(hash & 0xF)
    //     {
    //         case 0x0: return  x + y;
    //         case 0x1: return -x + y;
    //         case 0x2: return  x - y;
    //         case 0x3: return -x - y;
    //         case 0x4: return  x + z;
    //         case 0x5: return -x + z;
    //         case 0x6: return  x - z;
    //         case 0x7: return -x - z;
    //         case 0x8: return  y + z;
    //         case 0x9: return -y + z;
    //         case 0xA: return  y - z;
    //         case 0xB: return -y - z;
    //         case 0xC: return  y + x;
    //         case 0xD: return -y + z;
    //         case 0xE: return  y - x;
    //         case 0xF: return -y - z;
    //         default: return 0; // never happens
    //     }
    // }

    private float Noise(float x, float y = 0, float z = 0)
    {
        // Repeat while 0 - 255
        int X = (int)Mathf.Floor(x) & 255;
        int Y = (int)Mathf.Floor(y) & 255;
        int Z = (int)Mathf.Floor(z) & 255;

        // trim integer
        x -= Mathf.Floor(x);
        y -= Mathf.Floor(y);
        z -= Mathf.Floor(z);

        float u = Fade(x);
        float v = Fade(y);
        float w = Fade(z);

        int[] p = _p;

        #region ### calulate hashes from array of p ###
        int A, B, AA, AB, BA, BB, AAA, ABA, AAB, ABB, BAA, BBA, BAB, BBB;

        A = p[X + 0] + Y; AA = p[A] + Z; AB = p[A + 1] + Z;
        B = p[X + 1] + Y; BA = p[B] + Z; BB = p[B + 1] + Z;

        AAA = p[AA + 0]; ABA = p[BA + 0]; AAB = p[AB + 0]; ABB = p[BB + 0];
        BAA = p[AA + 1]; BBA = p[BA + 1]; BAB = p[AB + 1]; BBB = p[BB + 1];
        #endregion ### calulate hashes from array of p ###

        float a = Grad(AAA, x + 0, y + 0, z + 0);
        float b = Grad(ABA, x - 1, y + 0, z + 0);
        float c = Grad(AAB, x + 0, y - 1, z + 0);
        float d = Grad(ABB, x - 1, y - 1, z + 0);
        float e = Grad(BAA, x + 0, y + 0, z - 1);
        float f = Grad(BBA, x - 1, y + 0, z - 1);
        float g = Grad(BAB, x + 0, y - 1, z - 1);
        float h = Grad(BBB, x - 1, y - 1, z - 1);

        return Lerp(w, Lerp(v, Lerp(u, a, b),
                               Lerp(u, c, d)),
                       Lerp(v, Lerp(u, e, f),
                               Lerp(u, g, h)));
    }

    public float OctaveNoise(float x, int octaves, float persistence = 0.5f)
    {
        float result = 0;
        float amp = 1.0f;
        float f = Frequency;
        float maxValue = 0;

        for (int i = 0; i < octaves; i++)
        {
            result += Noise(x * f) * amp;
            f *= 2.0f;
            maxValue += amp;
            amp *= persistence;
        }

        return result / maxValue;
    }

    public float OctaveNoise(float x, float y, int octaves, float persistence = 0.5f)
    {
        float result = 0;
        float amp = 1.0f;
        float f = Frequency;
        float maxValue = 0;

        for (int i = 0; i < octaves; i++)
        {
            result += Noise(x * f, y * f) * amp;
            f *= 2.0f;
            maxValue += amp;
            amp *= persistence;
        }

        return result / maxValue;
    }

    public float OctaveNoise(float x, float y, float z, int octaves, float persistence = 0.5f)
    {
        float result = 0;
        float amp = 1.0f;
        float f = Frequency;
        float maxValue = 0;

        for (int i = 0; i < octaves; i++)
        {
            result += Noise(x * f, y * f, z * f) * amp;
            f *= 2.0f;
            maxValue += amp;
            amp *= persistence;
        }

        return result / maxValue;
    }
}

これを実際に利用するコードは以下のようになります。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class PerlinNoiseTest : MonoBehaviour
{
    [SerializeField]
    private GameObject _quad;

    [SerializeField]
    [Range(1, 16)]
    private int _octaves = 5;

    [SerializeField]
    [Range(0.1f, 64.0f)]
    private float _frequency = 32.0f;

    [SerializeField]
    private float _persistence = 0.5f;

    [SerializeField]
    private int _width = 512;

    [SerializeField]
    private int _height = 512;

    [SerializeField]
    private uint _seed = 1000;

    private PerlinNoise _noise;
    private PerlinNoise Noise
    {
        get
        {
            if (_noise == null)
            {
                _noise = new PerlinNoise(_seed);
            }
            return _noise;
        }
    }
    private Texture2D _texture;

    private void Start()
    {
        CreateNoise();
    }

    private void OnValidate()
    {
        if (Application.isPlaying)
        {
            CreateNoise();
        }
    }

    private void CreateNoise()
    {
        _texture = new Texture2D(_width, _height, TextureFormat.RGBA32, false);

        Noise.Frequency = _frequency;

        Color[] pixels = new Color[_width * _height];
        float fx = 1f / (float)_width;
        float fy = 1f / (float)_height;
        for (int i = 0; i < pixels.Length; i++)
        {
            int x = i % _width;
            int y = i / _width;
            float n = Noise.OctaveNoise(x * fx, y * fy, _octaves, _persistence);
            float c = Mathf.Clamp(218f * (0.5f + n * 0.5f), 0f, 255f) / 255f;
            pixels[i] = new Color(c, c, c, 1f);
        }

        _texture.SetPixels(0, 0, _width, _height, pixels);
        _texture.Apply();

        Renderer renderer = _quad.GetComponent();
        renderer.material.mainTexture = _texture;
    }
}

これを、シーンに配置したQuadに設定して実行すると以下のような結果になります。

なお、今回のパーリンノイズの実装はGithubにアップしてあります。

github.com

シンプル版パーリンノイズ

のたぐすさんの以下の記事で書かれているコードをベースに、最近では簡易版として以下のファイルを作って利用しています。

wordpress.notargs.com

シンプル版パーリンノイズとカールノイズ

ちなみにカールノイズもよく使うので一緒に入れています。が、やはり負荷が高めなのであまり多様はできません。

#ifndef __NOISEMATH_CGINC__
#define __NOISEMATH_CGINC__

float rand(float x)
{
    return frac(sin(x) * 43758.5453);
}

float rand(float2 co)
{
    return frac(sin(dot(co.xy, float2(12.9898, 78.233))) * 43758.5453);
}

float rand(float3 co)
{
    return frac(sin(dot(co.xyz, float3(12.9898, 78.233, 56.787))) * 43758.5453);
}

float2x2 rot(float a)
{
    float s = sin(a);
    float c = cos(a);
    return float2x2(c, -s, s, c);
}

float noise(float3 pos)
{
    float3 ip = floor(pos);
    float3 fp = smoothstep(0, 1, frac(pos));
    float4 a = float4(
        rand(ip + float3(0, 0, 0)),
        rand(ip + float3(1, 0, 0)),
        rand(ip + float3(0, 1, 0)),
        rand(ip + float3(1, 1, 0)));
    float4 b = float4(
        rand(ip + float3(0, 0, 1)),
        rand(ip + float3(1, 0, 1)),
        rand(ip + float3(0, 1, 1)),
        rand(ip + float3(1, 1, 1)));

    a = lerp(a, b, fp.z);
    a.xy = lerp(a.xy, a.zw, fp.y);
    return lerp(a.x, a.y, fp.x);
}

float perlin(float3 pos)
{
    return
        (noise(pos) * 32 +
         noise(pos * 2) * 16 +
         noise(pos * 4) * 8 +
         noise(pos * 8) * 4 +
         noise(pos * 16) * 2 +
         noise(pos * 32)) / 63;
}

/// パーリンノイズによるベクトル場
/// 3Dとして3要素を計算。
/// それぞれのノイズは明らかに違う（極端に大きなオフセット）を持たせた値とする
float3 Pnoise(float3 vec)
{
    float x = perlin(vec);

    float y = perlin(float3(
        vec.y + 31.416,
        vec.z - 47.853,
        vec.x + 12.793
    ));

    float z = perlin(float3(
        vec.z - 233.145,
        vec.x - 113.408,
        vec.y - 185.31
    ));

    return float3(x, y, z);
}

float3 CurlNoise(float3 pos)
{
    const float e = 1e-4f;
    const float e2 = 2.0 * e;
    const float invE2 = 1.0 / e2;

    const float3 dx = float3(e, 0.0, 0.0);
    const float3 dy = float3(0.0, e, 0.0);
    const float3 dz = float3(0.0, 0.0, e);

    float3 p_x0 = Pnoise(pos - dx);
    float3 p_x1 = Pnoise(pos + dx);
    float3 p_y0 = Pnoise(pos - dy);
    float3 p_y1 = Pnoise(pos + dy);
    float3 p_z0 = Pnoise(pos - dz);
    float3 p_z1 = Pnoise(pos + dz);

    float x = (p_y1.z - p_y0.z) - (p_z1.y - p_z0.y);
    float y = (p_z1.x - p_z0.x) - (p_x1.z - p_x0.z);
    float z = (p_x1.y - p_x0.y) - (p_y1.x - p_y0.x);

    return float3(x, y, z) * invE2;
}

#endif