Unityでガウシアンブラーを実装する
概要
よく使う&表現力の高いぼかし処理。
以前にもぼかしを利用したコンテンツを作成したり、記事を書いたりしていましたがちゃんとぼかしだけにフォーカスしたことはなかったので改めて書きたいと思います。
今回のサンプルを動かしたデモ↓

ちなみに以前、ぼかし関連の内容が含まれていたコンテンツ/記事はこんな感じ↓
なお、今回の記事はこちらの記事を参考にさせていただきました。
あとこちらも。
また、今回のサンプルは以下にアップしてあります。
ガウス関数とは
Wikipediaから引用させてもらうと以下のように説明されています。
ガウス関数(ガウスかんすう、英: Gaussian function)は、
の形の初等関数である。なお、 のかわりに
とするなど、表し方にはいくつかの変種がある。
ガウシアン関数、あるいは単にガウシアンとも呼ばれる。
また、特徴として以下のようにも説明されています。
特徴
は、ガウス関数の1種である。
ということで、今回話題にするのはこちらの関数です。
ここでの大事な点としては「正規分布関数」ということでしょう。
これもWikipediaから引用させてもらうと、
平均値の付近に集積するようなデータの分布を表した連続的な変数に関する確率分布
と書かれています。
ガウス関数では上記関数のの値を
0にすると、を中心とした釣り鐘型のグラフを描きます。
これが、ぼかしを掛ける重み付けとして重宝する点です。
そしてさらに、の値を調整することでグラフの形を調整することができるため、ぼかし具合もパラメータのみで設定できるのが利用される理由でしょう。
ちなみにこの関数をdesmosでグラフ化すると以下のようになります。
上記グラフはの値を変化させた結果です。
尖っていたり、平になっていたり、と形が大きく変化しているのが分かるかと思います。
そして今回利用する関数は、定数部分を1にし、中央がx = 0となるよう、の値を
0とした以下の関数を用います。
これをグラフにすると以下の形になります。
すべてのグラフが1を最大値として色々な形に変化しているのが分かるかと思います。
このグラフのの値を重みとし、さらに
の値をサンプリング点からの距離として用いることでブラーを実現します。
ブラーの仕組み
さて、ガウス関数を使ってブラーさせることが分かりましたが、これをどう利用するのか。
まずは以下の画像を見てください。
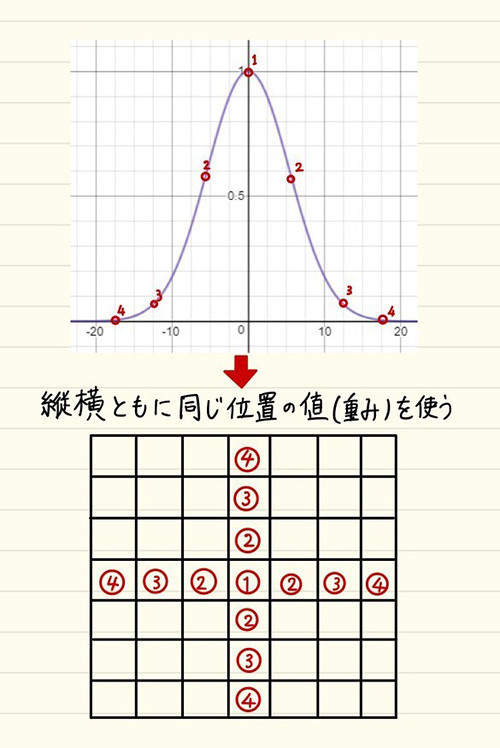
重みの計算
上がガウス関数のグラフの様子、下がテクスチャからテクセルをサンプリングする様子です。
(1)の部分が普通にフェッチするテクスチャの位置を表しています。
そこから(2), (3), (4)が追加でサンプリングするオフセット位置です。
そしてその数字とグラフ上に書かれた数字がそれぞれ、重みとして紐付いた状態を表しています。
つまり、(1)の場合は重み1、(2)の場合はおよそ0.58、という具合です。
中心から離れるにつれて徐々に重みが減っていっているのが分かるかと思います。
ガウス関数を思い出してみるととなっているので、大まかには
expの値に近いカーブを描くことなるわけです。
(そして引数がを用いているためマイナスが取れて左右対称になっている、というわけですね)
ただし、重みは通常「合計して1になる」必要があるので、最終的な重みは全重みの合計でそれぞれの値を割った値として正規化して利用します。
上下左右は別々に計算できる
概ねブラーの処理についてはイメージできたと思います。
ガウシアンブラーを利用するもうひとつの利点として以下のような性質があります。
wgld.orgの記事から引用させていただくと以下のように記載されています。
さらに、ガウス関数を三次元で用いる場合には x 方向と y 方向を切り離して処理することができます。実はこれが非常に重要です。
どういうことかと言うと、仮に上記のように「切り離して処理することができない」とすると、1テクセルの計算に対しては上の図で言うと、数字の書かれていないテクセルに関してもフェッチして処理しないとなりません。
つまり7 x 7 = 49回のフェッチが必要となります。
しかしこれを分離して考えることができる、という性質から「横方向に7回」、「縦方向に7回」というふうに分けて処理することができることを意味します。
結果、7 x 7 = 49だったフェッチ回数が7 + 7 = 14という回数に劇的に少なくなるわけです。
(そしてこれは、対象とするテクセル数が増えれば増えるほど顕著に差が出てきます)
実際にブラーがかかっていく様子を、Frame Debuggerで出力された画像を見てみると以下のように3回のパスを経て生成されています。
まず、テクスチャをコピーします。(またブラーの性質上、対象画像が縮小されてもあまり問題ないため半分のスケールにしてからコピーしています)

そしてまず、横方向にブラーをかけます↓

さらに横方向ブラーがかかった画像に対して縦にブラーをかけます↓

最終的にしっかりとブラーがかかっているのが分かるかと思います。
シェーダを実装する
仕組みが分かったところでシェーダの実装です。
あまり長いコードではないので全文載せます。
Shader "Custom/BlurEffect"
{
Properties
{
_MainTex("Texture", 2D) = "white" {}
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 100
Pass
{
ZTest Off
ZWrite Off
Cull Back
CGPROGRAM
#pragma fragmentoption ARB_precision_hint_fastest
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float4 vertex : SV_POSITION;
half2 uv : TEXCOORD0;
};
sampler2D _MainTex;
half4 _Offsets;
static const int samplingCount = 10;
half _Weights[samplingCount];
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
return o;
}
fixed4 frag (v2f i) : SV_Target
{
half4 col = 0;
[unroll]
for (int j = samplingCount - 1; j > 0; j--)
{
col += tex2D(_MainTex, i.uv - (_Offsets.xy * j)) * _Weights[j];
}
[unroll]
for (int j = 0; j < samplingCount; j++)
{
col += tex2D(_MainTex, i.uv + (_Offsets.xy * j)) * _Weights[j];
}
return col;
}
ENDCG
}
}
}
一番重要なのはフラグメントシェーダでしょう。
samplingCount分だけfor文でループしているのが分かるかと思います。
ふたつループがあるのは、中心から左右(あるいは上下)にテクセルをフェッチするためそれぞれ2回に分けて書いているだけです。
必要となるオフセット位置についてはC#側から設定して計算しています。
また同様に、重みに関してもC#側から渡しています。
理由としては、パラメータが変化しなければ重みに変化がないためアップデートが必要なときだけ計算を行っているためです。
次に、C#の実装を見てみます。
using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEngine.Rendering; namespace Sample { public class GaussianBlur : MonoBehaviour { [SerializeField] private Texture _texture; [SerializeField] private Shader _shader; [SerializeField, Range(1f, 10f)] private float _offset = 1f; [SerializeField, Range(10f, 1000f)] private float _blur = 100f; private Material _material; private Renderer _renderer; // Apply sevral blur effect so use as double buffers. private RenderTexture _rt1; private RenderTexture _rt2; private float[] _weights = new float[10]; private bool _isInitialized = false; #region ### MonoBehaviour ### private void Awake() { Initialize(); } private void OnValidate() { if (!Application.isPlaying) { return; } UpdateWeights(); Blur(); } #endregion ### MonoBehaviour ### /// <summary> /// Initialize (setup) /// </summary> private void Initialize() { if (_isInitialized) { return; } _material = new Material(_shader); _material.hideFlags = HideFlags.HideAndDontSave; // Down scale. _rt1 = new RenderTexture(_texture.width / 2, _texture.height / 2, 0, RenderTextureFormat.ARGB32); _rt2 = new RenderTexture(_texture.width / 2, _texture.height / 2, 0, RenderTextureFormat.ARGB32); _renderer = GetComponent<Renderer>(); UpdateWeights(); _isInitialized = true; } /// <summary> /// Do blur to the texture. /// </summary> public void Blur() { if (!_isInitialized) { Initialize(); } Graphics.Blit(_texture, _rt1); _material.SetFloatArray("_Weights", _weights); float x = _offset / _rt1.width; float y = _offset / _rt1.height; // for horizontal blur. _material.SetVector("_Offsets", new Vector4(x, 0, 0, 0)); Graphics.Blit(_rt1, _rt2, _material); // for vertical blur. _material.SetVector("_Offsets", new Vector4(0, y, 0, 0)); Graphics.Blit(_rt2, _rt1, _material); _renderer.material.mainTexture = _rt1; } /// <summary> /// Update waiths by gaussian function. /// </summary> private void UpdateWeights() { float total = 0; float d = _blur * _blur * 0.001f; for (int i = 0; i < _weights.Length; i++) { // Offset position per x. float x = i * 2f; float w = Mathf.Exp(-0.5f * (x * x) / d); _weights[i] = w; if (i > 0) { w *= 2.0f; } total += w; } for (int i = 0; i < _weights.Length; i++) { _weights[i] /= total; } } } }
C#のコードのほうがやや長いですね。
ただ、フィールドの定義以外はそこまで処理は多くありません。
まず、今回の主題である「ガウス関数」での重み付けを更新しているのがUpdateWeightsメソッドです。
private void UpdateWeights() { float total = 0; float d = _blur * _blur * 0.001f; for (int i = 0; i < _weights.Length; i++) { // Offset position per x. float x = i * 2f; float w = Mathf.Exp(-0.5f * (x * x) / d); _weights[i] = w; if (i > 0) { w *= 2.0f; } total += w; } for (int i = 0; i < _weights.Length; i++) { _weights[i] /= total; } }
_blurはブラーの強さの係数です。
続くループ処理では各テクセルの重みを計算しています。
xは中心からどれくらい離れているか、を示す値です。まさに関数のxと同義ですね。
ただ、2倍にしているのは入力であるxの値を若干オフセットさせています。(オフセットは値が大きめにばらけるようにしているだけなので、なくても大丈夫です)
そして最後に、求めたそれぞれの重みを、重み全体の合計で割ることで正規化しています。
ブラーのためのダブルバッファ
次に、バッファの準備です。
上で書いたように、縦横それぞれのブラーを適用するためふたつのバッファを用意して処理を行います。
そのため、以下のようにふたつのRenderTexutreを用意します。(と同時に、対象となるテクスチャの半分のサイズにしてダウンスケールしています)
また、ブラーに利用するマテリアルを生成しておきます。
_material = new Material(_shader); _material.hideFlags = HideFlags.HideAndDontSave; // Down scale. _rt1 = new RenderTexture(_texture.width / 2, _texture.height / 2, 0, RenderTextureFormat.ARGB32); _rt2 = new RenderTexture(_texture.width / 2, _texture.height / 2, 0, RenderTextureFormat.ARGB32);
そして実際にブラー処理を行っているのが以下の箇所です。
public void Blur() { Graphics.Blit(_texture, _rt1); _material.SetFloatArray("_Weights", _weights); float x = _offset / _rt1.width; float y = _offset / _rt1.height; // for horizontal blur. _material.SetVector("_Offsets", new Vector4(x, 0, 0, 0)); Graphics.Blit(_rt1, _rt2, _material); // for vertical blur. _material.SetVector("_Offsets", new Vector4(0, y, 0, 0)); Graphics.Blit(_rt2, _rt1, _material); _renderer.material.mainTexture = _rt1; }
冒頭でテクスチャのコピーを行い、必要な重みを設定しています。
その後、必要なテクセルフェッチ位置のオフセットを計算し設定しています。
ちなみにここでのオフセットは、シェーダを見てもらうと分かりますが、フェッチするテクセルごとのオフセットです。
つまり、仮にここで2(相当。実際はUV値なので少数になる)を渡したとすると、通常のフェッチ位置を0として、2, 4, 6, 8...と、2テクセル隣のテクセルを、サンプリング回数分飛び飛びにフェッチしていくことになるわけです。
なのでオフセットの値を大きくするとボケをより大きくすることができます。
(ただし、飛び飛びでの処理になるので大きすぎるとブラーというより「ズレ」のような効果になります)
今回実装したブラー処理は以上です。
なお、この処理をCommand Bufferなどを用いて適切なタイミングでキャプチャした映像を用いると以下のような、擦りガラス的な表現を行うこともできます。

これは公式のサンプルで掲載されているものですが、こちらのサンプルではもう少しシンプルなブラー処理になっています。
あるいは場面転換とかで全体にブラーを適用してもいいかもしれませんね。
ECSでComponentSystemを自作する
カヤックと自分との関わり
この記事はex-KAYAC Advent Calendar 2018の22日目の記事です。
ということで、少しだけカヤックについての話を。
自分はカヤックへはWebのフロントエンドエンジニアとして入社。
その後は4年ほどWebのフロントエンドエンジニアとして働き、当時は「HTMLファイ部」という部署のリーダーをしていまいた。
そしてある日突然、「iOSやってくんない?」というオーダーを受け、Lobiというゲーム向けのSNSサービスのiOS版アプリの開発に携わることに。
それまでiOSを触ったことがなかったので1ヶ月間、ひたすらiOSのドキュメントや記事を読み漁り、それをひたすらQiitaにまとめる毎日でした。
なので自分の記事リストを見るとiOS/Objective-C要素がだいぶ多めになっていますw
さらにその後、Oculus Rift DK1が登場しカヤック内でそれを持っている人がいたため体験することに。このときにVRに一気に惚れ込み、個人的にVR制作を始めました。
そしていよいよVRメインでやりたいと思った折に、コロプラにいた友人からVRエンジニアの募集を強化していることを聞いて今に至る、という感じです。
概要
ということで本題へ。
前回書いたECS入門の続編です。
前の記事ではECSを利用して画面にオブジェクトを描画するまでを書きました。
今回はもう少し踏み込んで、自分でカスタムのシステムを作って利用する流れを書きたいと思います。
このあたりがしっかりと身につけば、あとは応用で色々なシステムが作れるようになると思います。
今回の記事を書くにあたっては、のたぐすさんの以下の記事を参考にさせていただきました。
なお、今回の記事で書いているコードは前回の記事にも掲載したGithubに追記という形で公開しています。
大まかな考え方
まず必要な考え方は「データ指向設計」です。
データ指向については前回の記事で少しだけ書いたので詳細はそちらをご覧ください。
前回書いた部分を抜粋すると、
なぜデータに着目?
オブジェクト指向は人間がイメージしやすい形でプログラムを書いていくことができるので理解しやすい部類でしょう。(色々解釈などによる議論とかは見ますが)
しかし、コンピュータは「オブジェクト」という概念で物を見るのではなく、あくまでバイナリ表現されたデータを、それがなにかを考えずに黙々と処理していきます。
つまり、オブジェクトごとにまとめられたデータというのは、コンピュータからはまったく関係ない・・・どころか、作業効率の邪魔になり得ます。
実際の例で考えてみると、例えばこう考えてみてください。 あなたは自動販売機に飲み物を補充している店員だとします。
そして補充用の箱には「キリン」とか「サントリー」とか「明治」とかメーカーごとに商品が分けられて入れられています。
しかし、補充する側としては「今補充したい飲み物」だけを詰めてくれた箱があったほうが効率がいいですよね。 例えばコーヒーを補充しているのに、水やら別のものが箱に入っているとより分けて補充しなければなりません。
データ指向はまさにこの「補充したい飲み物だけ」を提供する形にデータを整形して処理するもの、と考えることができます。 こうすることによってCPUが効率よく処理することができるようになるというわけなんですね。
大雑把に言えば、CPUが効率よく処理するためにデータの構造を最適化する設計、という感じです。
そのためComponentSystemを理解する上で、この「データ指向」の考え方は重要となります。
「ComponentSystem」は2つある
ECSを利用するにあたって「ComponentSystem」がデータの処理を行います。
前回の記事では描画周りについて既存のシステムを利用してレンダリングしていました。
そして当然ですが、この「システム」は自作することができます。
必要な手順に沿ってクラスを実装することで自作したデータを利用した処理系を作ることができます。
ComponentSystemとJobComponentSystem
ふたつあるシステムとは「ComponentSystem」と「JobComponentSystem」のふたつです。
役割としてはどちらも同様ですが、JobComponentSystemはUnityが実装を進めている「JobSystem」を利用するところが異なります。
JobSystemについても後日記事を書きたいと思っていますが、ものすごくざっくりと言うと「Unityの持っているスレッドの空き時間に、ユーザのスクリプト実行を差し込める」というものです。
要は、Unityの処理の中で余らせている時間を有効に使おう、という趣旨の仕組みです。
JobSystemについてはテラシュールブログさんの以下の記事が詳しく書かれています。
ComponentSystemを自作する勘所
さて、ふたつあるComponentSystemですが、作る際の勘所というか、どう理解していったらいいかは「データの構造の定義と利用」というイメージです。
以下から、実際のコードを例にしながら解説していきます。
データの構造を決める
冒頭で書いたように、ECSは「データ指向設計」になっているので、なにはなくとも「データの構造」を定義するところから始めます。
そして「定義した構造別にシステムを作っていく」イメージです。
データの構造のサンプルを見てみましょう。(データの構造自体はのたぐすさんの記事を参考にしたものになっています)
using System.Collections; using System.Collections.Generic; using UnityEngine; using Unity.Entities; using Unity.Mathematics; // 速度を表すデータ public struct Velocity : IComponentData { public float3 Value; public Velocity(float3 value) { Value = value; } }
なんのことはない、速度データを表す構造体です。
IComponentDataを実装した構造体を作るとComponentSystemで利用することができるようになります。
速度なので、位置の更新が必要となります。
ということで、システムが要求するデータの構造定義を以下のように行います。
Entityとデータ構造を結びつける
システムの要求する構造の前に、Entityと構造の定義を先に解説します。
Entityとシステムを結びつけるのは「データの構造」です。
そのためにはEntityがどんなデータ構造を持っているかの定義が必要です。
定義は以下のように行います。
// ワールドに所属する「EntityManager」を作成する EntityManager manager = World.Active.CreateManager<EntityManager>(); // ... 中略 ... // 「データの構造(Archetype = データアーキテクチャ)」を定義する EntityArchetype archetype = manager.CreateArchetype( typeof(Velocity), typeof(Position), typeof(MeshInstanceRenderer) );
CreateArchetypeメソッドによってデータ構造(データアーキテクチャ)を定義しています。
Entityの生成にはこのEntityArchetypeオブジェクトを引数に取るため、そこで構造とEntityが結び付けられます。
生成は以下のようになります。
Entity entity = manager.CreateEntity(archetype);
これで、定義したデータ構造を持ったEntityがひとつ、ワールドに生成されました。
システムが要求する「グループ」を定義する
次にEntityとシステムを結びつける定義を行います。
なお、この結びつけはComponentSystemとJobComponentSystemで若干異なります。
が、基本的には「データ構造を結びつける」という考え方はどちらも同じです。
まずはComponentSystemのほうから見てみましょう。
using System.Collections; using System.Collections.Generic; using UnityEngine; using Unity.Entities; using Unity.Transforms; using Unity.Rendering; using Unity.Collections; // ComponentSystemが要求するデータ構造を定義する public struct VelocityGroup { // ここでは「Position」と「Velocity」の2つのデータを要求することを定義している public ComponentDataArray<Position> Position; public ComponentDataArray<Velocity> Velocity; // 速度更新のシステムでは利用しないが、 // SharedComponentを要求する場合は`ReadOnly`属性をつける必要がある // 例) // [ReadOnly] // public SharedComponentDataArray<MeshInstanceRenderer> Renderer; // Entityの数を示すLengthフィールドを定義 public readonly int Length; }
まず、冒頭でVelocityGroupという構造体を定義しています。
その定義の内容はシステムが利用するために必要なComponentDataArrayです。
具体的にはPositionとVelocityを要求する形になっています。
そして最後に、該当するデータ構造を持ったEntityの数を示すLengthフィールドを定義しています。
ただ、インターフェースもなにも実装していないしなにを持ってシステムと結びつけるのかと疑問に持たれる人もいるかもしれません。
紐づけに関しては、システムの定義側でInjectすることで解決しています。
システムとグループは「Inject」によって紐付ける
システムのコードを見てみましょう。
// ... VelocityGroupの定義 public class VelocitySystem : ComponentSystem { [Inject] private VelocityGroup _velocityGroup; protected override void OnUpdate() { float deltaTime = Time.deltaTime; for (int i = 0; i < _velocityGroup.Length; i++) { Position pos = _velocityGroup.Position[i]; pos.Value += _velocityGroup.Velocity[i].Value * deltaTime; _velocityGroup.Position[i] = pos; } } }
意外にシンプルですね。
まずComponentSystemを継承し、必要なメソッドをオーバーライドします。
上で定義したグループとの紐づけですが、[Inject]アトリビュートを使って注入しています。
こうすることでシステムが要求するデータ構造が決まり、該当するEntityがワールドに存在している場合にシステムが起動され、処理が実行される、という仕組みになっています。
ComponentTypes
ここは余談になりますが、ComponentTypesというものが存在します。
これはなにかというと、Entityのデータ構造を認識するためのものです。
このあたりについては以下の記事がとても詳細にまとめてくれているので、興味がある方は見てみるといいでしょう。
そこから引用させてもらうと以下のように記載されています。
ComponentGroupはComponentTypes(ComponentDataの型に応じたint型の識別用タグ)の配列を持ち、初期化後変更されることはないです。
つまり、ComponentGroupというフィルターの役割をするものがあり、そこで利用されるのがComponentTypesということです。
そして初期化時にComponentDataを識別するタグの配列を持ち、以降変更されることがありません。
この情報を元に、該当するデータを持つEntityを決定している、というわけなんですね。
ワールドを生成し、システムを登録する
最後はWorldを生成し、その中で必要なシステムを登録します。
こちらもコードを先に見てみましょう。
using System.Collections; using System.Collections.Generic; using UnityEngine; using Unity.Entities; using Unity.Rendering; using Unity.Transforms; using Unity.Mathematics; public class VelocityWorld : MonoBehaviour { [SerializeField] private Mesh _mesh; [SerializeField] private Material _material; [SerializeField] private bool _useJobSystem = false; private void Start() { World.DisposeAllWorlds(); World.Active = new World("VelocityWorld"); EntityManager manager = World.Active.CreateManager<EntityManager>(); World.Active.CreateManager<EndFrameTransformSystem>(); World.Active.CreateManager<RenderingSystemBootstrap>(); if (_useJobSystem) { World.Active.CreateManager<VelocityJobSystem>(); } else { World.Active.CreateManager<VelocitySystem>(); } EntityArchetype archetype = manager.CreateArchetype( typeof(Velocity), typeof(Position), typeof(MeshInstanceRenderer) ); Entity entity = manager.CreateEntity(archetype); manager.SetSharedComponentData(entity, new MeshInstanceRenderer { mesh = _mesh, material = _material, }); manager.SetComponentData(entity, new Velocity { Value = new float3(0, 1f, 0) }); manager.SetComponentData(entity, new Position { Value = new float3(0, 0, 0) }); manager.Instantiate(entity); ScriptBehaviourUpdateOrder.UpdatePlayerLoop(World.Active); } }
JobComponentSystem版も含まれているので分岐が入っていますが、そのシステムの登録部分以外はまったく同じなのが分かるかと思います。
冒頭でワールドの作成と、必要なシステムの登録を行っています。
そして最後の部分でEntityのデータ構造を定義し、その定義を元にEntityを生成しているわけです。
これを実行すると以下のように、少しずつ上に上昇するCubeが表示されます。

速度を上方向に設定しているのでそちらの方向に動いているわけですね。
JobComponentSystemの作成
さて、一歩戻ってJobComponentSystem版を見てみましょう。
using System.Collections; using System.Collections.Generic; using UnityEngine; using Unity.Entities; using Unity.Jobs; using Unity.Burst; using Unity.Transforms; public class VelocityJobSystem : JobComponentSystem { [BurstCompile] struct Job : IJobProcessComponentData<Velocity, Position> { readonly float _deltaTime; public Job(float deltaTime) { _deltaTime = deltaTime; } public void Execute(ref Velocity velocity, ref Position position) { position.Value += velocity.Value * _deltaTime; } } protected override JobHandle OnUpdate(JobHandle inputDeps) { Job job = new Job(Time.deltaTime); return job.Schedule(this, inputDeps); } }
こちらもシンプルですね。
ComponentSystem版との違いを見ていきましょう。
IJobProcessComponentDataを定義に用いる
ComponentSystemではGroupの構造体を定義し、それを[Inject]アトリビュートによって構造とシステムとの紐づけを行っていました。
しかし、JobComponentSystemではIJobProcessComponentDataを利用して紐づけを行います。
IJobProcessComponentDataはインターフェースになっていて、これを実装したJobという単位を作成します。
JobSystemを利用するわけなので、Jobで処理をする形になります。
また注意点として、Jobは別スレッドで実行されるためTime.deltaTimeが利用できません。
そのため、Jobのコンストラクタで値を設定し、それを利用して位置の更新を行っています。
あとは、MeshInstanceRendererSystemなどのシステムがPositionデータなどを用いてレンダリングを行ってくれるためそれ以外の処理は必要ありません。
ECSは比較的データを少なくし、処理単位もミニマムにしていくのが適しているのでひとつひとつのシステムはとてもシンプルになりますね。
IJobProcessComponentDataの拡張メソッド
さて、唐突にJob構造体のScheduleというメソッドを実行していますが、これは拡張メソッドとして定義されいます。
そのため、IJobProcessComponentDataインターフェースを実装すると自動的に拡張されるようになっています。
定義を見てみると以下のように、いくつかの拡張メソッドが定義されているのが分かります。
namespace Unity.Entities { public static class JobProcessComponentDataExtensions { public static ComponentGroup GetComponentGroupForIJobProcessComponentData(this ComponentSystemBase system, Type jobType); public static void PrepareComponentGroup<T>(this T jobData, ComponentSystemBase system) where T : struct, IBaseJobProcessComponentData; public static void Run<T>(this T jobData, ComponentSystemBase system) where T : struct, IBaseJobProcessComponentData; public static JobHandle Schedule<T>(this T jobData, ComponentSystemBase system, JobHandle dependsOn = default(JobHandle)) where T : struct, IBaseJobProcessComponentData; public static JobHandle ScheduleSingle<T>(this T jobData, ComponentSystemBase system, JobHandle dependsOn = default(JobHandle)) where T : struct, IBaseJobProcessComponentData; } }
実は、インターフェースに拡張メソッドが定義できるの知らなかったので驚きでした。
意外と色々なところで使えそうなテクニックなので使っていこうと思います。
まとめ
ECSのシステム生成について見てきました。
データを定義し、小さく分割したシステムを生成し、それらを連携させて処理をしていく、というのが感じ取れたのではないでしょうか。
既存のGameObjectとコンポーネントを用いた設計とはかなり違いがあるため最初は色々戸惑いそうですが、物量が必要なゲームの場合は必須となる機能なのは間違いないと思います。
まだプレビュー版なので色々とドラスティックに仕様が変わったりしていますが、今後も情報を追っていって、正式リリースした暁にはすぐに使い始められるようにしておきたい機能ですね。
ECSをそろそろ触ってみる ~ECS入門 シーンにオブジェクトを描画編~
概要
この記事は、Unity Advent Calendar 16日目の記事です。
TwitterのTLを見ているとECSを触ってなにかした、みたいのがよく流れてきていて流石にそろそろ触っておきたいなーと思ったので簡単にまとめてみました。
(Advent Calendarのネタがないから急遽手を出したわけじゃありません)
今回は「シーンにオブジェクトを描画編」ということで、シンプルに画面にオブジェクトを描画するところまでを書きたいと思います。
いきなり色々やってしまうと内容がブレてしまうかなと思ったので。
今回の内容についてはGithubにアップしているので、動作するものを見たい方はダウンロードして見てみてください。
ECSとは
まずは簡単に。
ECSとは、Unityが新しく導入を進めている新しいシステムです。
ちなみに「Entity Component System」の頭文字を取って「ECS」です。
ものすごく乱暴な言い方をすれば、処理負荷の高い既存のGameObjectの仕組みをイチから見直して高速化を達成するための仕組み、というような感じです。
詳細については以下のテラシュールブログさんの記事を見るといいと思います。
少しだけ言葉を引用させていただくと、
コンポーネント志向に変わる新しいアーキテクチャパターンです。
と書かれています。
これは、今のコンポーネント指向、オブジェクト指向とは異なる「データ指向」のアーキテクチャを意味しています。
データ指向については以下のCygamesの記事が詳細に解説されています。
データ指向設計 | Cygames Engineers' Blog
データ指向設計とは
少しだけデータ指向設計について。
なぜこれを書くかというと、ECSを利用・理解する上でこの知識は必須となりそうだなと感じたからです。
まぁそもそも、この思想をベースにしているので当たり前と言えば当たり前ですが。
データ指向設計とは、今までのオブジェクト指向などと同じように「設計パターン」です。
そして着目するのが「データ」である、というのが大きな特徴です。
オブジェクト指向はデータではなく、あくまで表現したい「オブジェクト」を主体に考えます。
そしてそれに紐づくデータと振る舞いをセットにして表現します。
一方、データ指向では「コンピュータが扱いやすい形としてのデータ」に着目し、それを元に設計、実装していくパターンです。
なぜデータに着目?
オブジェクト指向は人間がイメージしやすい形でプログラムを書いていくことができるので理解しやすい部類でしょう。(色々解釈などによる議論とかは見ますが)
しかし、コンピュータは「オブジェクト」という概念で物を見るのではなく、あくまでバイナリ表現されたデータを、それがなにかを考えずに黙々と処理していきます。
つまり、オブジェクトごとにまとめられたデータというのは、コンピュータからはまったく関係ない・・・どころか、作業効率の邪魔になり得ます。
実際の例で考えてみると、例えばこう考えてみてください。
あなたは自動販売機に飲み物を補充している店員だとします。
そして補充用の箱には「キリン」とか「サントリー」とか「明治」とかメーカーごとに商品が分けられて入れられています。
しかし、補充する側としては「今補充したい飲み物」だけを詰めてくれた箱があったほうが効率がいいですよね。
例えばコーヒーを補充しているのに、水やら別のものが箱に入っているとより分けて補充しなければなりません。
データ指向はまさにこの「補充したい飲み物だけ」を提供する形にデータを整形して処理するもの、と考えることができます。
こうすることによってCPUが効率よく処理することができるようになるというわけなんですね。
キャッシュミスを減らして効率化
なぜ効率が良くなるかというと、CPUには以下に示すようにいくつかのキャッシュシステムを備えています。
そしてそのキャッシュには一定の塊(キャッシュライン)でデータが読み込まれそれを利用します。
その読み込まれた塊のデータの中に、次に計算するデータが含まれている場合は計算をすばやく行うことができます。
(これをキャッシュヒットと言います)
しかしもしその中に目的のデータがなかった場合は、改めてメモリからキャッシュにデータを読み込む必要があります。
(これをキャッシュミスと言います)
つまり、前述のように「必要なデータを揃えておく」ことによってこの「キャッシュヒット」を期待することができ、逆にそうでない場合は頻繁に「キャッシュミス」が発生することになってしまいます。
ちなみにキャッシュミスによってどれくらい差が出るかですが、CPUとメモリの関係について見てみましょう。
ここでのメモリは「大容量メモリ」、つまり一般的に言われているメモリです。(最近だと16GBとか、32GBとか積んでるあれです)
しかしCPUからは「とても遠い」存在なんですね。
そのため、CPUが扱いやすい距離にある位置にも少量のメモリが置かれます。
これをキャッシュと呼び、L1キャッシュ、L2キャッシュなどと呼びます。(場合によってはL3キャッシュもあるものも)
さて、どれくらい距離に差があるかと言うと。
Cygamesの記事から引用させていただくと以下の表のようになります。
| 種類 | サイズ | レイテンシ |
|---|---|---|
| L1キャッシュ | 32KB - 128KB | 3 - 4サイクル |
| L2キャッシュ | 4MB - 20MB | 20 - 40サイクル |
| メインメモリ | 4GB - 32GB | 200サイクル |
※ サイクルとは、大雑把に言うとCPUがひとつの命令を実行する単位。
これを見てもらえば、どれくらい「距離に差がある」のかがイメージできるかと思います。
メインメモリへのアクセスに要する時間の間に、200命令くらいが実行可能、ということなんですね。
イメージ的にはL1キャッシュが机の上、L2キャッシュが部屋の本棚、メインメモリが近くの本屋、くらいの差です。
そりゃ処理が遅くなるわけですよね。
こうした、実際の内部構造的にどういう感じで最適化されるのか、なぜそれが必要なのかは前述のCygamesの記事を読んでみてください。
登場人物
ECSは新しい概念となるため、既存のUnityの仕組みをひとつひとつ置き換えながら、というのはむずかしそうです。
今回ははまずセットアップから始めて、シーンにメッシュを表示する流れまでを書きたいと思います。
その中で登場するいくつかの機能を紹介しておきましょう。
| 名称 | 意味 |
|---|---|
| Entity | エンティティ。GameObjectに変わる「単位」を表す |
| ComponentData | Entityに格納するデータ |
| ComponentSystem | 実際の処理 |
| Group | ComponentSystemが要求するComponentDataのグループ |
ちなみにこれらの、既存の仕組みとの紐付けですが、上のテラシュールブログさんの記事から引用させていただくと以下のようになるみたいです。
この用語ですが、UnityのGameObject / Componentを差し替えるものだけあって、少し近いところがあります。物凄い大雑把に言ってしまえば、以下のモノと一致します。
ComponentSystemがUpdateメソッドに該当するんですね。
ちなみに、ComponentSystemはいくつかのシステムを作ることができ、それぞれ目的のデータ構造を定義してそれを効率よく計算させることができます。
最後のGroupはまさにこの「システム」に渡すためのデータ構造をグループ化したものとなります。
これは前述の通り、新しいアーキテクチャである「データ指向」に依るものなので既存の仕組みにはない概念となっています。
導入方法
さて、まずは導入方法から。
ECSはまだまだ実験段階のため、正式には導入されていません。
そのため、導入するためには「Package Manager」から明示的にインストールする必要があります。
メインメニューから、「Window -> Package Manager」を開くと以下のようなウィンドウが表示されます。

そして「All」タブの中から「Entities」を選択してインストールします。
またECSは、.NET4.xを必要とするため「Player Settings」の「Scripting Runtime Version」を「.NET 4.x Equivalent」に変更します。
これで準備が整いました。
あとは通常通りコードを書いていくことができます。
ECS Hello World
さぁ、ここからが「Hello World」です。
そして事実、ECSでは「World」というクラスがあり、これがシステム全体を管理する役割を担っています。
ということで、ものすごくざっくりと、画面にメッシュがひとつだけ描画されるサンプルコードを見てみましょう。
using System.Collections; using System.Collections.Generic; using UnityEngine; using Unity.Entities; using Unity.Transforms; using Unity.Rendering; public class SimpleECSTest : MonoBehaviour { [SerializeField] private Mesh _mesh; [SerializeField] private Material _material; private void Start() { World world = World.Active; EntityManager entityManager = world.GetOrCreateManager<EntityManager>(); // Prefabを作成 Entity prefab = entityManager.CreateEntity( ComponentType.Create<Position>(), // 位置 ComponentType.Create<Prefab>() // Prefab(これがついているEntityはSystemから無視される) ); // 描画用のComponentを追加 entityManager.AddSharedComponentData(prefab, new MeshInstanceRenderer { castShadows = UnityEngine.Rendering.ShadowCastingMode.On, receiveShadows = true, material = _material, mesh = _mesh }); // Prefabをインスタンス化 entityManager.Instantiate(prefab); } }
とてもシンプルなコードですね。これを実行すると以下のようにシーンにひとつだけオブジェクトが表示されます。

(MeshとMaterialはインスペクタから適当なものをセットしています)
コードはそこまで多くないので、ひとつひとつ順を追って見ていきましょう。
全体を管理する「World」クラス
冒頭ではWorldクラスを変数に格納しています。
World world = World.Active;
World.Activeにはデフォルトで生成されたワールドが保持されています。
しかしこれは、後述するように、デフォルトワールドの生成を抑止することもできます。
意図しないシステムが可動して無用な負荷を生まないためにも、実際にはオフにすることが多くなると思われます。
しかしまずは、必要最低限のもので描画まで実現するためにサンプルではデフォルトワールドはオンで説明します。
エンティティを生成する準備
デフォルトワールドはWorld.Activeに格納されています。
が、これは上書きすることができるので、現在メインで作業中の、くらいの感じで捉えておくといいかと思います。
ワールドが取得(あるいは生成)できたら、以下のフローによってエンティティ(ECSの単位)を生成します。
生成フロー
EntityManagerを生成(or 取得)する- アーキタイプ(
EntityArchetype)を定義する - アーキタイプを元にエンティティ(
Entity)を生成する - エンティティにコンポーネントデータを設定する
- セットアップが終わったエンティティをインスタンス化する
このフローを踏むことによって、無事にシーンにエンティティが表示されるようになります。
さて、上記フローが一体なにをしているのかというと。
アーキタイプの定義によって、エンティティに必要なデータ構造を定義します。
データ指向のための「設計」
「データ指向」がベースなので、まさにこのデータの設計をしているわけですね。(データのアーキテクチャ)
そしてデータの設計が済んだら、それをベースにエンティティを生成します。
オブジェクト指向で言うとクラスを定義、に近いイメージでしょうか。
(アーキタイプの設計は、オブジェクト指向だとコードを書く前の設計段階に近いかもしれません)
エンティティが生成できたら、次に行うのはそのエンティティの初期値の設定です。
設定はEntityManagerのメソッドを通して設定していきます。
セット用メソッドの第一引数に、生成したエンティティを渡してセットアップしていきます。
(このあたりはC言語っぽいイメージがありますね)
設計を元にしたインスタンス化
そして初期値の設定が終わったらいよいよインスタンス化です。
これもまたEntityManagerのInstantiateメソッドを利用してインスタンス化します。
こうすることで晴れて、エンティティがワールドに誕生することになります。
ECSを利用してエンティティを画面に表示するだけなら以上です。
意外と拍子抜けするほど簡単ですね。
ただ実は大事な概念がまだ説明されていません。
それが「ComponentSystem」です。
しかしこれは、デフォルトワールドではすでにセットアップ済みで、エンティティの設定とインスタンス化をするだけでワールドに誕生させることができます。
とはいえこれではECSを使いこなすことはむずかしいです。
ということで、次は「ComponentSystem」について解説します。
自前Worldの生成とComponentSystem
さて、最後に書くのは「自前World」の作成と「ComponentSystem」についてです。
前述のように、なにもしないとデフォルトワールドが生成された状態になります。
そしてそのワールドには、現在定義されているすべてのシステムがすでに登録済の状態となっています。
ただ、指摘したように基本はオフにするのが通常のフローになるかなーと思っています。
なので実践で使う場合はワールドを自作し、必要なシステムを自分でセットアップする必要があります。
ということで、ワールドの生成と(描画だけを行う最低限の)システムのセットアップについて、コード断片を載せます。(コード見たほうがイメージ湧きやすいかなと思うので)
必要なシステムの登録(生成)
では自作ワールドを作成して描画に必要なシステムの登録をするところから見てみましょう。
// ひとまず、デフォルトのワールドを削除する // // ※ Player SettingsのDefine Symbolsに // 「UNITY_DISABLE_AUTOMATIC_SYSTEM_BOOTSTRAP」を指定しても // デフォルトワールドの生成を抑えられる World.DisposeAllWorlds(); _gameWorld = new World("GameWorld"); // あとからアクセスしやすいように、World.Activeにも設定しておく。 // ※ しなくても大丈夫 World.Active = _gameWorld; // デフォルトで用意されているTransformSystem _gameWorld.CreateManager<EndFrameTransformSystem>(); // デフォルトで用意されている描画を行うためのシステム「MeshInstanceRendererSystem」の補助クラス _gameWorld.CreateManager<RenderingSystemBootstrap>(); // EndFrameTransformSystemなどを先に生成すると、自動的にEntityManagerが生成されるので、GetOrCreateで取得する EntityManager entityManager = _gameWorld.GetOrCreateManager<EntityManager>();
描画に必要なものとして以下の2つのシステムを登録しています。
EndFrameTransformSystemRenderingSystemBootstrap
なお、RenderingSystemBootstrapは描画のシステムであるMeshInstanceRendererSystemの補助クラスとなっているようです。
そして最後に、エンティティ周りを管理するEntityManagerを「取得」しています。
これだけGetOrCreateしているのには訳があります。
実はEndFrameTransformSystemを登録すると内部で自動的にEntityManagerが登録されるようです。
おそらくですが、内部でエンティティ周りの設定などを行うシステムの場合は自動的に生成されるのではないかと思います。
そのため、Createしてしまうと「すでに登録済み」というエラーが発生してしまいます。
エラー内容↓
ArgumentException: An item with the same key has already been added. Key: Unity.Entities.EntityManager
エンティティを作成する
システムの設定が完了したら、前段で取得したEntityManagerを利用してエンティティのセットアップ、生成を行います。
こちらもまずはコードを見てもらうのが早いでしょう。
EntityArchetype archetype = entityManager.CreateArchetype(
// ComponentType.Create<LocalToWorld>(), // Positionなどがあるとデフォルトシステムなら自動で追加してくれる
ComponentType.Create<Position>(),
ComponentType.Create<Rotation>(),
ComponentType.Create<MeshInstanceRenderer>()
);
// アーキタイプを元にエンティティを生成する
Entity entity = entityManager.CreateEntity(archetype);
// Rendererを設定
entityManager.SetSharedComponentData(entity, new MeshInstanceRenderer
{
mesh = _mesh,
material = _material
});
// Transform関連の情報を設定
entityManager.SetComponentData(entity, new Position
{
Value = new float3(0, 0, 0)
});
entityManager.SetComponentData(entity, new Rotation
{
Value = Quaternion.Euler(0f, 180f, 0f)
});
// インスタンス化
entityManager.Instantiate(entity);
コード的には、デフォルトワールドを利用してエンティティを表示したときとほとんど変わりがありませんね。
そして最後でエンティティをインスタンス化しています。
ワールドを有効化する
さあ、これですべてセットアップが終わりました。
が、実はこれだけだとワールドは動作しません。生成しただけでは動かないんですね。
ということで、動作するように有効化します。
// イベントループにワールドを登録する ScriptBehaviourUpdateOrder.UpdatePlayerLoop(_gameWorld);
有効化自体はシンプルです。
ScriptBehaviourUpdateOrderのUpdatePlayerLoopメソッドを利用してアップデートループに登録するだけです。
これで自作ワールドが動きはじめ、エディタを再生すると画面にメッシュが表示されるようになります。
まとめ
今回は以上です。
もう少し実践的に利用する作りについては別記事で書きたいと思います。
まずは自作ワールドを生成し、システムの登録を経てオブジェクトを表示するシンプルな例を示しました。
ECSの作法に慣れれば、あとは専用のシステムなどの制作を通してECSを自由に扱えるようになるはずです。
その他Tips
基本的なECSの使い方と概念の説明は以上です。
あとは、知っておいたほうがいいTipsなどを簡単にまとめておきます。
デフォルトのワールドを生成させないようにする
前述のように、デフォルトのワールドを最初から生成しない方法があります。
それは、「Player Settings」の「Scripting Define Symbols」に以下のシンボルを定義することで無効化することができます。
UNITY_DISABLE_AUTOMATIC_SYSTEM_BOOTSTRAP
以下のように設定する。
生成しても、それを消すこともできます。
以下のようにするとすべてのワールドを破棄することができます。
World.DisposeAllWorlds();
ECSで構築された「世界」を見る
ECSで構築された世界は、通常のシーンのヒエラルキーには表示されません。
前述の青い球体がシーンビューには存在していても、ヒエラルキーにはなにもない状態となっています。
しかしそれでは色々と開発が大変になってしまうので、それを見る方法があります。
メインメニューの「Window > Analysis > Entity Debugger」を起動することで現在のシステムとエンティティを確認することができます。
これを開いて実行すると以下のように、システムとエンティティのリストを見ることができます。
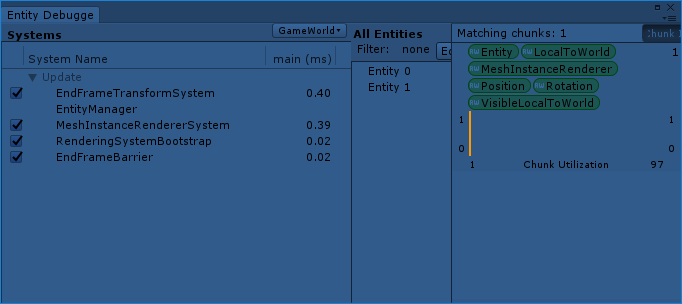
その他ハマりどころ
まだまだ策定途中、実装途中な感じのECS。
そのため仕様変更なども比較的頻繁に行われているようで、調べて出てきた情報がすでに古い、なんてこともあります。
色々ぷちハマりしたところをメモとして残しておこうと思います。
TransfdormMatrixはなくなった
Twitterでつぶやいたところ、以下のようにコメントもらいました。
TransformMatrixは大分前に消えてますね。。
— mao (@TEST_H_) 2018年12月13日
(確かpreview8以降だったか...少しうろ覚えですが...😇)
それ以降では代わりにLocalToWorldと言うComponentDataに置き換わっているという認識です👀
確かに、TransformMatrixよりもより「データ感」のある名称に変更されたということでしょう。
TransformSystemは抽象クラス
これ、もしかしたら途中でそうなったのかもしれませんが。
調べているときに出てきたコードをそのまま書いていたらエラーが。
どうやらTransformSystemは抽象クラスで、実際に利用する場合はその派生クラスであるEndFrameTransformSystemを利用する必要があるとのこと。
(あるいは自作する場合はこれを継承する)
EntityManagerは自動で生成される
システムの説明のときにも触れましたが改めて書いておきます。
前述のEndFrameTransformSystemを先に生成すると、内部的にどうやら自動的にEntityManagerが生成されるようです。
そのため、そのあとに以下のようにセットアップを行おうとするとすでに生成されてるよ! っていうエラーが出ます。
_world.CreateManager<EndFrameTransformSystem>();
EntityManager entityManager = _world.CreateManager<EntityManager>(); // => ここでエラー
エラー内容はこんな感じ↓
ArgumentException: An item with the same key has already been added. Key: Unity.Entities.EntityManager
なので最初に生成するか、あるいはGetOrCreateで取得してあげるとうまくいきます。
EntityManager entityManager = _world.GetOrCreateManager<EntityManager>();
参考にした記事
SteamVR SDK2.0以降でViveトラッカーを適切にアサインする
概要
Kunclesが手元に届いたということもあって、SteamVR SDK2.0について本腰を入れて調べてみようと思い立ちました。が、そもそも以前から適切にViveトラッカーを認識させられず、結局1.0を使うか騙し騙しトラッカーを使っていた状況でした。
そこで、まずは2.0でViveトラッカーを使えるようにしようと奮闘したメモです。
先に結論を書いておきますが、SteamVR SDK側の問題でβ版なら動きました。(おいッ)
なので、ここでまとめていることはおそらく近いうちに対応がされてあまり意味がないものになるかもしれませんが、困っている人もいるかもしれないので記事にしておきます。
そもそもの問題点
そもそもの問題点として、SDK1.0のときは適当にオブジェクトを追加してTrackedObjectコンポーネントとかを適当に設定してマネージャに登録、とすることですぐに認識させることができました。
が、SDK2.0からマネージャ的なものがなくなり、同梱されているPrefabを見てみるとどうやらSteamVR_Behaviour_Poseというコンポーネントで「どのコントローラか」を指定する形になっていました。
Any / LeftHand / RightHandしかない・・・?
インスペクタに表示される「Input Source」を見ると、Any、LeftHand、RightHandしか見当たらない・・・。
トラッカーはどう指定したらいいの?
Manage Vive Trackersで管理
色々探していたら、SteamVRのメニューの「デバイス > Manage Vive Tracker」という項目が。

起動してみると、以下のような設定画面が開きました。
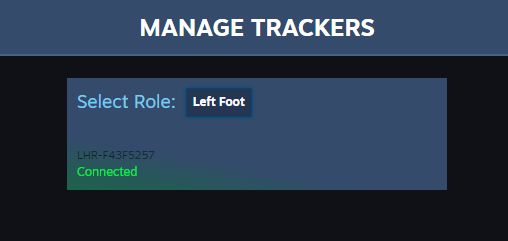
Select Roleで役割を設定
上記画像のように、「Select Role」という項目があり、そこから役割を指定する様子。
いくつか項目がありましたが、フルボディトラッキングを想定しているのか、Footとかがリストされてました。
とにかくなにかしらで指定できればいいので、ひとまずLeft Footを選択。
設定する箇所が見当たらない・・・
やっとこれで役割を指定できたから、あとはPose情報をこのLeft Footを指定したら行けるのでは?
という思いで設定を探すも見つからず。
上にも書いたように、Any、LeftHand、RightHandしかリストにはない。(どういうことだってばよ)
色々なワードで検索をかけていくうちにひとつのissueが目に入りました。
issueの内容を見てみると、コントローラは動いてるし、SteamVRのホーム画面とか(つまりUnity以外の場所)ではちゃんとトラッカー認識してるのに、Unityだと出てこないんだけど?
っていうもの。
完全に自分と同じ状態です。
それへの回答が
We've got some more extensive tracker support coming in the next version. I'll be releasing a beta soon that provides better access to this functionality. I'll update here when I release that.
次のバージョンでサポートするとのこと。ひとまずβ版でリリースするよと。(トラッカーはすでに世に出てるんだから、そこも対応してから出してほしかった・・・(´・ω・`))
そしてβ版のリリースは以下でされていました。
改めてこちらを入れ直して見たところ、ちゃんとLeft Footなどがメニューにあることを確認。
これを指定したところ、しっかりとViveトラッカーが認識されました。(コントローラも含めて全部ちゃんと動いた!)
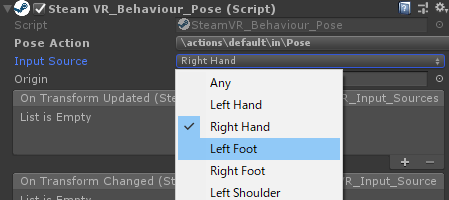
今、トラッカーをベースにコンテンツを作っているので、やっとStemaVR SDK2.0のほうでもトラッカーを使ったコンテンツが問題なく作れそうです。
点と凹多角形の内外判定を行う
概要
凹多角形の内外判定を行いたく、以下の記事を参考にUnityで判定処理を書いたのでそのメモです。
実際に実装した動画です。ちゃんと内外判定が出来ているのが分かるかと思います。
凹多角形の内外判定、意外とシンプルにできるんだなー。外側のときは偏角の合計が0になるっていうのも興味深い。 pic.twitter.com/phBZIrKf3T
— edom18@AR / MESON (@edo_m18) 2018年11月26日
判定の考え方
参考にした記事によると、内外判定は以下のふたつが用いられることが多いそう。
- Crossing Number Algorithm
- Winding Number Algorithm
Crossing Number Algorithm
Crossing Number Algorithmは、大雑把に言うと、調査点から水平方向に(つまりX軸方向に)線を伸ばし、多角形の辺との交差回数をカウントするものです。
ちなみに水平方向の線は半直線で、調査方向を定めてそちらの方向に伸ばしたものとのみ判定を行います。
図にすると以下のような感じです。

(無駄にiPad ProとApple Pencilで図を書いてみたw)
見てもらうと分かる通り、調査点が多角形の内側にある場合は交差回数は奇数回、外側にある場合は偶数回となることが分かるかと思います。
(ただし、水平線がどれかの辺と平行、あるいは多角形の頂点上にある場合は誤判定してしまうのでそれも考慮しないとなりません)
非常にシンプルなアルゴリズムですね。
ただ、自己交差をしている多角形の場合は正常に判定できないようです。
※ 自己交差とは、辺がどこかで交差してしまっていることを指します。
Winding Number Algorithm
もうひとつのアルゴリズムは「Winding Number Algorithm」です。
こちらは、調査点から見て、多角形の各頂点をぐるっと周回して得られる角度の合計がどうなるかで判定を行うものです。
参考にした記事から引用させていただくと以下のように説明されています。
Winding Number Algorithmは、点Pを中心に多角形Tの辺を順番になぞっていった時に点Pの周りを何回回転するかを計算し、その数(
)によって内側・外側の判定を行います。
この時、であれば多角形Tは点Pを取り囲んでいることになるので、点Pは多角形Tの内側にいると判定します。逆に、点Pが多角形Tの外側にいると判定されるのは
の時だけです。
※ 余談ですが、「Winding」には「巻き取る」とか「うねり」という意味があるようです。
そして今回実装したのはこちらのアルゴリズムです。
なお、こちらのアルゴリズム、「角度」の算出にが出てくるため、調査対象の点や多角形の頂点数が多くなると処理負荷が高まります。
参考にした記事では、最初の「Crossing Number Algorithm」を少し拡張したような別の方法での実装方法も紹介されていました。
以下では、Unityで両方実装したので双方について、Unityでの実装をベースに解説したいと思います。
角度を利用したアルゴリズムの実装解説
「とある点」が凹多角形の内側にあるのか外側にあるのかの判断はとてもシンプルです。
「とある点」と凹多角形の各頂点との成す角の合計が0かそれ以外か、で判定することができます。
※ なお、ここでの角については時計回りを正、反時計回りを負としています。つまり符号付き角度で考えることが重要です。(参考にした記事では反時計回りを正としていましたが、ここは多分、決めの問題です。今回のサンプルでは時計回りを正として実装しました)
まずはシンプルに三角形について考えてみましょう。(凹多角形ではないですが、イメージを掴みやすくするために単体で考えます)
以下のように、三角形の内側に点がある場合、それぞれの頂点と「とある点」とで辺を作り、その成す角(偏角)について考えてみます。
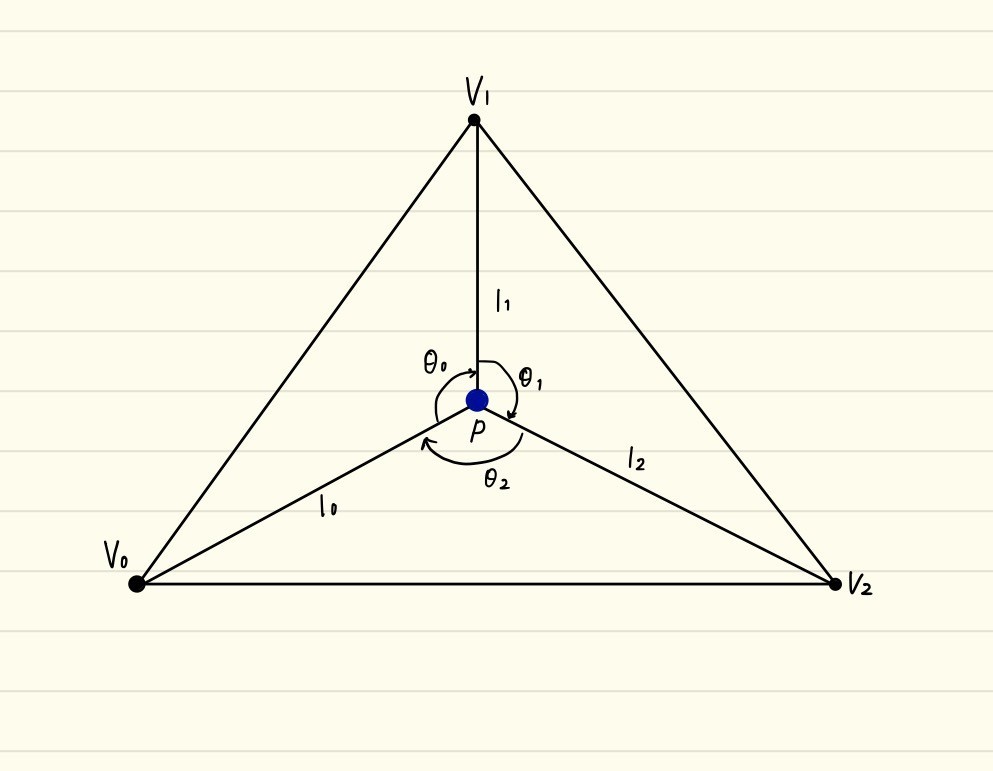
を合計すると360度になるのが分かります。
角の作り方は点と凹多角形の各頂点とを結び辺を作ります。
頂点を()としたとき、点
とで作る辺を(
)とします。
偏角は
とが成す角となります。そしてそれを合計するので、
さらに、1周は360度(=)なので、
で割ることで「何周したか」を計算することができます。まとめると、
と表すことが出来ます。
さて、同様にして四角形でもやってみましょう。
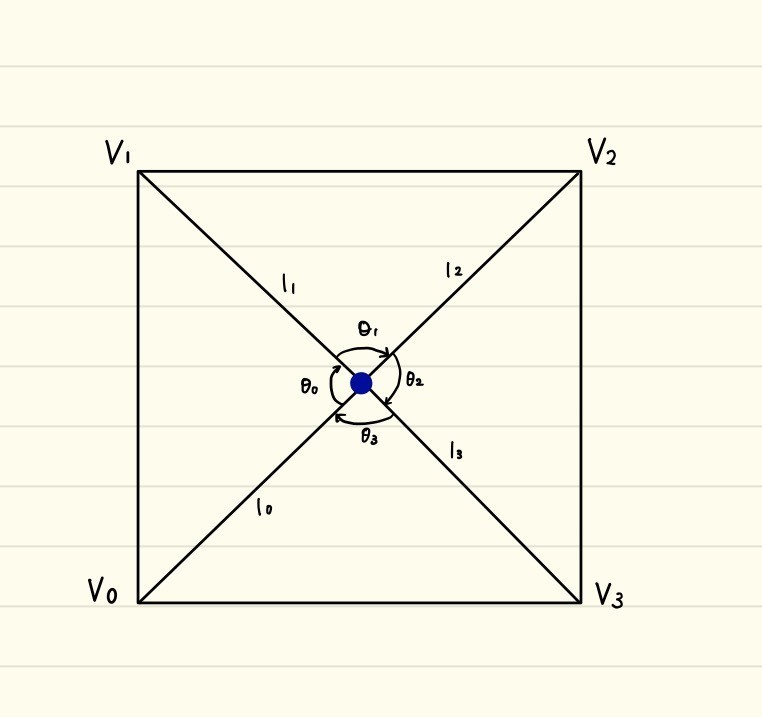
確かに四角形でも360度になることが分かります。
では今度は「とある点」を外側に出して同様の計算をしてみましょう。
すると、以下の図のようにきれいに角度の合計が0にるのが分かるかと思います。
(矢印の向きが違うのは符号付き角度を表しています)
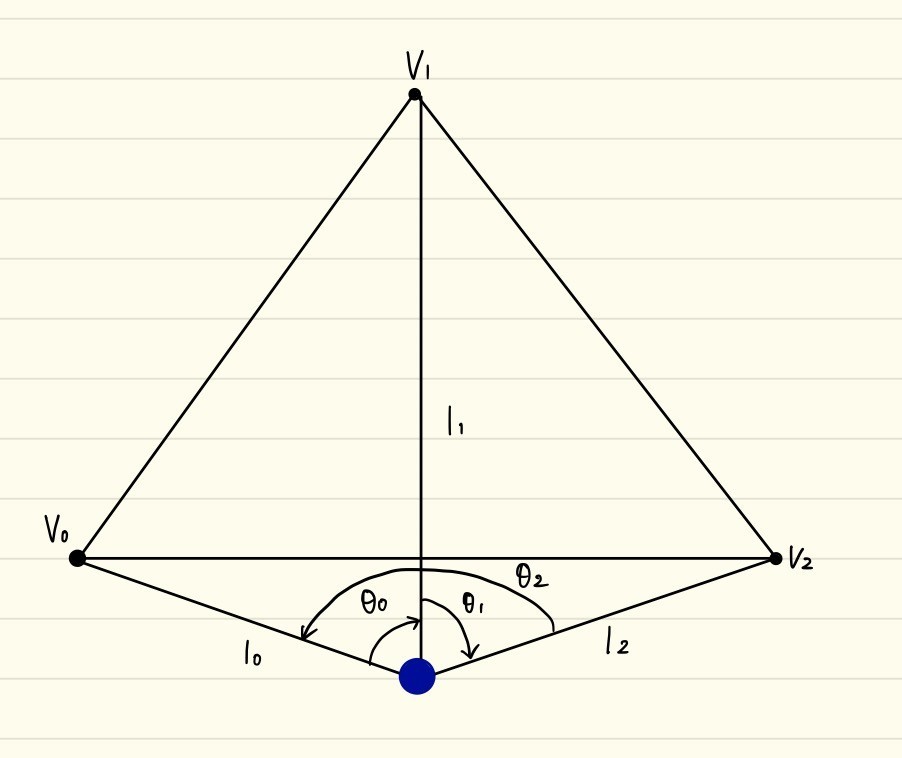
この事実を利用して、凹多角形の外側に点がある場合は偏角の合計が0の場合は外、それ以外の場合は内側、として判断します。
ちなみに、参考にした記事では辺が交差している、より複雑な形状についても判定しています。
その場合でも、外側の場合は0、そしてそれ以外の場合は1以上になることもあるようです。
角度を使ったアルゴリズムのソースコード
上記の内容を実際にC#で実装したコードが以下になります。
////// 多角形を構成する頂点リストと対象点とを使って、対象点が多角形内に含まれるかをテストする /// static public class PointInArea { private const float _unit = 1f / 360f; ////// 調査点が多角形の内外どちらにあるかを判定する /// /// 多角形を構成する頂点リスト /// 調査点 /// 多角形が存在する平面の法線 ///調査点が内側にある場合はtrue static public bool _Check(Vector3[] positions, Vector3 target, Vector3 normal) { float result = 0; for (int i = 0; i < positions.Length; i++) { Vector3 l1 = positions[i] - target; Vector3 l2 = positions[(i + 1) % positions.Length] - target; float angle = Vector3.Angle(l1, l2); Vector3 cross = Vector3.Cross(l1, l2); if (Vector3.Dot(cross, normal) < 0) { angle *= -1; } result += angle; } result *= _unit; // 時計回り・反時計回りどちらもありえるため絶対値で判定する return Mathf.Abs(result) >= 0.01f; } }
コードの行数もそれほど多くなく、とてもシンプルに判定できているのが分かるかと思います。
メソッドの第一引数のpositionsが多角形を構成する頂点配列、targetが調査点P、normalは多角形が存在する平面の法線です。
平面法線を使って回転の方向を判定
法線について少しだけ補足します。
法線を必要としているのは、「偏角の向き」を判断するためです。
2辺の角度を求めるには内積を用いて計算するか、UnityであればVector3.Angleによって角度を求めることができます。
しかしその角度は符号がついていません。つまり、「どちら周りか」が分からないのです。
そこで、平面の法線を利用して外積を求めることでどちら周りの角度なのかを判断しているというわけです。
今回の実装では、選択したふたつの辺の外積と面の法線との外積がマイナス方向だった場合は逆回転として扱うようにしています。
浮動小数点誤差などを考慮
そして最後に、計算結果が0より上かを判定基準としています。
が、ここでも少しだけ細かい処理が入っています。
まず、すべてが逆回転の場合、resultの角度はマイナスになります。
が、それは見る角度が反対だっただけで、内外の判定には関係ありません。
なので絶対値を使って判定するためにMathf.Absを使っています。
最後の比較部分ですが、本来なら0であるかどうか、で判定を行いますが浮動少数点の計算誤差によりきれいに0になりません。
そこで、ある程度0に近い値を利用して、それ以上であれば内側、という判定にしています。
角度を利用したアルゴリズムについては以上です。
次は計算コストを軽量化したアルゴリズムでの実装を解説します。
辺との交差を利用したアルゴリズムの実装解説
こちらはまだしっかりと理解しているわけではないですが、参考にした記事から引用させていただくと以下のようになります。
Crossing Number Algorithmと同様に点Pから伸びる水平線
と多角形Tの辺
が交差する数をカウントし、交差する辺が上向きであるか下向きで加算するか減算するかを変えるということです。 つまり、
- 上向きの辺と水平線Rが交差する場合は
を+1
- 下向きの辺と水平線Rが交差する場合は
を-1
とします。 こうすることで、Crossing Number Algorithmに
- ルール5. 上向きの辺と交差する場合、
を+1する。
- ルール6. 下向きの辺と交差する場合、
を-1する。
Crossing Number Algorithmに、方向を持った辺との交差をルールに加えることによってを求めることができる、ということのようです。
まずはソースコードを見たほうが早いと思うので見てみましょう。
辺との交差を用いたアルゴリズムのソースコード
////// 多角形を構成する頂点リストと対象点とを使って、対象点が多角形内に含まれるかをテストする /// static public class PointInArea { ////// 調査点が多角形の内外どちらにあるかを判定する /// /// 多角形を構成する頂点リスト /// 調査点 /// 多角形が存在する平面の法線 ///調査点が内側にある場合はtrue static public bool Check(Vector3[] points, Vector3 target, Vector3 normal) { // XY平面上に写像した状態で計算を行う Quaternion rot = Quaternion.FromToRotation(normal, -Vector3.forward); Vector3[] rotPoints = new Vector3[points.Length]; for (int i = 0; i < rotPoints.Length; i++) { rotPoints[i] = rot * points[i]; } target = rot * target; int wn = 0; float vt = 0; for (int i = 0; i < rotPoints.Length; i++) { // 上向きの辺、下向きの辺によって処理を分ける int cur = i; int next = (i + 1) % rotPoints.Length; // 上向きの辺。点PがY軸方向について、始点と終点の間にある。(ただし、終点は含まない) if ((rotPoints[cur].y <= target.y) && (rotPoints[next].y > target.y)) { // 辺は点Pよりも右側にある。ただし重ならない // 辺が点Pと同じ高さになる位置を特定し、その時のXの値と点PのXの値を比較する vt = (target.y - rotPoints[cur].y) / (rotPoints[next].y - rotPoints[cur].y); if (target.x < (rotPoints[cur].x + (vt * (rotPoints[next].x - rotPoints[cur].x)))) { // 上向きの辺と交差した場合は+1 wn++; } } else if ((rotPoints[cur].y > target.y) && (rotPoints[next].y <= target.y)) { // 辺は点Pよりも右側にある。ただし重ならない // 辺が点Pと同じ高さになる位置を特定し、その時のXの値と点PのXの値を比較する vt = (target.y - rotPoints[cur].y) / (rotPoints[next].y - rotPoints[cur].y); if (target.x < (rotPoints[cur].x + (vt * (rotPoints[next].x - rotPoints[cur].x)))) { // 下向きの辺と交差した場合は-1 wn--; } } } return wn != 0; } }
冒頭ではまず、平面の計算を行いやすくする目的でXY平面へ全頂点を写像したのちに計算を行っています。
それ以後の実装に関しては冒頭の記事を参考にさせていただきました。
最後の点の評価部分については図解してみました。
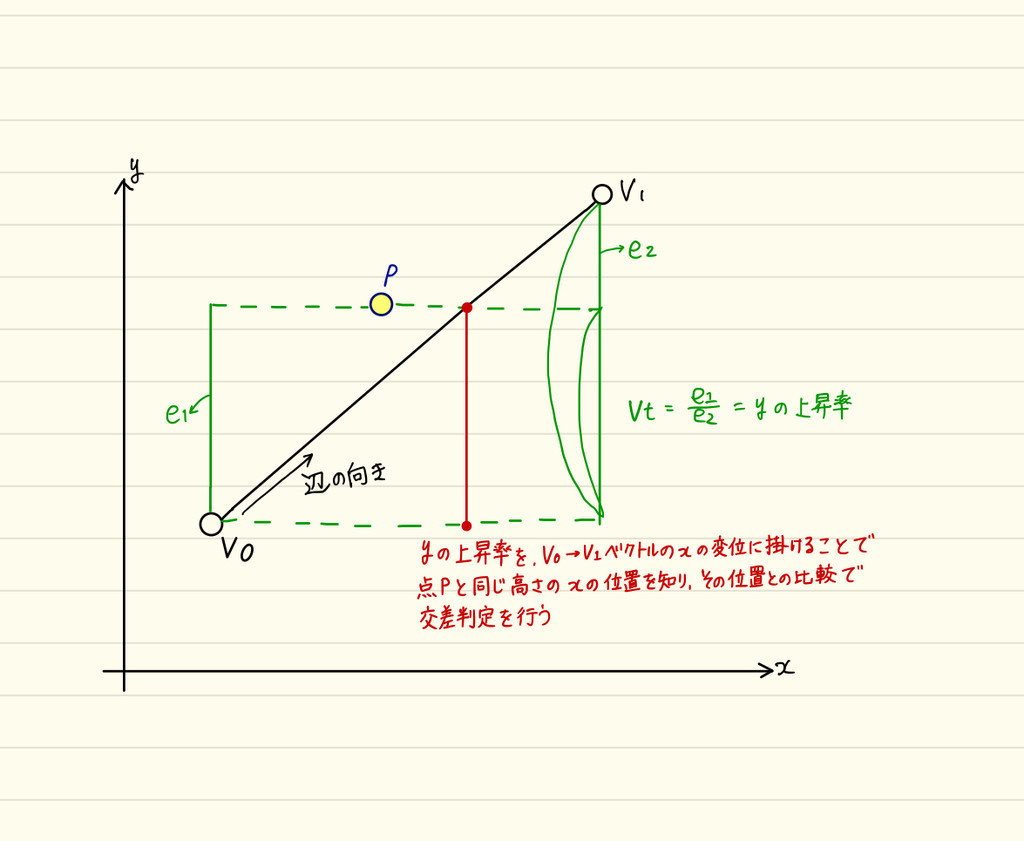
から
が辺の方向ベクトルとなります。
そしてvtは辺ベクトルのy値の上昇率です。
それをxにも適用することで、点と同じ高さの辺の
x位置を知り、それとの比較によって交差判定を行っています。
上の図で言うと、中央付近の赤いラインが該当位置のxの位置を示しています。
この赤いラインと辺ベクトルとの交点が、点と同じ高さの辺上の
x位置となります。
これと比較して、点より右側にあれば交差している、というわけです。
こちらのアルゴリズムでは角度は登場せず、辺との交差回数を増減することによって「何周したか」を判定していることになります。
前述の角度を求めるアルゴリズムと比べて、実際に計測してみたらだいぶ計算負荷に差があったので、基本的には下の実装を利用するのが良さそうです。
ただ、アルゴリズム自体の理解は前述のものを最適化したものなので前者をしっかり把握することが大事だと思います。
モデルの頂点をUV展開した先の位置に任意の絵をテクスチャに描き込む
概要
今回は「モデルをUV展開したあとのテクスチャ空間に絵を描く」仕組みについて書きたいと思います。
ざっくりとしたイメージは以下の動画をご覧ください。
プロジェクタみたいに投影したテクスチャを貼り付けるやつできたー。 pic.twitter.com/HYYjIoSg0x
— edom18@AR / MESON (@edo_m18) 2018年10月29日
動画で行っているのは以下の2点です。
- とある位置からプロジェクタの要領でテクスチャをオブジェクトに投影する
- 任意のタイミング(ボタン押下など)で、プロジェクタで表示しているテクスチャを該当オブジェクトのテクスチャに描き込む
つまり、プロジェクタで投影している絵をスタンプのように貼り付ける機能、というわけです。
また、プロジェクタのようにテクスチャを投影する機能については以前Qiitaに記事を書いたのでそちらを参照ください。
(実装はWebGLですが、基本的な考え方は同じです)
ちなみにこれを使ってコンテンツを制作中。
オブジェクトに「切り傷」をつけられるようになりました。
剣で斬ったところに傷をつける(テクスチャに描き込み)やつできた。 pic.twitter.com/CNzzHbTXi8
— edom18@AR / MESON (@edo_m18) 2018年11月1日
UV展開した位置に描き込む、とは?
UV展開した位置に描き込む、と言われてもいまいちピンと来ない方は以下の動画を見てください。
よし、UV展開したテクスチャの位置に描き込むやつ、アニメーションしているメッシュにも適用できた。ビジュアライズするとちょっと面白いw pic.twitter.com/nccQOUZWOi
— edom18@AR / MESON (@edo_m18) 2018年11月3日
上の動画はUnityのシーンビューを録画したものです。
シーンビューには犬モンスターのモデルと、それにプロジェクタを投影している様子、そしてそのプロジェクタが投影されている頂点位置をUV展開後の座標にマッピングした様子を示しています。
それでなにがうれしいの?
さて、これができるとなにが嬉しいのか。
今回の記事の主題でもありますが、モデルの頂点位置がUV空間に展開した際にどこにあるか、がわかるとその位置に対してGPUを介して描画を行うことで、通常のシェーダで記述した絵をそのままUV空間に転写することができるようになるのです。
そして冒頭の動画ではそれを応用して、プロジェクタで投影した絵をそのまま、モデルで利用するテクスチャに転写している、というわけです。
ことの発端
ことの発端は、以下の動画のようにモンスターに対して切り傷をつけたい、というものでした。
剣で傷をつけるやつ、モンスター(アニメーション付きモデル)でもちゃんと動くようになった。ついでに斬ったときのSEもつけてみたw pic.twitter.com/RKYeKBRmpD
— edom18@AR / MESON (@edo_m18) 2018年11月4日
VRゲームで、実際に剣で斬りつけたときにその場所に傷が残る、というのをやりたかったんですね。
イメージはまさにこのSAOですw
【圧巻】-SAO- ソードアート・オンライン 「スターバーストストリーム」
この戦いのくだりはとてもアツい展開ですよね。
こんな感じで巨大ボスと戦ってみたい。それが今回のことの発端です。
どうやって傷(デカール)をつけるか
やりたいことは明確でしたが、どうやって「斬った場所にだけ」デカールをつけるか、というのが最初の悩みでした。
ちなみにデカールとは、Wikipediaから引用させていただくと以下の意味です。
デカール (decal) は、英語: decalcomania(転写法・転写画)またはフランス語: decalcomanieの略で、印刷・加工工程を終えあとは転写するだけの状態になったシートのことである。
英語の Decal(英語版) には日本で一般的にシール、ステッカー、マーキング、ペイントなどと呼ばれるものも広く含まれる。
要は、メッシュの持つテクスチャとは別に、任意の位置にシールを貼るようにテクスチャを表示する、というものですね。
ただ、シールみたいな任意のテクスチャをそのままペタっと貼るだけならメッシュ上の1点を見つけてテクスチャを書き込んでやればいいのですが、今回やりたかったのは、見てもらうと分かる通り「線」に対してテクスチャを貼りたいのです。
そして色々悩んだ結果、冒頭のようにプロジェクタで投影した位置に描き込めばいけるんじゃないか、と思いつきました。
通常のシェーダのレンダリングをどうテクスチャに展開するか
そう思ってまずはプロジェクタのようにテクスチャをモデルに投影する機能を実装しました。
色々勘違いしていた。ひとまずプロジェクタ風に動くようになった。 pic.twitter.com/e8r4kKvH8k
— edom18@AR / MESON (@edo_m18) 2018年10月26日
無事動いたところで、ふと気づきました。
どうやったら、ワールド空間でレンダリングしているものを、テクスチャ空間でレンダリングしたらいいんだろうか、と。
今回使ったメソッドはGraphics.DrawMeshNow(Mesh mesh, Transform transform)です。
これはその名の通り、メソッド実行後すぐに、設定したマテリアルで対象のメッシュをレンダリングする、というものです。
ドキュメントはこちら↓
しかし、当たり前ですがそのままレンダリングしても、通常のシーンで表示されるのと同じようにレンダリングされてしまって、それをうまくテクスチャ(デカール)として利用することはできません。
つまり、このメソッドでメッシュをレンダリングするが、それはワールド空間ではなく、あくまでそのモデルの「テクスチャ空間」に対してレンダリングしてやる必要があるわけです。
UV値をそのまま頂点位置として利用する
色々悩んでいましたが、実はなんてことありませんでした。
レンダリングパイプラインは頂点シェーダによって頂点変換を経て、ピクセルシェーダによって色を描き込みます。
この「頂点シェーダの頂点位置変換」の際に「UV空間での頂点位置」にうまく頂点を変換できればいいわけです。
ではどうやって。
実はすでにその情報は手元にあります。それはそのまま「UV値」です。
モデルのテクスチャをそのまま見たことがあればピンと来ると思いますが、あれがまさに頂点がテクスチャ空間に展開された「展開図」になっています。
通常のモデルが、UV空間での位置に展開される様子を動画に撮りました。
以下の動画を見てもらうとどういうことか分かりやすいと思います。
モデルの頂点をUV空間に変換するやつ。この書籍の「Projection Spray」っていう章に載ってるやつです。https://t.co/70PO9ettAr pic.twitter.com/cY2GbCJhei
— edom18@AR / MESON (@edo_m18) 2018年11月6日
最初の状態がワールドに置かれたモデル。そしてスライダーを動かすと徐々にUV空間での座標位置に変化していきます。
やっていることはシンプルで、最初(スライダーの値が0の状態)は通常の座標変換、最後(スライダーの値が1の状態)はUV空間での座標位置になるようlerpを使って変化させているだけです。
該当のシェーダコードを抜粋すると以下のようになっています。
v2f vert (appdata v)
{
#if UNITY_UV_STARTS_AT_TOP
v.uv2.y = 1.0 - v.uv2.y;
#endif
float4 pos0 = UnityObjectToClipPos(v.vertex);
float4 pos1 = float4(v.uv2 * 2.0 - 1.0, 0.0, 1.0);
v2f o;
o.vertex = lerp(pos0, pos1, _T);
o.uv2 = v.uv2;
return o;
}
pos0とpos1がそれぞれ最初と最後の頂点位置を格納している変数ですね。
それを、スライダーの値(_T)によってlerpで補間したものを頂点位置としています。
見てもらうと分かると思いますが、なんのことはない、頂点位置をたんにUV値にしているだけ、なんですね。(-1~1の間になるように補正はしていますが)
あとはこれを応用してオフスクリーンレンダリング(RenderTextureへの描き込み)を行えば、適切なテクスチャの位置にピクセルシェーダの結果が保存される、というわけです。
(それをオフスクリーンではなくオンスクリーンでレンダリングしたのが上で紹介した、犬モンスターを使ったビジュアライズ結果の動画です)
なお、上記のシェーダコードは冒頭で紹介した「Unity Graphics Programming vol.2」に掲載されていたものを参考にさせていただいています。
UV2に全頂点を書き出す
さて、上記のコードを見てあることに気づいた人もいるかもしれません。
実はコード内でuv2というパラメータを利用しています。
が、通常UV値はuvに保持されていますよね。
もともとUnityではUVは4つほど予約されており、uv〜uv4まで利用することが出来ます。
今回はその中のuv2を使ったというわけです。
UV2の値はUVと違う?
おそらく、通常はまったく同じ値が設定されています。手元で確認したところ、uvとuv2で同じ結果になりました。
ではなぜ、今回あえてuv2を使っているかというと、それにはちゃんと理由があります。
デフォルトのUV値は、すべての頂点に対して1対1で対応していない場合があります。
UV値はあくまで、どの頂点に対してどのテクスチャをマッピングするか、という情報です。
ただ、似たような場所だったり同じ色を利用したい場合は、異なる頂点に対して同じUVを割り当てることがありえます。
すると、今回実現したかったデカールを再現するには問題になってきます。
というのも、得たいのは全頂点に1対1対応するUVの位置が知りたいのでした。
しかしそれが重複してしまっていては問題になるのは明らかですね。
なのでこれを対処しないとなりません。
UV2に全頂点と1対1対応するUV値を生成する
実はこの機能、Unityに標準で備わっています。
モデルファイルのインスペクタの情報の中に、以下の項目があります。

赤いラインを引いた箇所に「Generate Lightmap UV」とあります。
これにチェックを入れて「Apply」ボタンを押すと、UV2に、全頂点に1対1対応するUVの値が生成されます。
そして犬モンスターから生成されたものは以下のようになります。

そしてもともとのUVの値を表示してみたのが以下です。

だいぶ様子が違いますね。
これが、全頂点に1対1対応するUVを生成する、と書いた意味です。
これを元に、表示と実際にRenderTextureに描き込んだ結果は以下のようになります。


プロジェクタで投影されている位置にしっかりと描き込まれているのが分かるかと思います。
コード抜粋
これを実際に行っているコードの抜粋を以下に示します。
まずはRenderTextureに描き込みを行っているシェーダコードから。
// 頂点シェーダ
v2f vert(appdata v)
{
v2f o;
float2 uv2 = v.uv2;
#if UNITY_UV_STARTS_AT_TOP
uv2.y = 1.0 - uv2.y;
#endif
o.vertex = float4(uv2 * 2.0 - 1.0, 0.0, 1.0);
o.uv = v.uv;
o.uv2 = v.uv2;
float4x4 mat = mul(_ProjectionMatrix, unity_ObjectToWorld);
o.projUv = mul(mat, v.vertex);
#if UNITY_UV_STARTS_AT_TOP
o.projUv.y *= -1.0;
#endif
return o;
}
// フラグメントシェーダ
fixed4 frag(v2f i) : SV_Target
{
// ... 中略 ...
// ------------------------------------------------------
// RenderTextureに描き込まれているテクセルと
// 現在プロジェクタが投影している位置のテクセルとを合成する
fixed4 col = tex2D(_MainTex, i.uv2);
fixed4 proj = tex2Dproj(_ProjectTex, i.projUv);
return lerp(col, proj, proj.a);
}
上記シェーダを使って、以下のようにしてオフスクリーンレンダリングを行います。
/// <summary> /// スタンプの描き込み /// </summary> /// <param name="drawingMat">描き込み用マテリアル</param> public void Draw(Material drawingMat) { drawingMat.SetTexture("_MainTex", _pingPongRts[0]); RenderTexture temp = RenderTexture.active; RenderTexture.active = _pingPongRts[1]; GL.Clear(true, true, Color.clear); drawingMat.SetPass(0); if (_skinRenderer != null) { _skinRenderer.BakeMesh(_mesh); } Graphics.DrawMeshNow(_mesh, transform.localToWorldMatrix); RenderTexture.active = temp; Swap(_pingPongRts); if (_fillCrack != null) { Graphics.Blit(_pingPongRts[0], _pingPongRts[1], _fillCrack); Swap(_pingPongRts); } Graphics.CopyTexture(_pingPongRts[0], _output); }
C#側で行っているのは、まずオフスクリーンレンダリングをするためにRenderTexture.activeを、描き込み用のRenderTextureに差し替えています。
そして描き込みと読み込みそれぞれのRenderTextureをふたつ用意して(ダブルバッファ)、ピンポンするように、現在すでに描き込まれている情報を加味しつつ、新しいテクスチャに投影状態を描き込んでいます。
実際に書き込んでいるのは、コード中央あたりにあるGraphics.DrawMeshNow(_mesh, transform.localToWorldMatrix);の部分です。
直前で、上で示したシェーダを適用したマテリアル(drawingMat)のdrawingMat.SetPass(0);を呼んで、該当シェーダでレンダリングを行うようにしています。
これを描き込みのたびに交互に行うことで何度もスタンプを押すようにテクスチャに内容を描き込むことができる、というわけです。
なお、こちらのコードも冒頭で紹介した書籍を参考にさせていただきました。
該当コードはGithubで公開されているので詳細は以下をご覧ください。
ちなみにひとつ変更点として、書籍ではstaticなメッシュに対して描き込みを行っていたので問題はなかったのですが、今回やりたかったのはモンスターと「戦う」というシチュエーションでした。
そのため、テクスチャを描き込むターゲットはSkinnedMeshRendererによってアニメーションしているメッシュです。
なので、以下のようにして動的にメッシュの状態を更新してから描き込みを行っています。
if (_skinRenderer != null) { _skinRenderer.BakeMesh(_mesh); }
これをしないと、アニメーションしたあとのメッシュではなくデフォルトの状態の位置に描き込まれてしまって微妙に位置がずれてしまうので注意が必要です。
まとめ
今回の、頂点位置をUV座標に展開してRenderTextureに描き込むテクニックは結構色々なところで使えるんじゃないかなーと思っています。
プロジェクタ風の表現について、Unityでの実装は需要があったら書きたいと思いますw(微妙にハマりどころがあった)
ひとまずこれで、やりたいことができそうなのでコンテンツを作っていこうと思います。
Unityでパーリンノイズの実装
概要
今回はパーリンノイズについて書きたいと思います。
以前実装して使ったりしていましたが、しっかりと理論を理解して使ってはいなかったので、改めて、という感じです。
Wikipediaから引用させていただくと、
パーリンノイズ(英: Perlin noise)とは、コンピュータグラフィックスのリアリティを増すために使われるテクスチャ作成技法。擬似乱数的な見た目であるが、同時に細部のスケール感が一定である。このため制御が容易であり、各種スケールのパーリンノイズを数式に入力することで多彩なテクスチャを表現できる。パーリンノイズによるテクスチャは、CGIで自然な外観を物に与えるためによく使われる。
Ken Perlin が Mathematical Applications Group, Inc. で勤務しているときに開発した。彼はこの業績により、1997年、映画芸術科学アカデミーからアカデミー科学技術賞(Technical Achivement)を受賞した。
パーリンノイズは (x,y,z) または (x,y,z,time) の関数として実装され、事前に計算された勾配に従って内挿を行い、時間的/空間的に擬似乱数的に変化する値を生成する。Ken Perlin は2002年に実装を改善し、より自然に見えるようにした(外部リンク参照)。
パーリンノイズは、コンピュータグラフィックスで炎や煙や雲を表現するのによく使われている。また、メモリ使用量が少ないため、メモリ容量が小さい場面でのテクスチャ生成にも使われ、パソコンゲームでのリアルタイムCG生成時にGPU上で使われることが増えている。
実際にレンダリングしてみたのがこれ。Photoshopで「雲模様」ってフィルタ使うと出てくるやつですね。
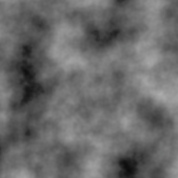
パーリンノイズはいたるところで利用されています。 例えば、以前Unityで実装した「カールノイズ」でも内部的にパーリンノイズを使っていたりします。
Table of Contents
そして今回改めてこれを書こうと思ったのは、最近ハマっているレイマーチングでフラクタル地形を描きたいな、と思ったのがきっかけです。
ちなみにこちらの記事(非整数ブラウン運動)から引用させていただくと、
周波数を一定の割合で増加させる(lacunarity)と同時に振幅を減らしながら(gain)ノイズを(octaveの数だけ)繰り返し重ねることで、より粒度の細かいディテールを持ったノイズを作り出すことができます。このテクニックは「非整数ブラウン運動(fBM)」または単に「フラクタルノイズ」と呼ばれていて、最も単純な形は下記のコードのようになります。
と書かれています。 これはパーリンノイズの振幅と、周波数をオクターブごとに変えたものを重ね合わせて作るノイズです。 (上のJSでの実装も、まさにこのオクターブを重ね合わせて雲のような模様を作っています)
このフラクタル地形をさらに発展させると以下のようなすばらしい映像を、フラグメントシェーダのみで記述することが可能となります。
 https://www.shadertoy.com/view/4sXGRM
https://www.shadertoy.com/view/4sXGRM
目下の目標は上のような海をレンダリングすることです。
なお、今回の記事は以下の記事を大いに参考にさせていただきました。ありがとうございます。
パーリンノイズの考えかた
パーリンノイズは「グラデーションノイズ(勾配ノイズ)」と呼ばれています。
これは後述する、勾配ベクトルを用いたノイズ生成処理に起因しているものと思われます。
パーリンノイズ関数は、0〜1の範囲で値を返す関数です。
ではどのようにしてその値を算出するのでしょうか。
パーリンノイズの値算出
まずは以下の図を見てください。
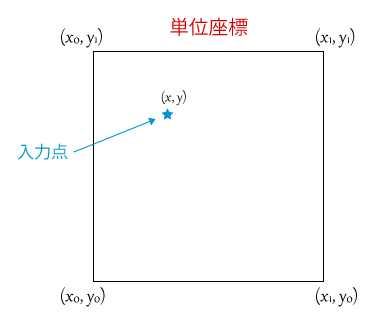
これはパーリンノイズで利用する「単位座標」を図解したものです。
(上記画像は2次元での例ですが、多次元に拡張可能で3次元の場合は図に加えてZの値が入ります)
そして中央やや左上にあるのが入力点の位置です。
つまり、「パーリンノイズ関数への入力」ですね。
(ただし、後述するように0~1でclampされた値となります)
そしてその入力点に対して計算を行い、ノイズとしての最終的な値を算出することになります。
単位座標
なぜ単位座標と呼ぶかと言うと、入力されたx, y, zの値を0〜1の間で繰り返させ、1を超える場合はまた0に戻るように「繰り返し」の状況を作るため「単位」なんですね。
ちなみに擬似コードで示すと以下のイメージです。
[x, y, z] = [x, y, z] % 1.0;
x, y, zの値を1で割った余りを利用することで、0〜1の間で繰り返させるわけです。
疑似乱数勾配ベクトル
単位座標について説明しました。
この単位座標は4つの(3次元なら8つの)勾配ベクトルを持ちます。
この勾配ベクトルは擬似乱数によって生成します。
つまり、勾配ベクトルの方程式に入力された整数に対して、常に同じ結果を返すものです。(なので疑似乱数)
これは、与えられた勾配ベクトル方程式が変わらなければ単位座標が持つ勾配ベクトルは固有の値を持つことを意味します。
以下の図を見てください。
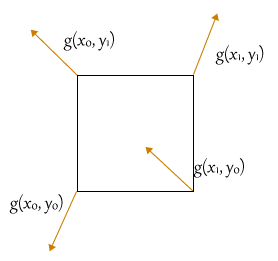
これは、単位座標のそれぞれの頂点に勾配ベクトルを加えた図です。
距離ベクトルを求める
次に、入力点と各頂点からの距離ベクトルを求めます。
距離ベクトルは単純に、入力点から各頂点の位置ベクトルを減算することで求めることができますね。
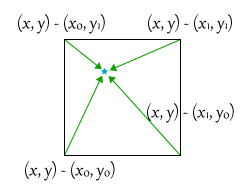
距離ベクトルと勾配ベクトルの内積がノイズに対する影響値
さて、上記で求めた距離ベクトルですが、このベクトルと各頂点の勾配ベクトルとの内積を取ることで入力点に対する各頂点の勾配ベクトルの影響値が算出できます。
なぜ内積を取ると影響値が算出できるのかというと、ベクトルの内積は、言ってしまえばふたつのベクトルが「どれだけ似通っているか」を判断することができるためです。
ちなみに内積の定義は以下のようになります。
そしてもし、ベクトルがまったく同じ方向を向いていたら(つまり平行であったら)、は
となり、結果的に
a.length * b.lengthとなります。
(逆に反対を向いていたら反転し-1が乗算されたものと同じ結果になります)
この影響を図示したものを、参考にさせていただいた記事から引用させていただくと以下のようになります。
加重平均で最終値を求める
これで、各4頂点との影響値を計算することができました。
最後に、この4頂点の勾配ベクトルを加重平均によって求めます。
まず、各4頂点から得られた勾配ベクトルの影響値を以下のように図示します。
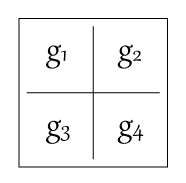
がそれぞれの勾配ベクトルとの内積結果です。
この結果を、それぞれの値の補間を計算し、最終的な値として採用します。
具体的には、疑似コードで表すと以下のようになります。
int g1, g2, g3, g4; int u, v; int x1 = lerp(g1, g2, u); int x2 = lerp(g3, g4, u); int result = lerp(x1, x2, v);
やっていることは、まず横方向の補間を計算し(および
)、その結果をさらに縦方向に補間します。(
の補間)
これで補間した結果の値が求まりました。
フェード関数
さて、実はこれではまだ問題があります。
というのも、上記は線形補間をしてしまったために、補間値が折れ線グラフのようになってしまいます。
しかし冒頭に載せた図はそこまでパキっとしていませんね。
そこで、フェード関数と呼ばれる関数を用いて線形補間の係数自体をなめらかに変換することで実現します。
フェード関数は以下の形の関数です。
6t5 - 15t4 + 10t3
グラフにしてみると以下の図のようになります。
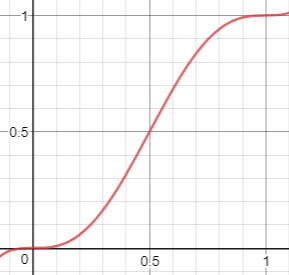
スムーズに変化しているのが分かりますね。
これで、必要な要素が揃いました。
改良版のパーリンノイズ
必要な要素が揃ったと書きましたが、実は改良版のパーリンノイズでは若干異なるアプローチを取っているようです。
ひとつは、勾配ベクトルです。
改良版の勾配ベクトルについてですが、実は正直まだよく理解できていません。
参考にさせていただいた記事から引用すると、
しかしながら、上の図は完全に正確ではありません。この記事で扱っているKen Perlinの改良パーリンノイズでは、これらの勾配は全くの無作為ではありません。立方体の中心点のベクトルから辺に向かって取り出されます。
と書かれています。
上の図というのは本記事でのこの図です↓

図では無作為(ランダム)なように記載されていますが、これが「無作為ではない」というのが引用した文の主張のようです。
そして取り出されるベクトルは以下の12ベクトルになります。
(1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0), (1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1), (0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1)
だいぶ整理されたベクトルの印象を受けますね。
このベクトルについての根拠を、大元の論文(Ken PerlinのSIFFRAPH 2002の論文「Improving Noise」)から引用させてもらうと以下のように記載されています。
The key to removing directional bias in the gradients is to skew the set of gradient directions away from the coordinate axes and long diagonals. In fact, it is not necessary for G to be random at all, since P provides plenty of randomness. The corrected version replaces G with the 12 vectors defined by the directions from the center of a cube to its edges:
ここで言っているのは、ざっくり言うと、勾配ベクトルは、使用している
が十分にランダムなのでランダムである必要はない、ということのようです。
さらに論文ではこう続きます。
Gradients from this set are chosen by using the result of P, modulo 12.
配列の結果から、勾配が選択される、と。
後述する実装例を見てもらうと分かりますが、実際に、計算自体はP配列の結果を元に計算が行われます。
なお、(ここが理解しきれていない点ですが)前段では「距離ベクトルと勾配ベクトルの内積を取る」と説明しました。
しかし、参考にした実装では内積計算を(明示的には)行っていません。
論文をさらに読み進めると以下のように書かれています。
it allows the eight inner products to be effected without requiring any multiplies, thereby removing 24 multiplies from the computation.
乗算を行うことなく、8つの頂点(2次元なら4つ)との内積を得ることができる、と。
このあたりの数学的な理由や原理が理解できていない点です。
しかしながら、「内積を求めてそれを利用する」という「概念」自体は変わっていません。
結局のところ、各頂点と距離ベクトルとの内積を計算しそれを影響値とする、ということ自体は変わらず、その算出方法をより効率的にした、というのが改良版パーリンノイズだと解釈しています。
複数オクターブを利用した表現の拡張
実は今回実装した例では、この「複数オクターブ重ねたノイズ」となっています。
しかしながら、パーリンノイズ自体は前述の説明がすべてです。
これを、さらに「オクターブ」という概念で複数のノイズを生成し、それを合成することでより自然なノイズを生成する、というのが目的です。
ちなみにこの表現を「フラクタルブラウン運動(fractal brownian motion)」と呼ぶようです。
※ おそらく。参考にした記事での実装や、その他の記事を見るに、実装方法はほぼ同じなのでそう解釈しています。
これについては以下の記事を参照ください。
ちなみに、冒頭でも書いたように、これをさらに発展させた「ドメインワープ」という表現を使って波や動く雲の表現をレイマーチングによって実装するのが目下の目標です。
このドメインワープという方法を実装した例がこちら。(あくまで上の記事で紹介されているコードを、必要な部分だけ抜き出して実装したものです)
fBMをfBMで歪めるドメインワーピング。すごい。 https://t.co/8fJCD1wNe3 参考記事: https://t.co/R3ye88Dc1O pic.twitter.com/vEBvtHUrnX
— edom18@AR / MESON (@edo_m18) 2018年10月10日
最終的にはこれを理解して、実際のコンテンツに盛り込めるようにするのが目標です。
なので今回はこのオクターブでの表現については説明を割愛して、次の記事で詳細に書きたいと思います。
[2018.10.18 追記]
Qiitaでドメインワープについての記事を書きました。
ソースコード
using System.Collections; using System.Collections.Generic; using UnityEngine; ///////////// /// Xorshift。擬似乱数生成用に使用する public class Xorshift { private uint[] _vec = new uint[4]; public Xorshift(uint seed = 100) { for (uint i = 1; i <= _vec.Length; i++) { seed = 1812433253 * (seed ^ (seed >> 30)) + i; _vec[i - 1] = seed; } } public float Random() { uint t = _vec[0]; uint w = _vec[3]; _vec[0] = _vec[1]; _vec[1] = _vec[2]; _vec[2] = w; t ^= t << 11; t ^= t >> 8; w ^= w >> 19; w ^= t; _vec[3] = w; return w * 2.3283064365386963e-10f; } } public class PerlinNoise { private Xorshift _xorshit; private int[] _p; public float Frequency = 32.0f; ////// Constructor /// public PerlinNoise(uint seed) { _xorshit = new Xorshift(seed); int[] p = new int[256]; for (int i = 0; i < p.Length; i++) { // 0 - 255の間のランダムな値を生成する p[i] = (int)Mathf.Floor(_xorshit.Random() * 256); } // pの倍の数の配列を生成する int[] p2 = new int[p.Length * 2]; for (int i = 0; i < p2.Length; i++) { p2[i] = p[i & 255]; } _p = p2; } private float Fade(float t) { // 6t^5 - 15t^4 + 10t^3 return t * t * t * (t * (t * 6f - 15f) + 10f); } ////// Linear interpoloation /// private float Lerp(float t, float a, float b) { return a + t * (b - a); } ////// Calculate gradient vector. /// private float Grad(int hash, float x, float y, float z) { // 15 == 0b1111 : Take the first 4 bits of it. int h = hash & 15; float u = (h < 8) ? x : y; float v = (h < 4) ? y : (h == 12 || h == 14) ? x : z; return ((h & 1) == 0 ? u : -u) + ((h & 2) == 0 ? v : -v); } ////// To simplify above function to below. /// // private float Grad(int hash, float x, float y, float z) // { // switch(hash & 0xF) // { // case 0x0: return x + y; // case 0x1: return -x + y; // case 0x2: return x - y; // case 0x3: return -x - y; // case 0x4: return x + z; // case 0x5: return -x + z; // case 0x6: return x - z; // case 0x7: return -x - z; // case 0x8: return y + z; // case 0x9: return -y + z; // case 0xA: return y - z; // case 0xB: return -y - z; // case 0xC: return y + x; // case 0xD: return -y + z; // case 0xE: return y - x; // case 0xF: return -y - z; // default: return 0; // never happens // } // } private float Noise(float x, float y = 0, float z = 0) { // Repeat while 0 - 255 int X = (int)Mathf.Floor(x) & 255; int Y = (int)Mathf.Floor(y) & 255; int Z = (int)Mathf.Floor(z) & 255; // trim integer x -= Mathf.Floor(x); y -= Mathf.Floor(y); z -= Mathf.Floor(z); float u = Fade(x); float v = Fade(y); float w = Fade(z); int[] p = _p; #region ### calulate hashes from array of p ### int A, B, AA, AB, BA, BB, AAA, ABA, AAB, ABB, BAA, BBA, BAB, BBB; A = p[X + 0] + Y; AA = p[A] + Z; AB = p[A + 1] + Z; B = p[X + 1] + Y; BA = p[B] + Z; BB = p[B + 1] + Z; AAA = p[AA + 0]; ABA = p[BA + 0]; AAB = p[AB + 0]; ABB = p[BB + 0]; BAA = p[AA + 1]; BBA = p[BA + 1]; BAB = p[AB + 1]; BBB = p[BB + 1]; #endregion ### calulate hashes from array of p ### float a = Grad(AAA, x + 0, y + 0, z + 0); float b = Grad(ABA, x - 1, y + 0, z + 0); float c = Grad(AAB, x + 0, y - 1, z + 0); float d = Grad(ABB, x - 1, y - 1, z + 0); float e = Grad(BAA, x + 0, y + 0, z - 1); float f = Grad(BBA, x - 1, y + 0, z - 1); float g = Grad(BAB, x + 0, y - 1, z - 1); float h = Grad(BBB, x - 1, y - 1, z - 1); return Lerp(w, Lerp(v, Lerp(u, a, b), Lerp(u, c, d)), Lerp(v, Lerp(u, e, f), Lerp(u, g, h))); } public float OctaveNoise(float x, int octaves, float persistence = 0.5f) { float result = 0; float amp = 1.0f; float f = Frequency; float maxValue = 0; for (int i = 0; i < octaves; i++) { result += Noise(x * f) * amp; f *= 2.0f; maxValue += amp; amp *= persistence; } return result / maxValue; } public float OctaveNoise(float x, float y, int octaves, float persistence = 0.5f) { float result = 0; float amp = 1.0f; float f = Frequency; float maxValue = 0; for (int i = 0; i < octaves; i++) { result += Noise(x * f, y * f) * amp; f *= 2.0f; maxValue += amp; amp *= persistence; } return result / maxValue; } public float OctaveNoise(float x, float y, float z, int octaves, float persistence = 0.5f) { float result = 0; float amp = 1.0f; float f = Frequency; float maxValue = 0; for (int i = 0; i < octaves; i++) { result += Noise(x * f, y * f, z * f) * amp; f *= 2.0f; maxValue += amp; amp *= persistence; } return result / maxValue; } }
これを実際に利用するコードは以下のようになります。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class PerlinNoiseTest : MonoBehaviour
{
[SerializeField]
private GameObject _quad;
[SerializeField]
[Range(1, 16)]
private int _octaves = 5;
[SerializeField]
[Range(0.1f, 64.0f)]
private float _frequency = 32.0f;
[SerializeField]
private float _persistence = 0.5f;
[SerializeField]
private int _width = 512;
[SerializeField]
private int _height = 512;
[SerializeField]
private uint _seed = 1000;
private PerlinNoise _noise;
private PerlinNoise Noise
{
get
{
if (_noise == null)
{
_noise = new PerlinNoise(_seed);
}
return _noise;
}
}
private Texture2D _texture;
private void Start()
{
CreateNoise();
}
private void OnValidate()
{
if (Application.isPlaying)
{
CreateNoise();
}
}
private void CreateNoise()
{
_texture = new Texture2D(_width, _height, TextureFormat.RGBA32, false);
Noise.Frequency = _frequency;
Color[] pixels = new Color[_width * _height];
float fx = 1f / (float)_width;
float fy = 1f / (float)_height;
for (int i = 0; i < pixels.Length; i++)
{
int x = i % _width;
int y = i / _width;
float n = Noise.OctaveNoise(x * fx, y * fy, _octaves, _persistence);
float c = Mathf.Clamp(218f * (0.5f + n * 0.5f), 0f, 255f) / 255f;
pixels[i] = new Color(c, c, c, 1f);
}
_texture.SetPixels(0, 0, _width, _height, pixels);
_texture.Apply();
Renderer renderer = _quad.GetComponent();
renderer.material.mainTexture = _texture;
}
}
これを、シーンに配置したQuadに設定して実行すると以下のような結果になります。

なお、今回のパーリンノイズの実装はGithubにアップしてあります。
シンプル版パーリンノイズ
のたぐすさんの以下の記事で書かれているコードをベースに、最近では簡易版として以下のファイルを作って利用しています。
シンプル版パーリンノイズとカールノイズ
ちなみにカールノイズもよく使うので一緒に入れています。が、やはり負荷が高めなのであまり多様はできません。
#ifndef __NOISEMATH_CGINC__
#define __NOISEMATH_CGINC__
float rand(float x)
{
return frac(sin(x) * 43758.5453);
}
float rand(float2 co)
{
return frac(sin(dot(co.xy, float2(12.9898, 78.233))) * 43758.5453);
}
float rand(float3 co)
{
return frac(sin(dot(co.xyz, float3(12.9898, 78.233, 56.787))) * 43758.5453);
}
float2x2 rot(float a)
{
float s = sin(a);
float c = cos(a);
return float2x2(c, -s, s, c);
}
float noise(float3 pos)
{
float3 ip = floor(pos);
float3 fp = smoothstep(0, 1, frac(pos));
float4 a = float4(
rand(ip + float3(0, 0, 0)),
rand(ip + float3(1, 0, 0)),
rand(ip + float3(0, 1, 0)),
rand(ip + float3(1, 1, 0)));
float4 b = float4(
rand(ip + float3(0, 0, 1)),
rand(ip + float3(1, 0, 1)),
rand(ip + float3(0, 1, 1)),
rand(ip + float3(1, 1, 1)));
a = lerp(a, b, fp.z);
a.xy = lerp(a.xy, a.zw, fp.y);
return lerp(a.x, a.y, fp.x);
}
float perlin(float3 pos)
{
return
(noise(pos) * 32 +
noise(pos * 2) * 16 +
noise(pos * 4) * 8 +
noise(pos * 8) * 4 +
noise(pos * 16) * 2 +
noise(pos * 32)) / 63;
}
/// パーリンノイズによるベクトル場
/// 3Dとして3要素を計算。
/// それぞれのノイズは明らかに違う(極端に大きなオフセット)を持たせた値とする
float3 Pnoise(float3 vec)
{
float x = perlin(vec);
float y = perlin(float3(
vec.y + 31.416,
vec.z - 47.853,
vec.x + 12.793
));
float z = perlin(float3(
vec.z - 233.145,
vec.x - 113.408,
vec.y - 185.31
));
return float3(x, y, z);
}
float3 CurlNoise(float3 pos)
{
const float e = 1e-4f;
const float e2 = 2.0 * e;
const float invE2 = 1.0 / e2;
const float3 dx = float3(e, 0.0, 0.0);
const float3 dy = float3(0.0, e, 0.0);
const float3 dz = float3(0.0, 0.0, e);
float3 p_x0 = Pnoise(pos - dx);
float3 p_x1 = Pnoise(pos + dx);
float3 p_y0 = Pnoise(pos - dy);
float3 p_y1 = Pnoise(pos + dy);
float3 p_z0 = Pnoise(pos - dz);
float3 p_z1 = Pnoise(pos + dz);
float x = (p_y1.z - p_y0.z) - (p_z1.y - p_z0.y);
float y = (p_z1.x - p_z0.x) - (p_x1.z - p_x0.z);
float z = (p_x1.y - p_x0.y) - (p_y1.x - p_y0.x);
return float3(x, y, z) * invE2;
}
#endif