概要
凹多角形の内外判定を行いたく、以下の記事を参考にUnityで判定処理を書いたのでそのメモです。
実際に実装した動画です。ちゃんと内外判定が出来ているのが分かるかと思います。
凹多角形の内外判定、意外とシンプルにできるんだなー。外側のときは偏角の合計が0になるっていうのも興味深い。 pic.twitter.com/phBZIrKf3T
— edom18@AR / MESON (@edo_m18) 2018年11月26日
判定の考え方
参考にした記事によると、内外判定は以下のふたつが用いられることが多いそう。
- Crossing Number Algorithm
- Winding Number Algorithm
Crossing Number Algorithm
Crossing Number Algorithmは、大雑把に言うと、調査点から水平方向に(つまりX軸方向に)線を伸ばし、多角形の辺との交差回数をカウントするものです。
ちなみに水平方向の線は半直線で、調査方向を定めてそちらの方向に伸ばしたものとのみ判定を行います。
図にすると以下のような感じです。

(無駄にiPad ProとApple Pencilで図を書いてみたw)
見てもらうと分かる通り、調査点が多角形の内側にある場合は交差回数は奇数回、外側にある場合は偶数回となることが分かるかと思います。
(ただし、水平線がどれかの辺と平行、あるいは多角形の頂点上にある場合は誤判定してしまうのでそれも考慮しないとなりません)
非常にシンプルなアルゴリズムですね。
ただ、自己交差をしている多角形の場合は正常に判定できないようです。
※ 自己交差とは、辺がどこかで交差してしまっていることを指します。
Winding Number Algorithm
もうひとつのアルゴリズムは「Winding Number Algorithm」です。
こちらは、調査点から見て、多角形の各頂点をぐるっと周回して得られる角度の合計がどうなるかで判定を行うものです。
参考にした記事から引用させていただくと以下のように説明されています。
Winding Number Algorithmは、点Pを中心に多角形Tの辺を順番になぞっていった時に点Pの周りを何回回転するかを計算し、その数(
)によって内側・外側の判定を行います。
この時、であれば多角形Tは点Pを取り囲んでいることになるので、点Pは多角形Tの内側にいると判定します。逆に、点Pが多角形Tの外側にいると判定されるのは
の時だけです。
※ 余談ですが、「Winding」には「巻き取る」とか「うねり」という意味があるようです。
そして今回実装したのはこちらのアルゴリズムです。
なお、こちらのアルゴリズム、「角度」の算出にが出てくるため、調査対象の点や多角形の頂点数が多くなると処理負荷が高まります。
参考にした記事では、最初の「Crossing Number Algorithm」を少し拡張したような別の方法での実装方法も紹介されていました。
以下では、Unityで両方実装したので双方について、Unityでの実装をベースに解説したいと思います。
角度を利用したアルゴリズムの実装解説
「とある点」が凹多角形の内側にあるのか外側にあるのかの判断はとてもシンプルです。
「とある点」と凹多角形の各頂点との成す角の合計が0かそれ以外か、で判定することができます。
※ なお、ここでの角については時計回りを正、反時計回りを負としています。つまり符号付き角度で考えることが重要です。(参考にした記事では反時計回りを正としていましたが、ここは多分、決めの問題です。今回のサンプルでは時計回りを正として実装しました)
まずはシンプルに三角形について考えてみましょう。(凹多角形ではないですが、イメージを掴みやすくするために単体で考えます)
以下のように、三角形の内側に点がある場合、それぞれの頂点と「とある点」とで辺を作り、その成す角(偏角)について考えてみます。
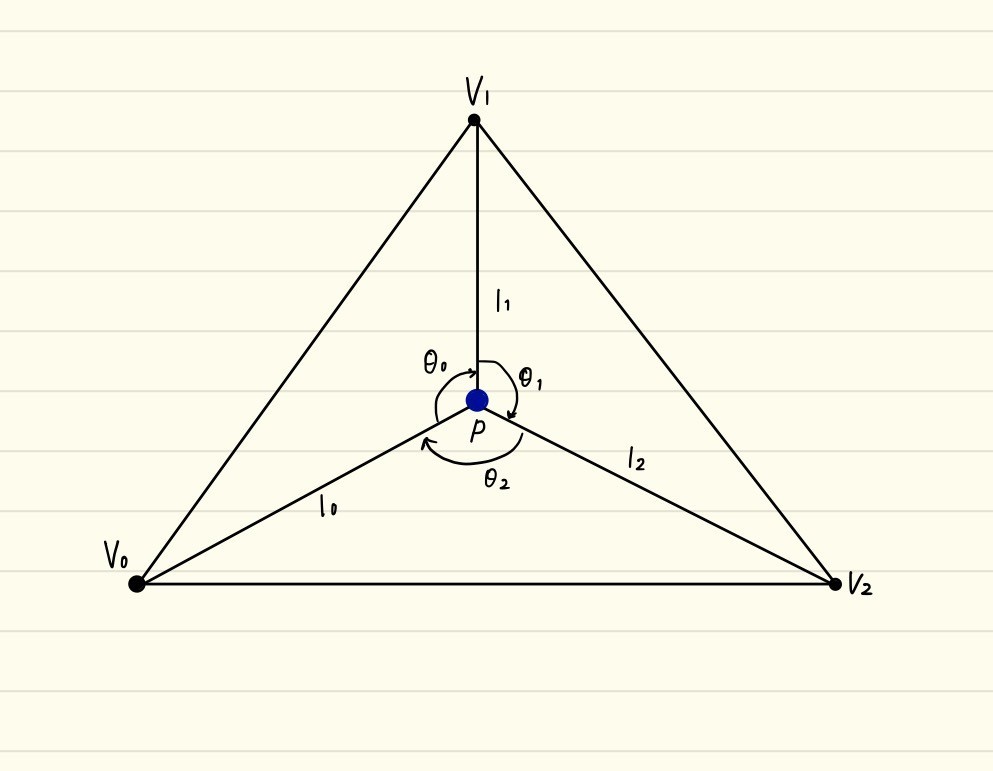
を合計すると360度になるのが分かります。
角の作り方は点と凹多角形の各頂点とを結び辺を作ります。
頂点を()としたとき、点
とで作る辺を(
)とします。
偏角は
とが成す角となります。そしてそれを合計するので、
さらに、1周は360度(=)なので、
で割ることで「何周したか」を計算することができます。まとめると、
と表すことが出来ます。
さて、同様にして四角形でもやってみましょう。
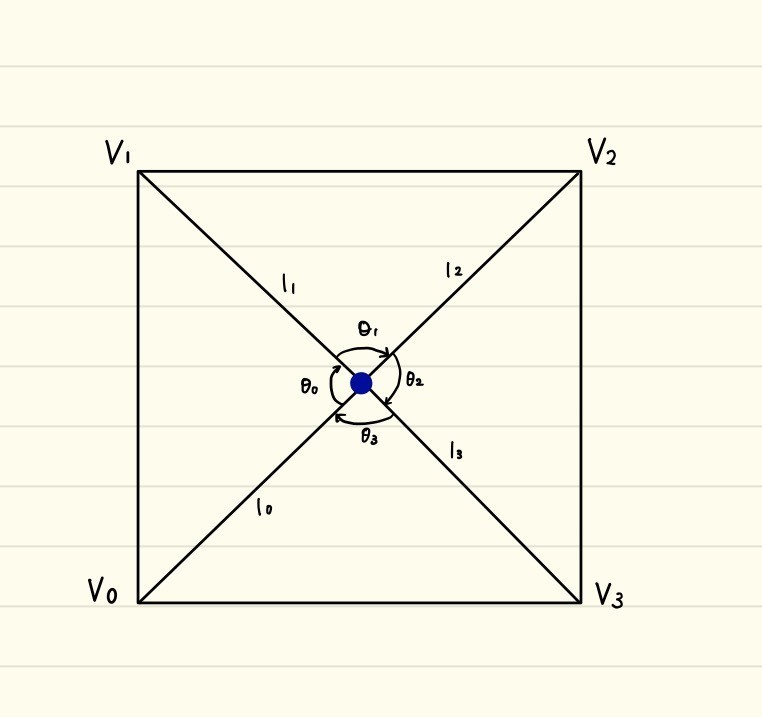
確かに四角形でも360度になることが分かります。
では今度は「とある点」を外側に出して同様の計算をしてみましょう。
すると、以下の図のようにきれいに角度の合計が0にるのが分かるかと思います。
(矢印の向きが違うのは符号付き角度を表しています)
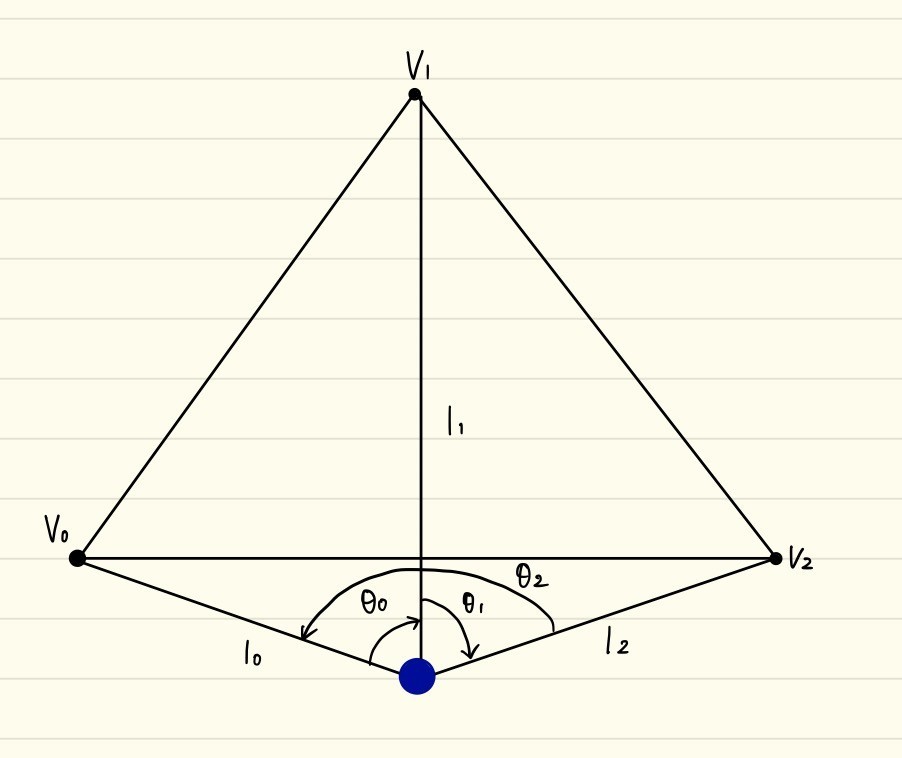
この事実を利用して、凹多角形の外側に点がある場合は偏角の合計が0の場合は外、それ以外の場合は内側、として判断します。
ちなみに、参考にした記事では辺が交差している、より複雑な形状についても判定しています。
その場合でも、外側の場合は0、そしてそれ以外の場合は1以上になることもあるようです。
角度を使ったアルゴリズムのソースコード
上記の内容を実際にC#で実装したコードが以下になります。
////// 多角形を構成する頂点リストと対象点とを使って、対象点が多角形内に含まれるかをテストする /// static public class PointInArea { private const float _unit = 1f / 360f; ////// 調査点が多角形の内外どちらにあるかを判定する /// /// 多角形を構成する頂点リスト /// 調査点 /// 多角形が存在する平面の法線 ///調査点が内側にある場合はtrue static public bool _Check(Vector3[] positions, Vector3 target, Vector3 normal) { float result = 0; for (int i = 0; i < positions.Length; i++) { Vector3 l1 = positions[i] - target; Vector3 l2 = positions[(i + 1) % positions.Length] - target; float angle = Vector3.Angle(l1, l2); Vector3 cross = Vector3.Cross(l1, l2); if (Vector3.Dot(cross, normal) < 0) { angle *= -1; } result += angle; } result *= _unit; // 時計回り・反時計回りどちらもありえるため絶対値で判定する return Mathf.Abs(result) >= 0.01f; } }
コードの行数もそれほど多くなく、とてもシンプルに判定できているのが分かるかと思います。
メソッドの第一引数のpositionsが多角形を構成する頂点配列、targetが調査点P、normalは多角形が存在する平面の法線です。
平面法線を使って回転の方向を判定
法線について少しだけ補足します。
法線を必要としているのは、「偏角の向き」を判断するためです。
2辺の角度を求めるには内積を用いて計算するか、UnityであればVector3.Angleによって角度を求めることができます。
しかしその角度は符号がついていません。つまり、「どちら周りか」が分からないのです。
そこで、平面の法線を利用して外積を求めることでどちら周りの角度なのかを判断しているというわけです。
今回の実装では、選択したふたつの辺の外積と面の法線との外積がマイナス方向だった場合は逆回転として扱うようにしています。
浮動小数点誤差などを考慮
そして最後に、計算結果が0より上かを判定基準としています。
が、ここでも少しだけ細かい処理が入っています。
まず、すべてが逆回転の場合、resultの角度はマイナスになります。
が、それは見る角度が反対だっただけで、内外の判定には関係ありません。
なので絶対値を使って判定するためにMathf.Absを使っています。
最後の比較部分ですが、本来なら0であるかどうか、で判定を行いますが浮動少数点の計算誤差によりきれいに0になりません。
そこで、ある程度0に近い値を利用して、それ以上であれば内側、という判定にしています。
角度を利用したアルゴリズムについては以上です。
次は計算コストを軽量化したアルゴリズムでの実装を解説します。
辺との交差を利用したアルゴリズムの実装解説
こちらはまだしっかりと理解しているわけではないですが、参考にした記事から引用させていただくと以下のようになります。
Crossing Number Algorithmと同様に点Pから伸びる水平線
と多角形Tの辺
が交差する数をカウントし、交差する辺が上向きであるか下向きで加算するか減算するかを変えるということです。 つまり、
- 上向きの辺と水平線Rが交差する場合は
を+1
- 下向きの辺と水平線Rが交差する場合は
を-1
とします。 こうすることで、Crossing Number Algorithmに
- ルール5. 上向きの辺と交差する場合、
を+1する。
- ルール6. 下向きの辺と交差する場合、
を-1する。
Crossing Number Algorithmに、方向を持った辺との交差をルールに加えることによってを求めることができる、ということのようです。
まずはソースコードを見たほうが早いと思うので見てみましょう。
辺との交差を用いたアルゴリズムのソースコード
////// 多角形を構成する頂点リストと対象点とを使って、対象点が多角形内に含まれるかをテストする /// static public class PointInArea { ////// 調査点が多角形の内外どちらにあるかを判定する /// /// 多角形を構成する頂点リスト /// 調査点 /// 多角形が存在する平面の法線 ///調査点が内側にある場合はtrue static public bool Check(Vector3[] points, Vector3 target, Vector3 normal) { // XY平面上に写像した状態で計算を行う Quaternion rot = Quaternion.FromToRotation(normal, -Vector3.forward); Vector3[] rotPoints = new Vector3[points.Length]; for (int i = 0; i < rotPoints.Length; i++) { rotPoints[i] = rot * points[i]; } target = rot * target; int wn = 0; float vt = 0; for (int i = 0; i < rotPoints.Length; i++) { // 上向きの辺、下向きの辺によって処理を分ける int cur = i; int next = (i + 1) % rotPoints.Length; // 上向きの辺。点PがY軸方向について、始点と終点の間にある。(ただし、終点は含まない) if ((rotPoints[cur].y <= target.y) && (rotPoints[next].y > target.y)) { // 辺は点Pよりも右側にある。ただし重ならない // 辺が点Pと同じ高さになる位置を特定し、その時のXの値と点PのXの値を比較する vt = (target.y - rotPoints[cur].y) / (rotPoints[next].y - rotPoints[cur].y); if (target.x < (rotPoints[cur].x + (vt * (rotPoints[next].x - rotPoints[cur].x)))) { // 上向きの辺と交差した場合は+1 wn++; } } else if ((rotPoints[cur].y > target.y) && (rotPoints[next].y <= target.y)) { // 辺は点Pよりも右側にある。ただし重ならない // 辺が点Pと同じ高さになる位置を特定し、その時のXの値と点PのXの値を比較する vt = (target.y - rotPoints[cur].y) / (rotPoints[next].y - rotPoints[cur].y); if (target.x < (rotPoints[cur].x + (vt * (rotPoints[next].x - rotPoints[cur].x)))) { // 下向きの辺と交差した場合は-1 wn--; } } } return wn != 0; } }
冒頭ではまず、平面の計算を行いやすくする目的でXY平面へ全頂点を写像したのちに計算を行っています。
それ以後の実装に関しては冒頭の記事を参考にさせていただきました。
最後の点の評価部分については図解してみました。
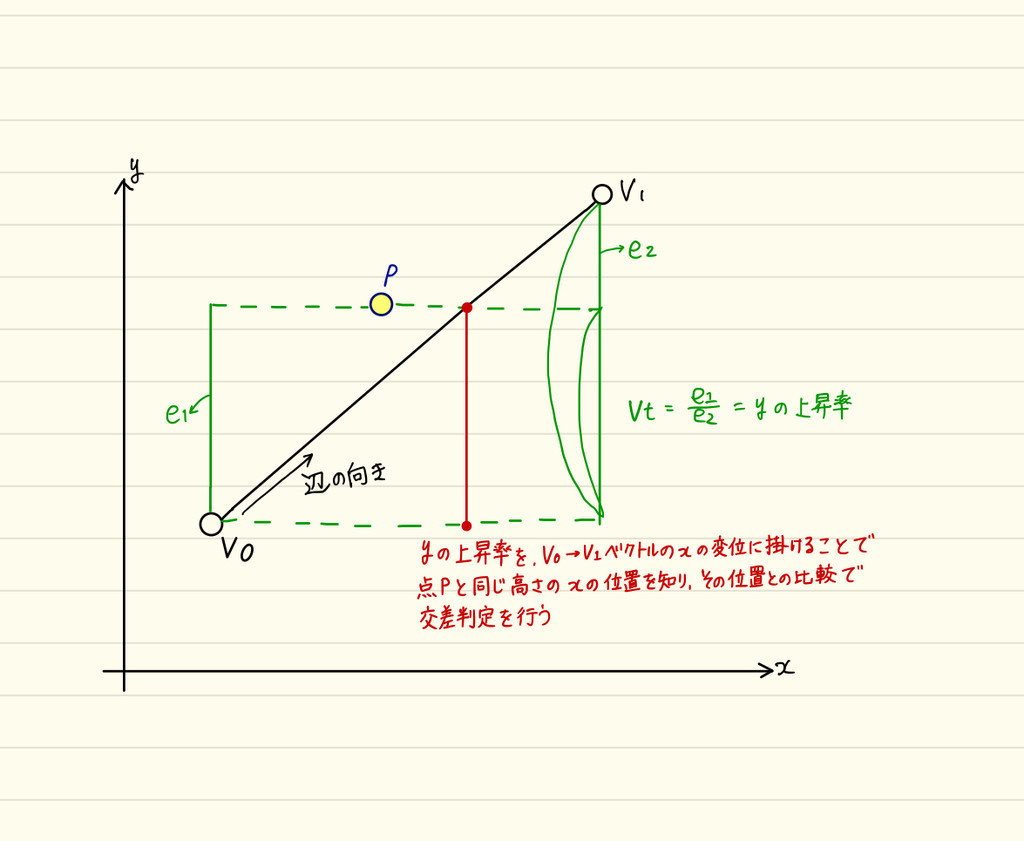
から
が辺の方向ベクトルとなります。
そしてvtは辺ベクトルのy値の上昇率です。
それをxにも適用することで、点と同じ高さの辺の
x位置を知り、それとの比較によって交差判定を行っています。
上の図で言うと、中央付近の赤いラインが該当位置のxの位置を示しています。
この赤いラインと辺ベクトルとの交点が、点と同じ高さの辺上の
x位置となります。
これと比較して、点より右側にあれば交差している、というわけです。
こちらのアルゴリズムでは角度は登場せず、辺との交差回数を増減することによって「何周したか」を判定していることになります。
前述の角度を求めるアルゴリズムと比べて、実際に計測してみたらだいぶ計算負荷に差があったので、基本的には下の実装を利用するのが良さそうです。
ただ、アルゴリズム自体の理解は前述のものを最適化したものなので前者をしっかり把握することが大事だと思います。