シャボン玉風シェーダを実装してみたのでメモ

さて、BRDFは光の反射をモデル化したものと書きましたが、現在のレンダリング方程式ではすべての物質の光の反射を扱えるほど精巧には出来ていません。ある一定の条件でのみ成り立つものだったり、特定の表現のための関数などもあります。それを匠に使いこなしながら、今日のフォトリアリスティックな映像は作られているというわけですね。

そして今回の論文ではそのBRDF的な関数を提案するものではありません。

複雑な関数から導き出すのではなくテクスチャに情報を格納し、そこから構造色（詳細は後述）を決定しよう、というものです。

構造色とは

論文の説明から引用させてもらうと、

構造色は微細構造がもたらす光学現象による発色であるため、視点位置や照明環境に応じて色が変化するという特徴がある。

シャボン玉やCDの記録面を見ると分かると思いますが、見る角度や照明の状態に応じて色が変化しますよね。ああいう、視点や光源によって変化する色を「構造色」と言うようです。

構造色の仕組み

構造色は前述のように、視点と光源位置によって見え方が変わるものです。ではなぜ、視点や光源位置に応じて色が変化するのでしょうか。

論文から画像を引用させてもらうと以下のような構造になっているものが「構造色」を表します。

膜やスリットなどに光が入り、入射した光と反射した光の「光路」に差が生じると、別の反射光と干渉を起こして色が変化する、というのが理由のようです。（光は波の性質も持っているのでこうした干渉が起こる）

光の反射

反射光の話が出ました。これはまさに、前述のBRDFの話と同じですね。
3DCGでは光の反射をどう扱うかで色が決まります。

そして今、入射光と反射光について以下のように定義します。

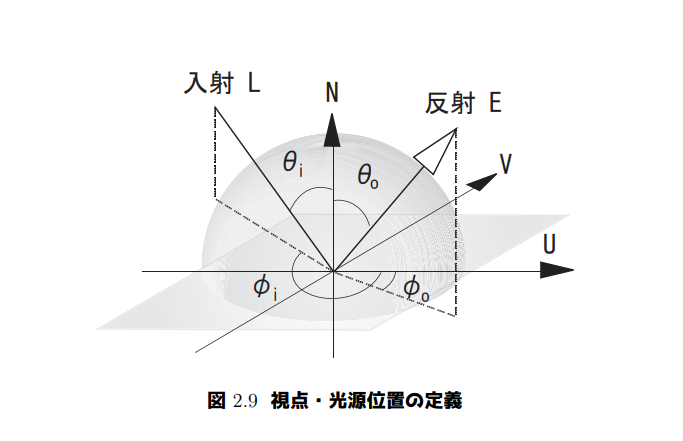
上図は論文から引用したものです。
これは、注目している点の光の入射・反射を $\theta$ と $\phi$ によって表した図です。
入射光の $\theta$ と $\phi$ 、そして反射光の $\theta$ と $\phi$ の4つのパラメータがあります。

この4パラメータが大事になります。

構造色を決定する

さて、大まかに概観したところで実際に構造色を決定する部分を見ていきましょう。
前述のように、入射・反射の角度の4パラメータが大事なポイントです。

また論文から画像を引用させていただくと構造色を決定するフローは以下のようになります。

視点位置 $E$ 、光源位置 $L$ 、それによって決定する $(\theta_i, \phi_i)$ , $(\theta_o, \phi_o)$ の4パラメータ、そしてUV値がどのように使われるかを示した図です。

続いて以下の図を見てください。

パラメータをどう扱うかを図示したものです。

詳細を説明する前にさらに次の図を見てください。

こちらは実際にレンダリングに使用するテクスチャです。
左上がシャボン玉の厚みテクスチャで、UV値を利用して単純にアクセスされるテクスチャです。

次に右上が光路差を格納したテクスチャで、視点・光源の角度によってアクセスされるテクスチャです。

そして下の最後のものが構造色テクスチャです。
最終的に色としてマッピングされるのはこの構造色テクスチャです。

つまり、下部の構造色テクスチャのどの位置をフェッチしたらいいか、を光路差情報を元に決定するのが実装概要となります。

構造色テクスチャのフェッチ位置を計算

さてではどのようにしてフェッチ位置を決定するのか。それが、ふたつ前に載せた画像です。再掲すると以下の画像です。

左の図は通常のUV値を利用して「厚みテクスチャ」にアクセスする様子を描いています。
場所依存の「厚み」を表現しているわけですね。ある意味で法線マップと同様のことをやっています。なのでここは細かい説明は不要でしょう。

右側のテクスチャが今回の肝である「光路差テクスチャ」です。
前述した3枚のテクスチャのうち、「視点・光源依存テクスチャ」と書かれているテクスチャがそれです。

そしてこのテクスチャから値を取得するわけですが、「どこの値を取り出すのか」を決定するのが、前段で大事だと話した4つのパラメータ、つまり $(\theta_i, \phi_i)$ , $(\theta_o, \phi_o)$ です。

論文では以下のように説明されています。

視点・光源依存テクスチャは、視点および光源位置による光路差の変化を表現するテクスチャである。テクスチャは図3.3の座標軸をもち、横軸に法線成分、縦軸に接線成分が対応している。ただしTは接線ベクトルであり、テクスチャ座標のUの方向を持つ単位ベクトルである。左半分が光源位置による光路差であり、光源 $L$ により $L \cdot N$ および $L \cdot T$ が決まる。同様に右半分が視点位置による光路差であり、視点 $E$ により $E \cdot N$ および $E \cdot T$ が決まる。よってテクスチャの中心がオブジェクトの面に垂直な位置、つまり法線上に視点・光源がある場合に対応する。

特に、

テクスチャの中心がオブジェクトの面に垂直な位置、つまり法線上に視点・光源がある場合に対応する。

を見ると、テクスチャの中心が視点・光源がともに法線上にある場合に対応することになります。

計算してみましょう。法線上ということは（ $L \cdot N = 1$ 、 $L \cdot T = 0$ ）同様に（ $E \cdot N = 1$ 、 $E \cdot T = 0$ ）となります。
この値が、視点・光源依存テクスチャのどこにあるかを見てみると確かにテクスチャの中心にマッピングされますね。

さて、ではこの事実をどう利用するのでしょうか。考え方はこうです。
視点・光源依存テクスチャは0 ~ 1の正規化された値が格納されています。値はただのfloatですね。なのでスカラーです。しかしテクスチャから色をフェッチするためにはUV、つまりfloat2のベクトルとしての値が必要です。

つまり、入射光の $(\theta_i, \phi_i)$ のふたつのパラメータによってひとつのスカラーが得られます。同様に反射光の $(\theta_o, \phi_o)$ のふたつのパラメータによってひとつのスカラーが得られます。

このふたつのスカラーを利用すればUVとしてのベクトルを得ることができますね。

論文の別の画像を引用させてもらうと以下のように説明されています。

つまり入射光の角度から算出されたスカラーをU軸に、反射光の角度から算出されたスカラーをV軸に割り当てることで構造色が決定できる、というわけですね。

そしてそれを実際に実行した結果がこちら↓

値を計算しているところのコードを抜粋すると以下になります。

float d = /* Calculate thickness */

float u, v;

// Calculate U.
{
    float ln = dot(i.lightDir, i.normal);
    ln = (ln * 0.5) * d;

    float lt = dot(i.lightDir, i.tangent);
    lt = ((lt + 1.0) * 0.5) * d;

    u = tex2D(_LETex, float2(ln, lt)).x;
}

// Calculate V.
{
    float en = dot(i.viewDir, i.normal);
    en = ((1.0 - en) * 0.5 + 0.5) * d;

    float et = dot(i.viewDir, i.tangent);
    et = ((et + 1.0) * 0.5) * d;

    v = tex2D(_LETex, float2(en, et)).x;
}

Uの値は入射光（i.lightDir）によって計算され、Vの値は反射光（i.viewDir）によって計算されていますね。
ここで求まったUVの値を使って構造色テクスチャから色をフェッチしてあげれば晴れて、視点・光源に依存した色、つまり構造色を決定することができる、というわけです。

最後に

構造色の計算については以上です。
今回はそれ以外にもシンプルなPhong反射とリムライティングを追加しています。なので全部が正確なレンダリング、というわけではないですがそれなりに説得力のある絵になったかなと思います。

コード全体は長くないので全文を掲載しておきます。実際に動作するものを見たい場合はGitHubからダウンロードしてご覧ください。

Shader "Unlit/Bubble"
{
    Properties
    {
        [PowerSlider(0.1)] _F0("F0", Range(0, 1)) = 0.02
        _RimLightIntensity ("RimLight Intensity", Float) = 1.0
        _Color ("Color", Color) = (1, 1, 1, 1)
        _MainTex ("Texture", 2D) = "white" {}
        _DTex ("D Texture", 2D) = "gray" {}
        _LETex ("LE Texture", 2D) = "gray" {}
        _CubeMap ("Cube Map", Cube) = "white" {}
    }

    SubShader
    {
        Tags
        {
            "RenderType"="Transparent"
            "Queue"="Transparent"
        }
        LOD 100

        Pass
        {
            Blend SrcAlpha OneMinusSrcAlpha

            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"
            #include "./PerlinNoise.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float3 normal : NORMAL;
                float3 tangent : TANGENT;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
                float3 normal : TEXCOORD1;
                float3 tangent : TEXCOORD2;
                float3 viewDir : TEXCOORD3;
                float3 lightDir : TEXCOORD4;
                half fresnel : TEXCOORD5;
                half3 reflDir : TEXCOORD6;
            };

            sampler2D _MainTex;
            sampler2D _DTex;
            sampler2D _LETex;

            UNITY_DECLARE_TEXCUBE(_CubeMap);

            float _F0;
            float _RimLightIntensity;
            float4 _MainTex_ST;
            fixed4 _Color;

            v2f vert (appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                o.normal = v.normal;
                o.tangent = v.tangent;
                o.viewDir  = normalize(ObjSpaceViewDir(v.vertex));
                o.lightDir = normalize(ObjSpaceLightDir(v.vertex));
                float3 halfDir = normalize(o.viewDir + o.lightDir);
                o.fresnel = _F0 + (1.0h - _F0) * pow(1.0h - dot(o.viewDir, halfDir), 5.0);
                o.reflDir = mul(unity_ObjectToWorld, reflect(-o.viewDir, v.normal.xyz));
                return o;
            }

            fixed4 frag(v2f i) : SV_Target
            {
                i.uv = pow((i.uv * 2.0) - 1.0, 2.0);
                //float d = tex2D(_DTex, i.uv + _Time.xy * 0.1);
                float d = perlinNoise((i.uv + _Time.xy * 0.1) * 3.0);

                float u, v;

                // Calculate U.
                {
                    float ln = dot(i.lightDir, i.normal);
                    ln = (ln * 0.5) * d;

                    float lt = dot(i.lightDir, i.tangent);
                    lt = ((lt + 1.0) * 0.5) * d;

                    u = tex2D(_LETex, float2(ln, lt)).x;
                }

                // Calculate V.
                {
                    float en = dot(i.viewDir, i.normal);
                    en = ((1.0 - en) * 0.5 + 0.5) * d;

                    float et = dot(i.viewDir, i.tangent);
                    et = ((et + 1.0) * 0.5) * d;

                    v = tex2D(_LETex, float2(en, et)).x;
                }

                float2 uv = float2(u, v);
                float4 col = tex2D(_MainTex, uv);

                float NdotL = dot(i.normal, i.lightDir);
                float3 localRefDir = -i.lightDir + (2.0 * i.normal * NdotL);
                float spec = pow(max(0, dot(i.viewDir, localRefDir)), 10.0);

                float rimlight = 1.0 - dot(i.normal, i.viewDir);

                fixed4 cubemap = UNITY_SAMPLE_TEXCUBE(_CubeMap, i.reflDir);
                cubemap.a = i.fresnel;

                col *= cubemap;
                col += rimlight * _RimLightIntensity;
                col += spec;

                return col;
            }
            ENDCG
        }
    }
}