e.blog

主にUnity/UE周りのことについてまとめていきます

Unityで流体シミュレーションを実装する 〜 実装編 〜

C# シェーダ アニメーション Unity ComputeShader パーティクル

概要

前回は流体シミュレーションの概念編を書きました。

edom18.hateblo.jp

今回は前回説明した内容を元に実際に実装したプログラムに関して解説していきたいと思います。
ちなみに実行したデモ動画はこちら↓

また今回実装したものはGitHubにアップしてあります。

github.com

おさらい

まずは簡単におさらいから始めましょう。
流体シミュレーションはナビエ・ストークス方程式というのを解くことで実現するのでした。

ナビエ・ストークス方程式は以下の形をした方程式です。

f:id:edo_m18:20200211103647j:plain

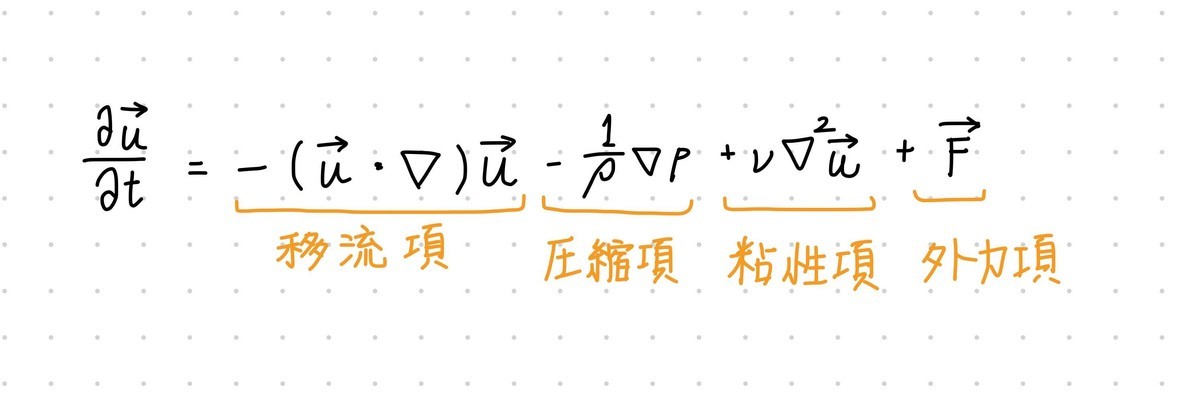
実装ではまさにこの右辺を求めたいわけです。毎フレーム、パーティクルがどう動くのかが知りたいわけなので。
つまりプログラムで達成すべきは、各ピクセルに保存された速度を更新して次にパーティクルをどう動かすべきかを計算することです。

今回はその計算にCompute Shaderを利用しました。

Compute Shaderについては過去に2つほど記事を書いているので使い方については以下の記事を参照ください。今回は使い方に関しては割愛します。

edom18.hateblo.jp

edom18.hateblo.jp

実装のフロー

さて、まずはどう実装するかのフローを確認しておきましょう。

なお、本実装にあたり以下の「Nikkei Development Book」を大いに参考にさせていただきました。ありがとうございます。

note.com

実装についてはCompute Shaderを用いて以下のステップで各ピクセルを更新していきます。

  1. 前フレームの速度を用いて移流を計算
  2. マウスによる外力を計算
  3. (1), (2)によって計算された速度を元に発散を計算
  4. (3)の発散を元に圧力を計算
  5. (4)の圧力を元に速度を調整
  6. 求まった速度を利用してピクセルの色を更新

という流れになります。
ナビエ・ストークス方程式で言うと(1)が移流項、(2)が外力項、(3)と(4)が圧力項となります。

前回の概念編では書きましたが、今回は粘性項は考慮していません。毎フレーム0.99などを掛けて徐々に減速されるようになっています。

実際の実装

ここからは実際の実装を元に解説していきたいと思います。

実装自体はそれほど複雑ではなく、実際に実装したCompute Shaderのソースコードはそこまで長くありません。（ソースコードはこちら）
見てもらうと分かりますが140行足らずしかありません。（C#などプロジェクト全体はGitHubを参考にしてください）

カーネルの定義

定義されているカーネルは以下。

#pragma kernel UpdateAdvection
#pragma kernel InteractionForce
#pragma kernel UpdateDivergence
#pragma kernel UpdatePressure
#pragma kernel UpdateVelocity
#pragma kernel UpdateTexture

実装フロー分のカーネルが定義されているのが分かるかと思います。

上から順に、

  • 移流の計算
  • 外力の計算
  • 発散の計算
  • 圧力の計算
  • 速度の計算
  • ピクセル位置の計算

となっています。

念の為カーネルについて補足しておくと、Compute Shaderの「核」となる関数で、C#から呼び出す（Dispatch）ことができる関数です。つまりこれらカーネルを利用してテクスチャを更新していく、というわけですね。

テクセルへのアクセス

テクセルとはテクスチャのピクセルの意味です。 Wikipediaから引用すると、

テクセル（英: texel）は、コンピュータグラフィックスで使用するテクスチャ空間の基本単位である。

と記載されています。

実装の詳細に入る前に各計算で共通している部分について先に説明しておきます。
具体的には以下の部分です。

float w = _Width;
float h = _Height;

float3 px = float3(1.0/w, 1.0/h, 0.0);
float2 uv = float2(id.x / w, id.y / h) + px.xy * 0.5;

テクセルの基本単位の計算

_Widthと_Heightはuniform変数としてC#から渡された値です。つまりはテクスチャのサイズです。

そして最後の2行が、「1テクセル分の幅（基本単位）」と「サンプリングするUV値」を計算によって求めています。

シェーダでは大体の場合において値を0.0 ~ 1.0で扱います。そのため1.0を幅および高さで割ることで1テクセル分の幅を求めることができます。

例えば128 x 128のテクスチャの場合、1.0 / 128 = 0.0078125という値が1テクセル分の幅ということになります。

UVの計算

そして最後のUVの計算ですが、（前知識として）カーネルでは計算しているスレッドのIDをuint型の値で受け取ることができます。例えば以下のように受け取ります。

void UpdateTexture(uint2 id : SV_DispatchThreadID) { ... }

上の例ではuint2型で受け取っているので、つまりはテクスチャのxとyの2次元配列の添字として利用することができるわけです。（Compute Shaderのこのあたりの細かい内容については以前のスレッド編の記事をご覧ください）

なので普通にテクスチャのテクセルにアクセスするだけなら以下のように指定することができます。

// uint2なのでそのまま指定すれば該当する位置のテクセルが取得できる
float4 col = texture[id];

しかし今回の例では以下のように計算してUV値を求めています。

float2 uv = float2(id.x / w, id.y / h) + px.xy * 0.5;

idを幅と高さで割ることで対象とするUVの位置の左下の値が計算できます。

ここであえて左下と書いたのにはわけがあります。

どういうことかと言うと、テクスチャ空間では実はピクセルの単位ごとにアクセスするのではなくさらに細かい位置までアクセスすることが可能となっています。

データとしてはピクセル単位で保存されているわけですが、その間の値を指定した場合はその間の値を補間した値が返されます。

この補間はフィルタと呼ばれ、バイリニアフィルタなどは聞いたことがある人もいるかと思います。
このあたりの内容については以下の記事を参照ください。

karanokan.info

このことから、1ピクセルの中だけを見ても細かな位置に意味があることが分かります。
そのために「左下」と書いたわけです。

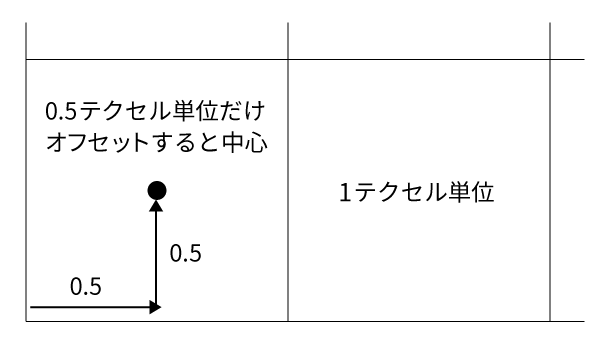
ピクセルの中心にアクセスするためにオフセットさせる

計算ではさらに続けてpx.xy * 0.5を足しています。これは「基本単位の半分だけオフセットさせる」という意味になります。

前述の通り、オフセット前の値はテクセルの「左下」の値でした。
そしてテクセル単位の半分だけオフセットさせれば無事、テクセルの中心へのアクセスとなります。

そしてそれを加味した状態でのテクセルへのアクセスは以下のようになります。

f:id:edo_m18:20200223100124p:plain

全体で利用しているSwapBufferについて

これから説明していく中で「バッファ」という言葉を使いますが、実態はRenderTexureです。
今回の実装ではこれをラップするSwapBufferというクラスを実装しました。

これは単純にふたつのRenderTextureを内部に保持し、内容を更新する際に交換（スワップ）して簡単にCompute Shaderへテクスチャを渡すことができるようにした便利クラスです。

実装は以下のようにシンプルになっています。

public class SwapBuffer
{
    private RenderTexture[] _buffers = new RenderTexture[2];

    public RenderTexture Current => _buffers[0];
    public RenderTexture Other => _buffers[1];

    private int _width = 0;
    private int _height = 0;

    public int Width => _width;
    public int Height => _height;

    public SwapBuffer(int width, int height)
    {
        _width = width;
        _height = height;

        for (int i = 0; i < _buffers.Length; i++)
        {
            _buffers[i] = new RenderTexture(width, height, 0, RenderTextureFormat.ARGBHalf, RenderTextureReadWrite.Linear);
            _buffers[i].enableRandomWrite = true;
            _buffers[i].Create();
        }
    }

    public void Swap()
    {
        RenderTexture temp = _buffers[0];
        _buffers[0] = _buffers[1];
        _buffers[1] = temp;
    }

    public void Release()
    {
        foreach (var buf in _buffers)
        {
            buf.Release();
        }
    }
}

内部にRenderTextureをふたつ保持し、スワップを簡単に行えるようにするのと、Currentとそれ以外を指定して簡単にアクセスできるようにするだけのシンプルなものです。

移流項の計算

まずは移流項から見ていきましょう。移流項はとてもシンプルです。
移流項の計算は以下になります。

[numthreads(8,8,1)]
void UpdateAdvection(uint2 id : SV_DispatchThreadID)
{
    float w = _Width;
    float h = _Height;

    float3 px = float3(1.0/w, 1.0/h, 0.0);
    float2 uv = float2(id.x / w, id.y / h) + px.xy * 0.5;

    float2 velocity = _UpdateVelocity.SampleLevel(_LinearClamp, uv, 0).xy;
    float2 result = _SourceVelocity.SampleLevel(_LinearClamp, uv - velocity * _DeltaTime, 0).xy;

    _ResultVelocity[id] = float4(result, 0.0, 1.0);
}

ここでやっていることは移流、つまり流体が流れてきた際の速度の変化を計算しています。
上記コードではふたつの速度テクスチャを利用して計算を行っています。

C#側の呼び出しも合わせて見てみましょう。

private void UpdateAdvection()
{
    _shader.SetTexture(_kernelDef.UpdateAdvectionID, _propertyDef.SourceVelocityID, _velocityBuffer.Current);
    _shader.SetTexture(_kernelDef.UpdateAdvectionID, _propertyDef.UpdateVelocityID, _velocityBuffer.Current);
    _shader.SetTexture(_kernelDef.UpdateAdvectionID, _propertyDef.ResultVelocityID, _velocityBuffer.Other);

    _shader.Dispatch(_kernelDef.UpdateAdvectionID, _velocityBuffer.Width / 8, _velocityBuffer.Height / 8, 1);

    _velocityBuffer.Swap();
}

Source VelocityとUpdate Velocityは同じバッファを指定しています。
Result Velocityは結果を保持するため別のバッファを渡しています。

イメージ的には、現在の速度場の各ピクセルの速度を利用して次のフレームのための速度に更新する、ということをやっています。

現在の速度場テクスチャの値を取得しそれをvelocityとし、そのマイナス方向のテクセルの値を自身の値とする、という計算を行っています。

テクセルのフェッチ位置の計算は以下の部分ですね。

uv - velocity * _DeltaTime

現在のテクセルの位置に速度を上乗せして、その位置のテクセルをフェッチしているということです。
また取得したのが速度なので_DeltaTimeを掛けて単位を秒単位にしてから計算している点に注意が必要です。

外力の計算

次は外力の計算です。
外力は（今回は）マウスの動きを利用しています。
もちろんマウス以外から外力を受けるようにしても問題ありません。

要はこの項は流体がなにによってどう動かされているかを計算します。
なので一定時間外力を加えたあとに外力を計算しなくしても（常にゼロにしても）、流体自体に残されている速度によって徐々に拡散が起こります。（ただ速度の拡散によって徐々に動きが穏やかになっていきます。無風のときの湖面が鏡のようになっているようなイメージですね）

[numthreads(8,8,1)]
void InteractionForce(uint2 id : SV_DispatchThreadID)
{
    float w = _Width;
    float h = _Height;

    float2 px = float2(1.0 / w, 1.0 / h);
    float2 uv = float2(id.x / w, id.y / h) + px.xy * 0.5;

    float3 vec = _SourceVelocity.SampleLevel(_LinearClamp, uv, 0).xyz;

    float dist = distance(_Cursor * px * _Scale, uv);

    if (dist < 0.005)
    {
        vec.xy += _Velocity.xy * px;
    }

    _ResultVelocity[id] = float4(vec, 1.0);
}

計算に利用している_Cursorはマウスの位置です。これとpxを乗算することで正規化されたテクスチャの位置を知ることができます。（_Scaleは単にサイズ調整のためのものです）

そしてその値と現在のUV位置との距離を測ることで、マウスの影響下にあるテクセルなのかどうかを判断しています。
その閾値として0.005をハードコードしていますが、この値を大きくすると影響を受ける範囲が大きくなります。

あとは、マウスの影響範囲だと判断された場合に、C#側から渡されたマウス速度（_Velocity）を加算することで速度を更新しています。

注意点としてはpxを掛けてテクスチャ空間での単位に変換してやる必要があります。
これは、C#側で計算された速度がスクリーン座標系のため値が数十〜数百という値になっており、これをそのまま利用するととんでもない速度になってしまうためです。

発散の計算

続いて発散の計算です。
この前の段階までで、前フレームから今フレームの移流の計算、およびマウス操作による外力が加わり、速度場が変化した状態になっています。

ただ、このままだと流体としての振る舞いにはならないため、流体らしく動くよう全体の速度を調整する必要があります。

そのための項が圧力項なのですが、全体の圧力を求めるためにこの「発散」の値が必要になります。

ということで次は発散を求めていきます。

[numthreads(8,8,1)]
void UpdateDivergence(uint2 id : SV_DispatchThreadID)
{
    float w = _Width;
    float h = _Height;

    float3 px = float3(1.0 / w, 1.0 / h, 0);
    float2 uv = float2(id.x / w, id.y / h) + px.xy * 0.5;

    float x0 = _SourceVelocity.SampleLevel(_LinearClamp, uv - px.xz, 0).x;
    float x1 = _SourceVelocity.SampleLevel(_LinearClamp, uv + px.xz, 0).x;
    float y0 = _SourceVelocity.SampleLevel(_LinearClamp, uv - px.zy, 0).y;
    float y1 = _SourceVelocity.SampleLevel(_LinearClamp, uv + px.zy, 0).y;

    float divergence = (x1 - x0 + y1 - y0);

    _ResultDivergence[id] = float4(divergence.xx, 0.0, 1.0);
}

ここでなぜ場の発散を求めているのかというと、\(\nabla \cdot v = 0\)（発散がゼロ）を前提としているからです。
非圧縮流体の場合どの地点においても発散がゼロになるように計算をする必要があります。

そのため、次の圧縮項の計算に利用するための発散をここで求めています。

発散の求め方

発散の求め方は以下の記事を参考にしてください。

hooktail.sub.jp

上記記事から引用すると発散は以下のように定義されます。

\begin{eqnarray} div A = \nabla \cdot A \\ = \frac{\partial A_1}{\partial x_1} + \frac{\partial A_2}{\partial x_2} + \frac{\partial A_3}{\partial x_3} \end{eqnarray}

これは3次元による表現なので今回の場合は2次元として考えます。（つまり\(x\)と\(y\)だけについて考えます）

上記式の意味は、それぞれの要素の偏微分の値を足し合わせるという意味です。
それを踏まえてコードを見てみるとまさにそうなっているのが分かるかと思います。

float x0 = _SourceVelocity.SampleLevel(_LinearClamp, uv - px.xz, 0).x;
float x1 = _SourceVelocity.SampleLevel(_LinearClamp, uv + px.xz, 0).x;
float y0 = _SourceVelocity.SampleLevel(_LinearClamp, uv - px.zy, 0).y;
float y1 = _SourceVelocity.SampleLevel(_LinearClamp, uv + px.zy, 0).y;

float divergence = (x1 - x0 + y1 - y0);

上下左右のテクセルを取得してその差分（e.g. x1 - x0）を取っています。これはまさに微分の計算ですね。
そしてxとyをそれぞれ微分したものを足し合わせているので、まさに発散の計算となっているわけです。

圧力の計算

次は圧力の計算です。圧力の計算では「ヤコビ法」と呼ばれる、反復による計算で解（の近似）を求める方法を使います。
そのためこの部分だけはC#側から複数回（今回の実装では20回）呼び出して値を更新しています。

C#側のコードを見ると単純にforループで複数回カーネルを呼び出しています。

private void UpdatePressure()
{
    for (int i = 0; i < _numCalcPressure; i++)
    {
        _shader.SetTexture(_kernelDef.UpdatePressureID, _propertyDef.SourcePressureID, _pressureBuffer.Current);
        _shader.SetTexture(_kernelDef.UpdatePressureID, _propertyDef.ResultPressureID, _pressureBuffer.Other);
        _shader.SetTexture(_kernelDef.UpdatePressureID, _propertyDef.ResultDivergenceID, _divergenceTexture);

        _shader.Dispatch(_kernelDef.UpdatePressureID, _pressureBuffer.Width / 8, _pressureBuffer.Height / 8, 1);

        _pressureBuffer.Swap();
    }
}

また圧力自体の解は「ポアソン方程式」を用いて解いています。
つまり「ポアソン方程式をヤコビ法を用いて解く」というのが今回の実装ということになります。

ポアソン方程式やヤコビ法については前回の概念編の記事を参照ください。

以下がその実装です。
このカーネル関数を複数回呼び出すことで各ピクセルにおける圧力の近似解を得ます。

[numthreads(8,8,1)]
void UpdatePressure(uint2 id : SV_DispatchThreadID)
{
    float w = _Width;
    float h = _Height;

    float3 px = float3(1.0 / w, 1.0 / h, 0);
    float2 uv = float2(id.x / w, id.y / h) + px.xy * 0.5;

    float x0 = _SourcePressure.SampleLevel(_LinearClamp, uv - px.xz, 0).r;
    float x1 = _SourcePressure.SampleLevel(_LinearClamp, uv + px.xz, 0).r;
    float y0 = _SourcePressure.SampleLevel(_LinearClamp, uv - px.zy, 0).r;
    float y1 = _SourcePressure.SampleLevel(_LinearClamp, uv + px.zy, 0).r;

    float d = _ResultDivergence[id].r;
    float relaxed = (x0 + x1 + y0 + y1 - d) * 0.25;

    _ResultPressure[id] = float4(relaxed.xx, 0.0, 1.0);
}

ポアソン方程式は注目している点の圧力は近傍の4点の平均から求めるものです。
そのためすべての要素を足して4で割っていますね。（1/4 = 0.25）

概念編の記事で参考にした記事から引用すると、

電荷が無い場合のPoissonの方程式(Laplaceの方程式)の意味するところは，「ある場所の電位は，近傍の電位の平均値に等しい」と言っているに過ぎないことに気がついただろうか．

というわけです。

ここではさらに、前段で求めたdivergenceの値を引いています。
これは非圧縮流体を過程しているため発散がゼロになるように計算する必要があります。

発散がゼロということは、その分近傍の動きからそのまま圧力を受けることと同義ですよね。そのためその圧力としての発散（divergence）を計算に加えているわけです。

速度の計算

さて、いよいよ最後の計算です。（実際にはレンダリングのためのテクスチャ更新もありますが「流体のための計算」という意味ではここが最後です）

前段までで移流項、圧力項、外力項を求めました。
その値を利用して、実際に次のフレームで流体がどうなるのかを計算していきます。

[numthreads(8,8,1)]
void UpdateVelocity(uint2 id : SV_DispatchThreadID)
{
    float w = _Width;
    float h = _Height;

    float3 px = float3(1.0 / w, 1.0 / h, 0);
    float2 uv = float2(id.x / w, id.y / h) + px.xy * 0.5;

    float x0 = _SourcePressure.SampleLevel(_LinearClamp, uv - px.xz, 0).r;
    float x1 = _SourcePressure.SampleLevel(_LinearClamp, uv + px.xz, 0).r;
    float y0 = _SourcePressure.SampleLevel(_LinearClamp, uv - px.zy, 0).r;
    float y1 = _SourcePressure.SampleLevel(_LinearClamp, uv + px.zy, 0).r;

    float2 v = _SourceVelocity.SampleLevel(_LinearClamp, uv, 0).xy;
    float4 v2 = float4((v - (float2(x1, y1) - float2(x0, y0)) * 0.5), 0.0, 1.0);
    v2 *= _Attenuation;

    _ResultVelocity[id] = v2;
}

速度の計算は以下のように行います。

  • 現在の速度のx成分 += (左の圧力 - 右の圧力) * 0.5
  • 現在の速度のy成分 += (上の圧力 – 下の圧力) * 0.5

これをまとめると(v - (float2(x1, y1) - float2(x0, y0)) * 0.5となるわけですね。

そして今回の実装では「粘性項」を求めていません。
近似的に減衰率を速度に掛けることで調整しています。

ちなみに最後の_Attenuationが「減衰率」です。
これはC#側から渡して自由に変更できるようにしています。

ピクセルの計算

ここは流体としての計算ではなく、流体っぽい動きをするための「表現・描画」のための計算となります。
なのでここの部分を別の計算に置き換えて（例えばパーティクルの動きに転化するなど）利用することも可能です。

[numthreads(8,8,1)]
void UpdateTexture(uint2 id : SV_DispatchThreadID)
{
    float w = _Width;
    float h = _Height;

    float3 px = float3(1.0 / w, 1.0 / h, 0);
    float2 uv = float2(id.x / w, id.y / h) + px.xy * 0.5;

    float2 vel = _SourceVelocity.SampleLevel(_LinearClamp, uv, 0).xy;

    float4 col = _SourceTexture.SampleLevel(_LinearClamp, uv - vel * _DeltaTime, 0);

    _ResultTexture[id] = col;
}

計算自体は実は移流の計算と同じです。
つまり、速度テクスチャに保存されている速度を元に、速度分移動した位置のピクセルを持ってきて自身の色とする、ということをやっているわけですね。

移流（つまり速度）では圧力項により徐々に速度が変化していきますが、色はその速度を利用して自身の色を変化させるだけなのでこれだけです。

最後に

最後に完成動画をもう一度。

実はこれを3次元に拡張して煙っぽい動きをするパーティクルの実装として使えないかなーなんて思っています。

おそらくですが、速度テクスチャを3次元に拡張し、それらを速度の影響を与える点として利用してやればいけるのではないかなと。

もしそれっぽく動いたらそれもブログで取り上げます。

ともあれ、かねてから流体表現を実装したいと思っていたことを達成できて感無量です。
とはいえもっと応用しながら理解を深めていきたいと思います。