CustomRenderTextureを使って波紋エフェクトを作る
概要
何番煎じか分かりませんが、CustomRenderTextureを使ってシェーダでお絵かきができると色々表現の幅が増えるので、それの練習のために表題のサンプルを作ってみました。
↓実際に動かしたの動画
CustomRenderTextureでシミュレーションした波形でバンプマップしてみた。 pic.twitter.com/OXhkAitOiD
— edom18@XR / MESON CTO (@edo_m18) 2018年8月22日
サンプルはCustomRenderTextureを使って波動方程式を解き波形を描画、さらにそれをレンダリング用シェーダの法線マップとして入力し、歪みとライティング(ランバート反射とフォン反射)を適用してみたものです。
ダウンロード
今回のサンプルもGithubにアップしてあります。
CustomRenderTextureとは
ドキュメントは以下です。
https://docs.unity3d.com/ja/current/Manual/CustomRenderTextures.htmldocs.unity3d.com
ドキュメントから引用させてもらうと、
カスタムレンダーテクスチャはレンダーテクスチャの拡張機能で、これを使うと簡単にシェーダー付きのテクスチャを作成できます。これは、コースティクス、雨の効果に使われるリップルシミュレーション、壁面へぶちまけられた液体など、あらゆる種類の複雑なシミュレーションを実装するのに便利です。また、カスタムレンダーテクスチャはスクリプトやシェーダーのフレームワークを提供し、部分的更新、または、マルチパスの更新、更新頻度の変更などのさらに複雑な設定をサポートします。
つまり、波形などの複雑なシミュレーションを必要とする演算をシェーダベースで行い、それをテクスチャとして利用できるようにしてくれる機能です。
この機能の面白いところは、updateや初期化などはある程度テクスチャ側の設定項目でまかなえるので、シェーダだけでも完結できる点にあります。
つまりC#スクリプトはいらないということです。
もちろん、細やかな制御をするためにスクリプトから制御することも可能です。
今回の波紋シミュレーションではスクリプトによる更新はしていません。
そしてそれを法線マップとして利用することで冒頭の動画のようなエフェクトを生成しています。
CustomRenderTexture用のcgincがある
さて、では実際に実装を行っていきます。
CustomRenderTextureは前述の通り、シェーダ(マテリアル)を設定するだけでその結果をRenderTextureに保持してくれる便利なものです。
そのため、RenderTextureに保存したい絵を描くためのシェーダを書く必要があります。
(ちなみに、CustomRenderTextureが登場する前は、C#も動員して自分で保存などの処理を書く必要がありました)
まずはCustomRenderTexture向けのシェーダで利用するものを紹介します。
// 専用のcgincファイル
#include "UnityCustomRenderTexture.cginc"
// 専用の定義済みvertexシェーダ関数
#pragma vertex CustomRenderTextureVertexShader
// 専用の構造体
struct v2f_customrendertexture { ... }
// テクスチャサイズを取得
float width = _CustomRenderTextureWidth;
float height = _CustomRenderTextureHeight;
// UV座標を取得
float2 uv = i.globalTexcoord;
// CustomRenderTextureからテクセルをフェッチ
float3 c = tex2D(_SelfTexture2D, uv);
Unityでシェーダを書いたことがある人であればどう使うのかイメージ付くかと思います。 CustomRenderTexture向けにシェーダを書く場合、上記のようにいくつか専用のものが定義されているのでそれを利用します。
これらを使ってCurstomRenderTextureにお絵かきするシェーダを書いていきます。
CustomRenderTexture用シェーダを書く
では実際のシェーダを書いていきます。
波動方程式を解く
CustomRenderTextureで利用するシェーダが分かったところで、実用的な使い方として波動方程式を解いた波形を描いてみたいと思います。
ちなみに、以前自分もQiitaの記事で波動方程式について書いているので、よかったらそちらも参考にしてみてください。(実装はWebGLですが)
上の記事は以下の動画を元に実装したものになります。
波動方程式について、高校数学でも分かるような感じで丁寧に説明してくれていてとても分かりやすいのでオススメです。
なお今回の実装はこちらの凹みさんの記事を参考にさせていただきました。
波動方程式を解くシェーダ(for CustomRenderTexture)
下記シェーダは上記の凹みさんの記事で書かれているものを利用させていただきました。
それを少し整形し、自分がコメントを追記したものです。
Shader "Hidden/WaveShader"
{
Properties
{
_S2("PhaseVelocity^2", Range(0.0, 0.5)) = 0.2
_Atten("Attenuation", Range(0.0, 1.0)) = 0.999
_DeltaUV("Delta UV", Float) = 3
}
SubShader
{
Cull Off
ZWrite Off
ZTest Always
Pass
{
CGPROGRAM
#pragma vertex CustomRenderTextureVertexShader
#pragma fragment frag
#include "UnityCustomRenderTexture.cginc"
half _S2;
half _Atten;
float _DeltaUV;
sampler2D _MainTex;
float4 frag(v2f_customrendertexture i) : SV_Target
{
float2 uv = i.globalTexcoord;
// 1pxあたりの単位を計算する
float du = 1.0 / _CustomRenderTextureWidth;
float dv = 1.0 / _CustomRenderTextureHeight;
float3 duv = float3(du, dv, 0) * _DeltaUV;
// 現在の位置のテクセルをフェッチ
float2 c = tex2D(_SelfTexture2D, uv);
// ラプラシアンフィルタをかける
// |0 1 0|
// |1 -4 1|
// |0 1 0|
float k = (2.0 * c.r) - c.g;
float p = (k + _S2 * (
tex2D(_SelfTexture2D, uv - duv.zy).r +
tex2D(_SelfTexture2D, uv + duv.zy).r +
tex2D(_SelfTexture2D, uv - duv.xz).r +
tex2D(_SelfTexture2D, uv + duv.xz).r - 4.0 * c.r
)) * _Atten;
// 現在の状態をテクスチャのR成分に、ひとつ前の(過去の)状態をG成分に書き込む。
return float4(p, c.r, 0, 0);
}
ENDCG
}
}
}
これを適切にCustomRenderTextureにセットすると以下のようにシミュレーションが進んでいきます。

CustomRenderTextureのセットアップ
シェーダが書けたところで、実際に使用するためにセットアップを行っていきます。
CustomRenderTextureの生成
まずはCustomRenderTextureを生成します。
生成には以下のようにメニューから生成することができます。
CustomRenderTexutreの設定
生成したCustomRenderTextureのインスペクタを見ると以下のような設定項目があります。
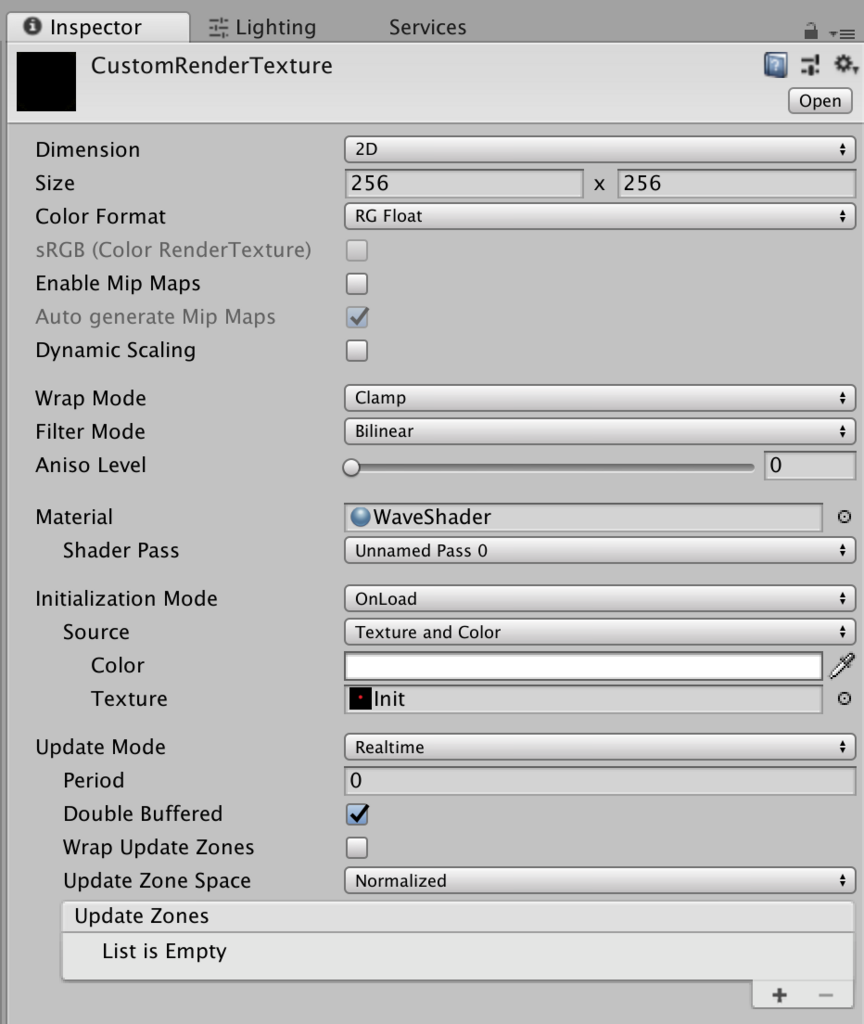
設定項目抜粋
いくつかの設定項目について見ていきます。
Size
CustomRenderTextureのサイズです。
Color Format
今回は凹みさんの記事にならって「RG Float」としています。
これは、現在の波の高さをR要素に、ひとつ前の波の高さをG要素に格納して計算を行うためです。
Material
CustomRenderTextureで使用するシェーダを適用したマテリアルを設定します。
サブ項目に「Shader Pass」がありますが、これは複数パスを定義した場合に、どのパスを利用するか選択できるようになっています。
Initialize Mode
初期化モード。OnLoadとすることで、起動時に初期化されます。
スクリプトから制御する場合は「OnDemand」を選択します。
サブ項目として「Source」があります。
設定できる内容は「Texture and Color」か「Material」があります。
今回は初期化をテクスチャから指定しています。
その場合は初期化に利用するテクスチャを設定する必要があります。
Update Mode
テクスチャの更新に関する設定です。
サンプルでは「Realtime」を設定しています。
こうすることで、スクリプトなしに自動的に更新が行われるようになります。
なお、スクリプトから制御したい場合はこちらも「OnDemand」を選択します。
Double Buffered
ダブルバッファのオン/オフ。
これをオンにすることで、テクスチャの情報をピンポンするように更新することができるようになります。
バンプマップに関して
以上でCustomRenderTextureに関する話はおしまいです。
今回の例ではシミュレーションした波形を利用してバンプマップを行っています。
ただ、シミュレーションした結果はRG要素しかない上に、それぞれのチャンネルはHeightMapとなっているためそのままでは法線マップとして利用できません。
そのため、取得したHeightMapから法線を計算して利用する必要があります。
バンプマップとは
法線マップを使ってポリゴンに凹凸があるように見せる処理です。
以前、Qiitaの記事にも書いたのでよかったら見てみてください。
なお、今回は法線をハイトマップから計算で求めて適用するための方法について書いていきます。
法線をハイトマップから計算で求める
ということで、法線の計算についても書いておきたいと思います。
法線の計算にあたっては、以下のふたつの記事を参考にさせていただきました。
法線は接ベクトルに垂直
接ベクトルをWikipediaで調べると以下のようにあります。
数学において、接ベクトル(英: tangent vector)とは、曲線や曲面に接するようなベクトルのことである。
そして、参考にさせていただいた記事(t-pot『動的法線マップ』)から説明を引用させていただくと、
法線ベクトルの求め方ですが、接ベクトルが法線ベクトルに直行することを利用します。 今回の場合は、高さ情報だけしか変化しないので、X軸及びZ軸の方向に関する高さの偏微分が接ベクトルの方向になります。
ということ。
つまり、接ベクトルをX軸およびZ軸に対して求め、それの外積を取ることで法線を求める、ということです。
図にすると以下のようなイメージです。
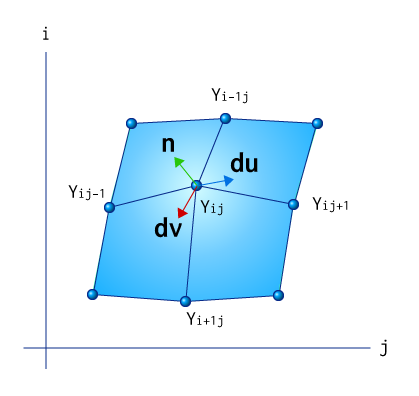
数式にすると以下のようになります。
よって、これを利用して以下のように法線を求めることができます。
float3 du = (1, dyx, 0) float3 dv = (0, dyz, 1) float3 n = normalize(cross(dv, du))
実装
コードにすると以下のようになります。(一部抜粋)
// _ParallaxMap_TexelSizeは、テクスチャサイズの逆数 // テクセルの「ひとつ隣(シフト)」分の値を計算する float2 shiftX = float2(_ParallaxMap_TexelSize.x, 0); float2 shiftZ = float2(0, _ParallaxMap_TexelSize.y); // 現在計算中のテクセルの上下左右の隣のテクセルを取得 float3 texX = tex2D(_ParallaxMap, float4(i.uv.xy + shiftX, 0, 0)) * 2.0 - 1; float3 texx = tex2D(_ParallaxMap, float4(i.uv.xy - shiftX, 0, 0)) * 2.0 - 1; float3 texZ = tex2D(_ParallaxMap, float4(i.uv.xy + shiftZ, 0, 0)) * 2.0 - 1; float3 texz = tex2D(_ParallaxMap, float4(i.uv.xy - shiftZ, 0, 0)) * 2.0 - 1; // 偏微分により接ベクトルを求める float3 du = float3(1, (texX.x - texx.x), 0); float3 dv = float3(0, (texZ.x - texz.x), 1); // 接ベクトルの外積によって「法線」を求める float3 n = normalize(cross(dv, du));
実装は難しい点はありません。
上下の高さ差分と、左右の高さ差分からそれぞれ勾配(接ベクトル)を求め、その2つのベクトルから外積を求めるだけです。
法線は接ベクトルと垂直なので、これで無事、法線が計算できたことになりますね。
最後に、バンプマップを行ったシェーダの全文を載せておきます。
Shader "Unlit/HightMapNormal"
{
Properties
{
_Color("Tint color", Color) = (1, 1, 1, 1)
_MainTex("Texture", 2D) = "white" {}
_ParallaxMap("Parallax Map", 2D) = "gray" {}
}
SubShader
{
Tags { "RenderType" = "Transparent" "Queue" = "Transparent" }
LOD 100
GrabPass { }
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
#include "Lighting.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float4 vertex : SV_POSITION;
float4 uvgrab : TEXCOORD1;
float3 worldPos : TEXCOORD2;
};
sampler2D _MainTex;
sampler2D _ParallaxMap;
sampler2D _GrabTexture;
float4 _MainTex_ST;
fixed4 _Color;
float2 _ParallaxMap_TexelSize;
v2f vert(appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.worldPos = mul(UNITY_MATRIX_MV, v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
#if UNITY_UV_STARTS_AT_TOP
float scale = -1.0;
#else
float scale = 1.0;
#endif
o.uvgrab.xy = (float2(o.vertex.x, o.vertex.y * scale) + o.vertex.w) * 0.5;
o.uvgrab.zw = o.vertex.zw;
return o;
}
fixed4 frag(v2f i) : SV_Target
{
float2 shiftX = float2(_ParallaxMap_TexelSize.x, 0);
float2 shiftZ = float2(0, _ParallaxMap_TexelSize.y);
float3 texX = tex2D(_ParallaxMap, float4(i.uv.xy + shiftX, 0, 0)) * 2.0 - 1;
float3 texx = tex2D(_ParallaxMap, float4(i.uv.xy - shiftX, 0, 0)) * 2.0 - 1;
float3 texZ = tex2D(_ParallaxMap, float4(i.uv.xy + shiftZ, 0, 0)) * 2.0 - 1;
float3 texz = tex2D(_ParallaxMap, float4(i.uv.xy - shiftZ, 0, 0)) * 2.0 - 1;
float3 du = float3(1, (texX.x - texx.x), 0);
float3 dv = float3(0, (texZ.x - texz.x), 1);
float3 n = normalize(cross(dv, du));
i.uvgrab.xy += n * i.uvgrab.z;
fixed4 col = tex2Dproj(_GrabTexture, UNITY_PROJ_COORD(i.uvgrab)) * _Color;
float3 lightDir = normalize(_WorldSpaceLightPos0 - i.worldPos);
float diff = max(0, dot(n, lightDir)) + 0.5;
col *= diff;
float3 viewDir = normalize(_WorldSpaceCameraPos - i.worldPos);
float NdotL = dot(n, lightDir);
float3 refDir = -lightDir + (2.0 * n * NdotL);
float spec = pow(max(0, dot(viewDir, refDir)), 10.0);
col += spec + unity_AmbientSky;
return col;
}
ENDCG
}
}
}
このシェーダのマテリアルを平面に適用することで、冒頭の動画の効果を得ることができます。
参考記事
その他、参考になった記事を載せておきます。