概要
以前書いた粒子法を用いた流体シミュレーションをさらに発展させ近傍探索を行って最適化をしています。
その中で使っている『バイトニックソート』というソートについてまとめたいと思います。
本記事は近傍探索を実装する上でのサポート的な記事です。
近いうちに近傍探索の実装についても書こうと思っています。
なお、参考にさせていただいた記事は流体シミュレーション実装を参考にさせていただいた@kodai100さんが書いている記事です。
内容は近傍探索についてですがその中でバイトニックソートについての言及があります。
ちなみに流体シミュレーション自体についても記事を書いているので興味がある方はご覧ください。
バイトニックソートとは
Wikipediaによると以下のように説明されています。
バイトニックマージソート(英語: Bitonic mergesort)または単にバイトニックソート(英語: Bitonic sort)とは、ソートの並列アルゴリズムの1つ。ソーティングネットワークの構築法としても知られている。
このアルゴリズムはケン・バッチャー(英語: Ken Batcher)によって考案されたもので、このソーティングネットワークの計算量はn個の要素に対して、サイズ(コンパレータ数=比較演算の回数)は
、段数(並列実行不可能な数)は
となる[1]。各段での比較演算(n/2回)は独立して実行できるため、並列化による高速化が容易である。
自分もまだしっかりと理解できてはいませんが、ソーティングネットワークを構築することで配列の中身を見なくともソートができる方法のようです。
この配列の中を見なくてもというのがポイントで、決められた順に処理を実行していくだけでソートが完了します。
言い換えると並列に処理が可能ということです。
並列化による高速化が容易である。
と言及があります。
GPU(コンピュートシェーダ)によって並列に計算する必要があるためこの特性はとても重要です。
ロジックを概観する
まずはWikipediaに掲載されている以下の図を見てください。
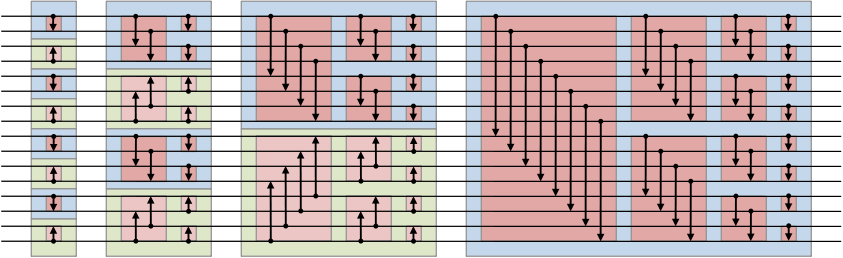
最初はなんのこっちゃと思いましたが、ひとつずつ見ていけばむずかしいことはしていません。
まずぱっと目に着くのは線と色のついた各種ボックスだと思います。
この図が言っているのは配列の中身が16要素あり、それをソートしていく様を示しています。
一番左が初期状態で、一番右がソートが完了した状態です。
よく見ると横に長く伸びる線が16本あることに気づくと思います。
これが配列の要素数を表しています。
余談ですが、なぜこういう図なのかと言うと。
ソーティングネットワーク自体がこういう概念っぽいです。
横に伸びる線をワイヤー、矢印の部分がコンパレータと呼ばれます。
そしてワイヤーの左からデータを流すと、まるであみだくじの要領でソートが完了します。
そのためにこういう図になっているというわけなんですね。
ソートされていく様子はあみだくじを想像するといいかもしれません。
左からデータが流れてきて、決まったパターンでデータが入れ替わっていき、最後にソートが完了している、そんなイメージです。
このデータが入れ替わっていく部分は矢印が表しています。
また矢印の向きは降順・昇順どちらに値を入れ替えるかを表しています。
並列可能部分と不可能部分
まず注目すべきはブロックによって区切られている点です。
以下の図をご覧ください。

メインブロックと書かれたところが大きく4つに分かれています。
そしてそのメインブロックの中にサブブロック郡があります。
ここで注意する点は並列計算可能な部分と並列計算不可能な部分がある点です。
図を見てもらうと分かりますが、メインブロック内の矢印に着目するとそれぞれは独立して処理を行えることが分かります。
どの矢印から処理を開始しても結果は変わりません。
しかしメインブロック自体の計算順序を逆にしてしまうと結果が異なってしまいます。
これは並列実行できないことを意味しています。
今回の目的はGPUによって並列計算を行わせることなのでここの把握は重要です。
つまりメインブロックは並列不可、サブブロックは並列可ということです。
計算回数
次にブロックの処理順について法則を見てみましょう。
メインブロックは全部で4つあります。そして配列数は16です。
この関連性は(
=16)から来ています。
これは推測ですが、バイトニックの名前の由来はこの2進数から来ているのかもしれません。
さて、ではサブブロックはどうでしょうか。
サブブロックにも法則があります。
それは左から順に1, 2, 3, 4, ...と数が増えていることです。
この法則はコードを見てみると分かりやすいです。
for (int i = 0; i < 4; i++)
{
for (int j = 0; j <= i; j++)
{
// ソート処理
}
}
外側のforループがメインブロックのループを表していて、内側のループがサブブロックのループを表しています。
そして内側のループは外側のループが回るたびに回数が増えていく形になっています。
外側のループが1回なら内側も1回だけ実行され、外側の2ループ目は内側は2回ループする、という具合です。
なので外側のループが回るたびに内側のループの回数が増加していくというわけなんですね。
計算最大回数
今回は要素数が16なので4でしたが、これが32なら5回ループが回るということですね。
もちろん、内側のループもそれに応じて増えていきます。
メインブロックの最大計算回数は要素数が2の何乗かに依るわけです。
ちなみに感の良い方ならお気づきかもしれませんが、2のべき乗で計算がされるということはそれ以外の要素数ではソートが行えないことを意味しています。
なのでもし要素数が2のべき乗以外の数になる場合はダミーデータなどを含めて2のべき乗に揃える必要があります。
矢印の意味
さらに詳細を見ていきましょう。
次に見るのは矢印です。
この矢印は配列内の要素を入れ替える(Swapする)ことを意味しています。
矢印なので向きがありますね。これは昇順・降順どちらに入れ替えるかを示しています。
よく見ると青いブロック内は昇順、緑のブロック内は降順に入れ替わっていることが分かります。
そして図の通りに入れ替えを進めていくと最終的にソートが完了している、というのがバイトニックソートです。
ひとつの解説だけだと解像度が足らないので別の記事でも探してみると、以下の記事と画像が理解を深めてくれました。
画像を引用させてもらうと以下のような感じでソートが進んでいきます。


言っていることはWikipediaと同じですが実際の数値が並び変えられていくのでより理解が深まるかと思います。
ちなみにこの入れ替え手順先に示したコード通りになっているのが分かります。
各配列の下に添えられている数字を見ると2のべき乗の部分が0, 1, 0, 2, 1, 0と変化しているのが分かると思います。
これをグループ化して見てみると[0], [1, 0], [2, 1, 0]ということですね。
外側のループ回数が増えるにつれて内側のループが増えていくということと一致しています。
比較する対象の距離と方向を求める
さて、ループについては把握できたかと思います。
次に見るのはどの要素同士を入れ替えるかという点です。
入れ替える距離はループ数によって決まる
ループの仕方が分かっても、闇雲に配列の内容を入れ替えたのでは当然ソートはできません。
ではどういうルールで入れ替えていけばいいのでしょうか。
その答えは以下の計算です。
public static void Kernel(int[] a, int p, int q)
{
int d = 1 << (p - q);
for (int i = 0; i < a.Length; i++)
{
bool up = ((i >> p) & 2) == 0;
if ((i & d) == 0 && (a[i] > a[i | d]) == up)
{
int t = a[i];
a[i] = a[i | d];
a[i | d] = t;
}
}
}
public static void BitonicSort(int logn, int[] a)
{
for (int i = 0; i < logn; i++)
{
for (int j = 0; j <= i; j++)
{
Kernel(a, i, j);
}
}
}
距離に関しては以下の式で求めています。
// distanceのd int d = 1 << (p - q);
ここでpは外側のループ、qは内側のループの回数が渡ってきます。
これを引き算の部分だけ見てみると、ループが進むに連れて以下のように計算されます。
0 - 0 = 0 1 - 0 = 1 1 - 1 = 0 2 - 0 = 2 2 - 1 = 1 2 - 2 = 0 ...
引き算の結果は1bitをどれだけ左にシフトするかの数値なので、つまりは2を何乗するかを示しているわけですね。
これを把握した上で改めて先ほどの図を見てみると、確かにそう変化していっているのが分かると思います。


昇順・降順は2bit目が立っているかで切り替える
昇順・降順を決めている計算は以下の部分です。
for (int i = 0; i < a.Length; i++)
{
bool up = ((i >> p) & 2) == 0;
// 後略
}
iは要素数分ループする回数を示しています。そしてpは前述の通り、外側のループ、つまりメインブロックの計算回数を示しています。
つまり、全要素をループさせ、かつそのループ回数をメインブロックの計算回数値だけ右にシフトし、そのときのビット配列の2bit目が立っているか否かで昇順・降順を切り替えているわけですね。(ちなみに2bit目が立っている場合は降順)
ちょっとしたサンプルを書いてみました。
以下のpaizaのコードを実行すると、上の図の昇順・降順の様子と一致していることが分かるかと思います。
(サンプルコードの↓が昇順、↑が降順を表しています)
Swap処理
最後に、どの場合にどこと入れ替えるかの処理について見てみましょう。
bool up = ((i >> p) & 2) == 0;
if ((i & d) == 0 && (a[i] > a[i | d]) == up)
{
int t = a[i];
a[i] = a[i | d];
a[i | d] = t;
}
最初の行のupのは昇順か降順かのフラグです。
続くif文が実際にSwapをするかを判定している箇所になります。
条件が2つ書かれているのでちょっと分かりづらいですが、分解してみると以下の2つを比較しています。
// ひとつめ (i & d) == 0
// ふたつめ (a[i] > a[i | d]) == up
ひとつめは要素の位置とdとの理論積になっていますね。
ふたつめは、配列の要素のふたつの値を比較し、upフラグの状態と比較しています。
これは昇順か降順かを判定しているに過ぎません。
問題は右側の要素へのアクセス方法ですね。
a[i | d]はなにをしているのでしょうか。
これらが意味するところは以下の記事がとても詳しく解説してくれています。
この記事から引用させてもらうと、
あるインデックスに対してそれと比較するインデックスはdだけ離れています。そのため2つのインデックスをビットで考えると値は
p - qビット目の値が0か1かの違いだけになります(一番右端のビットを0ビット目として数えています)。配列の先頭に近いほうにあるインデックスをiとすると比較対象のインデックスはp - qビット目が1になるのでそのインデックスはi | dになります。つまり、if文内の(i & d) == 0は配列の先頭に近いほうにあるインデックスかどうかを確認しており、x[i] > x[i | d]で2つの値の大小を確認していることになります。
と書かれています。
文章だけだとちょっと分かりづらいですが、実際にbitを並べて図解してみると分かりやすいと思います。
試しに要素数8の場合で書き下してみると、
000 = 0 001 = 1 010 = 2 011 = 3 100 = 4 101 = 5 110 = 6 111 = 7
というふうになります。値の意味は配列の添字です。(要素数8なので0 ~ 7ということです)
以下の部分を考えてみましょう。
あるインデックスに対してそれと比較するインデックスはdだけ離れています。
仮にd = 1 << 0だとするとdの値は1です。つまりひとつ隣ということですね。
000 = 0 ┐ 001 = 1 ┘ 010 = 2 ┐ 011 = 3 ┘
比較する対象はこうなります。そして引用元では、
そのため2つのインデックスをビットで考えると値は
p - qビット目の値が0か1かの違いだけになります(一番右端のビットを0ビット目として数えています)。
と書かれています。上の例ではp - q == 0としているので、つまりは一番右側(0番目)のビットの違いを見れば良いわけです。
見てみると確かに違いは0ビット目の値の違いだけであることが分かります。
冗長になるのでこれ以上深堀りはしませんが、実際に書き下してみると確かにその通りになるのが分かります。
そしてここを理解するポイントは以下です。
- 比較対象のうち、配列の先頭に近い方のインデックスの場合のみ処理する
- 先頭に近いインデックスだった場合は、そのインデックスとそのインデックスから
dだけ離れた要素と比較する
ということです。
まぁ細かいことは置いておいても、for文で全部を処理している以上、重複してしまうことは避けられないので、それをビットの妙で解決しているというわけですね。
これを一言で言えば、先頭のインデックスだった場合は、そのインデックスとdだけ離れたインデックス同士を比較するということです。
コード全体
最後にコード全体を残しておきます。
以下はC#で実装した例です。コード自体はWikipediaのJavaの実装をそのまま移植したものです。
// This implementation is refered the WikiPedia
//
// https://en.wikipedia.org/wiki/Bitonic_sorter
public static class Util
{
public static void Kernel(int[] a, int p, int q)
{
int d = 1 << (p - q);
for (int i = 0; i < a.Length; i++)
{
bool up = ((i >> p) & 2) == 0;
if ((i & d) == 0 && (a[i] > a[i | d]) == up)
{
int t = a[i];
a[i] = a[i | d];
a[i | d] = t;
}
}
}
public static void BitonicSort(int logn, int[] a)
{
for (int i = 0; i < logn; i++)
{
for (int j = 0; j <= i; j++)
{
Kernel(a, i, j);
}
}
}
}
public class Example
{
public static void Main()
{
int logn = 5, n = 1 << logn;
int[] a0 = new int[n];
System.Random rand = new System.Random();
for (int i = 0; i < n; i++)
{
a0[i] = rand.Next(n);
}
for (int k = 0; k < a0.Length; k++)
{
System.Console.Write(a0[k] + " ");
}
Util.BitonicSort(logn, a0);
System.Console.WriteLine();
for (int k = 0; k < a0.Length; k++)
{
System.Console.Write(a0[k] + " ");
}
}
}
実際に実行する様子は以下で見れます。
まとめ
まとめると、バイトニックソートは以下のように考えることができます。
- 比較する配列の要素は常にふたつ
- 比較対象はビット演算によって求める
- 昇順・降順の判定もビットの立っている位置によって決める
- 配列の要素の比較重複(0 -> 1と0 <- 1という向きの違い)もビットの位置によって防ぐ
分かってしまえばとてもシンプルです。
が、理解もできるし使うこともできるけれど、これを思いつくのはどれだけアルゴリズムに精通していたらできるんでしょうか。
こうした先人の知恵には本当に助けられますね。