Unityで流体シミュレーション～粒子法編～

はじめに

以前に、格子法を用いた2次元の流体シミュレーションについて概念編と実装編に分けて2つの記事を書きました。

しかし格子法は、その定義領域の範囲を越えてしまうと計算ができなくなってしまうという問題があります。特に今回は3Dに拡張し、AR/VR内で利用することを目論んでいるのでうまく行かない可能性があります。
そこで今回は別の手法である『粒子法』を用いて流体シミュレーションを行う方法について調べてみたのでそれをまとめていきます。

今回の実装は特に、Unity Graphics Programming vol.1に掲載されているSPH法の解説とGitHubにアップされているサンプルを元にしました。

ここで書くことはあくまで自分の理解のためのメモであり、物理的・数学的見地からの詳細を解説しているものではありません。
また、多くの部分を書籍からの引用に頼っています。予めご了承ください。

Unity Graphics Programmingシリーズは無料でダウンロードできます

なお、上記書籍のシリーズは無料でPDFにて公開されています。
vol.4まであるので読み応えがあります。元の情報を参照されたい方は以下からダウンロードしてください。

github.com

これを元に実装してみたのが以下です。

パラメータを調整して、2x2x2くらいの容量でのシミュレーションで違和感ない感じにしてみた。https://t.co/mzVVtTw2DB #Unity #fluid #Shader
— edom18@AR / MESON (@edo_m18) 2020年5月7日

Table of contents

はじめに
粒子法の概要
- オイラー的視点とラグランジュ的視点での微分の違い
そしてそれぞれの変数分同じことをやれば上記式になります。
SPH実装のフロー
重み関数
密度の計算
- Poly6関数
圧力項の計算
- ∇Spiky
- Tait方程式による粒子圧力の事前計算
粘性項の計算
- △Viscosity
外力項の計算
実装に向けて
- コンピュータによる計算のフロー
まとめ
近傍探索について
その他参考にした記事

粒子法の概要

以前書いた格子法と今回の粒子法では『視点の違い』があります。

格子法の視点は格子で、計算対象を格子に区切って計算を行います。
一方粒子法の視点は粒子で、計算対象を粒子そのものにして計算を行います。

ざっくりとしたイメージで言うとそれぞれの違いは以下です。

格子法は観測地点（各格子）に定点カメラを設置してその『場』の動きを計算します。
粒子法では粒子を追跡するカメラを用意して計算します。

そしてこれらの違いをそれぞれ、オイラー的視点とラグランジュ的視点と呼びます。

オイラー的視点が格子法、ラグランジュ的視点が粒子法です。

参考にさせていただいた書籍から図を引用させていただくと以下のようなイメージの違いになります。

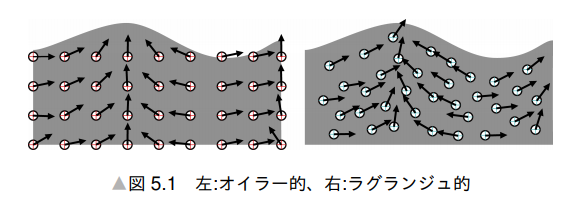
f:id:edo_m18:20200523194416p:plain

左の図が示している丸は粒子ではなく、各格子の現在の速度場ベクトルを表しています。（なので各点間の距離が均一になっています）
一方、右の図は粒子そのものを観測しているため各点自体が現在の粒子の位置を表しています。（なので各点間の距離がバラバラになっています）

オイラー的視点とラグランジュ的視点での微分の違い

オイラー的視点とラグランジュ的視点では微分の演算の仕方が異なるようです。
なぜ突然微分の話なんだ、と思うかもしれませんが、流体の方程式は一発で粒子の位置を求めることはできず、微分して得られた速度を元に徐々に更新していくことで求めます。
そのため現在と過去の状態から微分によって速度を求め、次の位置を求める必要があります。なので微分の話なのです。

そして違いをとてもざっくり書いてしまうと、物理量に対して以下の式の違いがあります。

オイラー的視点での微分

これは、時刻tにおける位置 $\vec{x}$ の物理量を表しています。これを時間微分すると以下の式が得られます。

なんてことはない、偏微分の式ですね。

ラグランジュ的視点での微分

一方、ラグランジュ的視点では以下の式が物理量を表します。

これを微分すると、最終的に以下の式が得られます。

※ この式が出てくる理由は、おそらく全微分によるものだと思います。全微分のざっくりとした説明はこちら。

余談

全微分について上記記事から引用させてもらうと、

接線の傾き（つまり、関数を１次関数で近似したときの傾き）が微分です。すなわち、
$f(x_0+h)=f(x_0)+ah+o(h)$

とあります。
つまり、とある関数に対して $x_0$ 付近で1次関数で近似したものということですね。（接線の傾きということは直線＝1次関数）

そして全微分の係数（a）は偏微分で求まります。（同様に、多数変数の場合はb、cと変数分、係数が増え、それぞれの変数の偏微分で求まります）
（例えば $a = \frac{\partial f}{\partial x}$ ）

これを用いて2変数の場合は

となります。このことから、偏微分の値を $\sum$ で合計している理由が分かりますね。
おそらく $\frac{\partial x_i}{\partial t}$ は、時間による偏微分なのでとある軸方向の微小量を求めているのだと思います。
なので上記式で言うところのdxっていうことですね。

ちなみに記事内で言及されている以下の点、

例えば、３変数関数 $f(x, y, z) = x^2 + y^3 + yz$ を $(x_0,y_0,z_0)$ の近くで一次近似すると、
$f(x, y, z) ≒ f(x_0, y_0, z_0) + 2x_0(x − x_0) + (3y^2_0 + z_0)(y − y_0) + y_0(z − z_0)$ となります。
（なぜ上式のようになるのか、計算は後ほど「全微分と偏微分の関係」で述べます）

$x − x_0 = \Delta x$ などと置いて上式を移項すると、 $f(x_0 + \Delta x, y_0 + \Delta y, z_0 + \Delta z) − f(x_0, y_0, z_0) ≒ 2x_0 \Delta x + (3y^2_0 + z_0)\Delta y + y_0 \Delta z$ となります。

これはこう解釈できます。

$f(x_0, y_0, z_0)$ の近くで一次近似ということは、その面に対しての接線ということです。
つまり、その地点においては線とみなせる＝微小量変化した、というわけですね。

そして「xをどれくらい変化させたら関数にどういう変化をもたらすか」というのは偏微分で求まる微分係数です。

偏微分を用いて変化率を求めると $\frac{\partial f}{\partial x} = 2x$ です。
そして増加量は $\Delta x$ なので $2x_0 \Delta x$ になりますね。

そしてそれぞれの変数分同じことをやれば上記式になります。

閑話休題。

さて、両者の違いが分かりますか？

オイラー的視点の式が意味するのは『位置が固定である』という事実です。なので式の中の位置ベクトル（ $\vec{x}$ ）はただの変数になっていますね。

一方、ラグランジュ的視点の式が意味するのは『位置は変動する』という事実です。なので位置ベクトルは時間の関数（ $\vec{x}(\vec{x}_0, t)$ ）になっています。

少しだけ補足すると、とある時間の位置ベクトル（ $\vec{x}$ ）は初期位置（ $\vec{x}_0$ ）と時間tを引数に取る関数となっています。

粒子法のナビエ・ストークス方程式

流体シミュレーションをしようとすると必ず登場するナビエ・ストークス方程式。
これを解くことで流体をシミュレーションすることができるようになります。つまり、流体シミュレーションにおいて一番重要な部分です。

粒子法のナビエ・ストークス方程式は以下で与えられます。
実際に式を見てもらうと分かりますが、微分の嵐ですねｗ
このことからも微分が重要なことが分かります。

一方、格子法は以下でした。

前の記事で解説した格子法によるナビエ・ストークス方程式と見比べてみると移流項（ $-(\vec{u} \cdot \nabla) \vec{u}$ ）がまるまるなくなっているのが分かるかと思います。
これは、格子法では観測点を『場』に固定して観測している一方で、粒子法は『粒子自体』を観測しているため、そもそも『移流』が発生しないことによります。

ここの導出に関してはちょっとまだしっかり理解しきれていません。詳細については参考にした書籍をご覧ください。

そこでの解説を少しだけ引用させていただくと以下のように記載されています。

前章の格子法で出てきたNS方程式とは少し形が異なりますね。移流項がまるまる抜けてしまっていますが、先程のオイラー微分とラグランジュ微分の関係を見てみると、うまくこの形に変形できることが分かります。粒子法では観測点を流れに沿って移動させますから、NS方程式計算時に移流項を考慮する必要がありません。移流の計算はNS方程式で算出した加速度をもとに粒子位置を直接更新することで済ませる事ができます。

ここ、ちゃんと理解しきれていないのですが、微分の式を見てみるとちょうど $-(\vec{u} \cdot \nabla) \vec{u}$ と同じ形の式が出来ていることが分かります。もしかしたらこれが相殺されてなくなる、ということなのかもしれません。

流体の非圧縮性

実はナビエ・ストークス方程式だけでは解を求めることはできません。これについては前回の「Unityで流体シミュレーションを実装する〜概念編〜」の未知数と式の数のところでも触れていますが、未知数の数に対して式の数が合わないためです。

そのときの文を引用すると、

実は冒頭の式だけではこれを解くことができません。理由は、未知数が4つに対して式が3つしかないためです。式がひとつ足りないんですね。

そこで、一般的な流体の持つ非圧縮性という性質を利用してもうひとつ式を作ります。

ということで式がもうひとつ必要になるわけです。
そこで出てくるのが見出しの『流体の非圧縮性』です。

日常観測できる範囲の液体は非圧縮性を考慮しても問題ないようです。
参考にした書籍では『音速よりも十分に小さい場合』と記載があり、やはり相当特殊な環境下でない限りは非圧縮性を持つものとして考えていいと思います。

非圧縮性は以下の式で表されます。

これは『発散』といい、流体内で湧き出しや消失がない（= 0）ことを意味します。なので非圧縮性。
要は、液体が押されてとある場所に移動した場合、その量と同じ分だけそこにあった液体が別のところに押し出される、という感じでしょうか。
（もしそうならないなら圧縮されていることに他ならないからです）

粒子法の計算の概念

ナビエ・ストークスの導出などは自分の知識ではまだまだできませんので、細かいことについては独自で調べてみてください。
以前に書いた格子法の概念編では色々参考にしたリンクを掲載してるのでそちらも見てみると理解が深まるかもしれません。

ここでは粒子法の計算概念について簡単に書いておきたいと思います。

いったん理論は忘れて、実際の流体に目を向けてみましょう。
みなさんご存知の通り、実際の流体も『分子』によって形成されています。つまり人の目には見えないだけで、実際は細かい粒子が集まってできているというわけですね。

つまり実際の流体も、極論で言えば超超超精細なパーティクルシステムと見なすことができます。
が、現在の科学ではそれらを真面目に計算することなど到底できません。
なので粒子法ではこれを、現在のコンピュータを用いて現実的な時間で計算できるくらいの数に減らすことを考えます。

簡単に言えば、ある程度大きな『粒』として分子をまとめて塊として扱う、ということです。
そして『人間の目に知覚できるくらいの粒子』として見た場合、いわゆる剛体の運動方程式 $m\vec{a} = \vec{f}$ と同じことを各粒子に課すことで粒子を移動させ流体を表現できる、というわけです。（と理解しています）

この『ある程度の塊』として見た場合の粒子では、それぞれ、質量 $m$ 、位置ベクトル $\vec{x}$ 、速度ベクトル $\vec{v}$ 、体積 $V$ を持つと考えることができます。

流体とは、この粒子が様々な力を受けて相互干渉し、移動することで実現されます。
この様々な力は以下に挙げられるものがあります。

外力（重力など）
圧力
粘性力

個別に見ていきましょう。

外力

これが一番分かりやすい力でしょう。
重力は言わずもがな、なにか剛体などがぶつかって力を加えたり、あるいは遮蔽物による反発力などもあるでしょう。そうした『外から与えられる力』がこの外力です。

圧力

圧力は『気圧』『水圧』などの単語からも分かるように、流体同士が及ぼし合う力です。
流体は圧力の高いところから低いところに向かって流れます。

それ以外でも、ある程度安定した状態の流体であっても、粒子間が押し合うため常に圧力は発生しています。
人が水の中に入ると流れがなくても『圧』を感じますよね。

粘性力

圧力はわりとイメージしやすいかと思いますが、粘性力とはなんでしょうか。
粘性力を一言で言うと『周りの粒子への影響力』と言えると思います。

粘性力が高い流体としては、はちみつや溶けたチョコレートなどがイメージしやすいでしょう。
『粘性力が高い』とは、流体の流れを平均化させ（周りに強く影響し）変形しづらくさせる、ということです。

書籍から引用させていただくと

周囲の平均をとるという演算は、ラプラシアンを用いて行うことができます。

とあります。
波動方程式でも周りの平均を取って周りに力を伝搬させていくのにラプラシアンを使いますね。

ちなみにそのあたりについては格子法のナビエ・ストークス方程式の解説のところで少し触れているので参考にしてみてください。

SPH実装のフロー

さて、ざーっと概要を書いてきましたが、ここからは実際の実装について書いていきます。

SPH法では以下のフローを繰り返し行ってシミュレーションしていきます。

重み関数の係数を事前計算（*）
密度を計算
圧力項を計算
粘性項を計算
衝突判定
位置更新

（*） ... (1)は事前計算なので初回のみ計算するだけでOKです。

以下から、ひとつずつ詳しく見ていきます。

重み関数

SPH法を実装していくにあたって、この『重み関数』が重要になります。
重み関数をざっくり一言で言うと『周りの粒子から受ける力の重みを求める関数』です。

前述の通り、各粒子は周りの粒子からの影響を受けて移動します。そしてその影響の受ける度合いを決めるのがこの重み関数です。

そしてナビエ・ストークス方程式の各項を求める際にこの重み関数を利用します。
各項のところで詳細は説明しますが、各項に使われる重み関数はそれぞれ異なったものを利用します。

重み関数の係数を事前計算

重み関数を見ていく・・・前に、まずは全体を通して必要となる「物理量の離散化」を取り上げます。

物理量の離散化

普通の数学では連続した値をそのまま扱って数式を解いていきますがコンピュータではそのままでは計算できません。

コンピュータで計算ができるようにするためには『離散化』が必要となります。
Wikipediaから引用させてもらうと以下のように記述があります。

数学において、離散化 (discretization) 連続関数、モデル、変数、方程式を離散的な対応する物へ移す過程のこと。この過程は普通、それらをデジタルコンピュータ上での数値評価および実装に適したものにするために最初に行われるステップである。

離散化、というとむずかしく聞こえますが、プログラミングで考えるととても簡単な概念です。
つまりコンピュータ上で取り扱える式（＝四則演算のみ）に変換することを言います。

プログラムによる例

Unityを触っている人であれば以下のような計算は一度は行ったことがあると思います。

Vector3 velocity = (currentPosition - previousPosition) / Time.deltaTime;

この処理の意味は『今の位置から前の位置を引いてそれを $\Delta t$ で除算する＝微分』ということですね。

逆にここで求めた速度を使って計算を行うと積分となります。

transform.position += velocity * Time.deltaTime;

コンピュータではこのTime.deltaTimeを使って『1フレーム』を表現し、その『飛び飛びの時間（離散した時間）』で計算を行っているわけです。このことから『離散化』のイメージが湧くかと思います。

そして上で『四則演算のみで計算を行う』と書いたように、上の式はまさに『四則演算だけ』で成り立っているのが分かるかと思います。これが離散化の考え方です。

特に今回の記事での離散化とは、とある点ごと（Unityではフレームごと）に観測し計算していくこと、と考えていいと思います。

重み関数を使った物理量の離散化

SPH法では粒子ひとつひとつが影響範囲を持っていて、他の粒子との距離が近いほど強く影響を受ける、という挙動をします。

前述の書籍から図を引用させていただくと以下のようなグラフになります。

f:id:edo_m18:20200518143342p:plain

中央が盛り上がっているグラフなのが分かるかと思います。つまり、近くの粒子の距離が近づくほど影響が強く、離れるほど影響が小さくなっていくことを図示しています。（そして一定距離以上離れている粒子からの影響は最終的にゼロになります）

SPH法における物理量をΦとすると、重み関数を用いて以下のように離散化されます。

ここで、 $N, m, ρ, h$ はそれぞれ以下の意味になります。

$N$ ... 近傍粒子の集合
$m$ ... 粒子の質量
$ρ$ ... 粒子の密度
$W$ ... カーネル関数（重み関数）
$h$ ... 重み関数の影響半径

ちなみにこちらの記事（SPH法の理論 - SPH法による離散化式）から引用させていただくと以下のように記載があります。

ここで，Nは近傍パーティクルの集合，mはパーティクル質量，sph_eq_rho.gifはパーティクル密度， Wはカーネル関数である．カーネル関数は有効半径hを持ち，有効半径外では0となる(コンパクトサポート)．また，その積分が1となる（ $\int Wd\vec{r} = 1$ ）ように設定される

上式のようにSPHでは物理量を周囲のパーティクルの重み付き和で近似する．そして，物理量の勾配 $\nabla \phi$ はカーネル関数の導関数を用いて表す．

SPH法ではいくつかの異なる重み関数を利用して計算を行っていきます。
その際、各重み関数には決まった係数があり、また毎フレーム同じ値が利用できるので初回に求めてそれを使い回すことができます。

重み関数および係数に関してはこちらの記事に詳しく掲載されています。

www.slis.tsukuba.ac.jp

各重み関数については各項の説明のときに詳細を説明しますが、ひとつ例として上げておきます。

Poly6関数

Poly6と呼ばれる重み関数です。

前述のように、 $h$ はひとつの粒子に注目した際に、その粒子に影響を与える他粒子を見つけるための影響半径です。
要は、その半径の円内にある粒子からのみ影響を受ける、ということを言っているわけです。

そして影響を受ける粒子の場合には(h² - r²)³という計算で求められる値を重みとする、というわけです。
ちなみにαはさらに場合分けされていますが、これは2Dと3Dで異なる値を利用することを意味しています。

密度の計算

ここからは各フローを詳細に見ていくことにしましょう。

まずは密度を計算できるように離散化します。密度の離散化は以下の式で与えられます。

そして密度計算で利用する重み関数は以下のPoly6関数です。

Poly6関数

Poly6は上で説明したものと同じです。これは密度計算にのみ使われます。再掲すると以下で示される関数です。

今回は3D版として実装したので3D版の係数を使います。

圧力項の計算

次は圧力項を計算します。
圧力項も密度と同様、離散化して計算を行います。

なお、こちらの記事から引用させていただくと以下のように説明されています。

圧力項は圧力値の勾配で構成される．勾配値用の離散化式を用いることで圧力項を離散化することができるが，粘性拡散項と同様にasymmetricの問題が出るので，
// 中略。引用元では離散化の式が書かれている
と圧力の平均値を用いている．

ということで、圧力の平均値を利用するようです。

圧力項の離散化の式は以下で与えられます。

そして圧力計算でも専用の重み関数を使います。また式から分かるように、重み関数の勾配をとったものを利用します。

∇Spiky

Spikyと呼ばれる重み関数に∇を作用させたもの。

これも2D版と3D版があり、3D版の係数を利用します。

Tait方程式による粒子圧力の事前計算

書籍によると各粒子単体の圧力を『Tait方程式』という方程式を用いて事前に計算しておくようです。

またこちらの記事では以下のように説明されています。

非圧縮性を強制するもっともポピュラーな方法はポアソン方程式 $\nabla^{2} p=\rho \frac{\nabla u}{\Delta t}$ を解くことであるが，そのためには巨大な線形システムを解く必要があり，非常に計算時間がかかる(MPS法ではこれをやっている)．

[Becker2007]ではTait方程式を用いることである程度の非圧縮性を確保している．

要は、処理負荷が高いから簡単な式に置き換えちゃいましょう、ということ。

そしてTait方程式は以下で与えられます。

ここで $\gamma = 7$ です。
またBは圧力定数で、以下の式で求められます。

ここで $c_{s}^2$ は音速です。

これらの詳細については以下の記事を参考にしてください。

www.slis.tsukuba.ac.jp

粘性項の計算

次に粘性項を計算します。

圧力同様、こちらの記事から引用させていただくと以下のように説明されています。

粘性項は流体の速度により構成される．速度 $\vec{u}$ のラプラシアンをそのまま離散化すると(離散化式の $\phi$ を $\vec{u}$ で置き換える)，あるパーティクルiからjに与える力とjからiへの力が異なる(asymmetric)．このままでは速度の速いパーティクルは遅いパーティクルに影響を与えるが，その逆の影響力が小さくパーティクル速度が発散してしまう．

粘性力は流体の速度差に依存すると考えて，symmetricに作用するようにしたのが以下の式である．

ということで、得られる離散化の式は以下です。

△Viscosity

Viscosity重み関数にラプラシアンを作用させたもの。

外力項の計算

最後は外力項です。
ただ外力項はその名の通り、粒子間の影響ではなく完全に外部からの力になります。
代表的なのは重力でしょう。なにもしていなくても下に引きつけられる力がかかります。

それ以外では、例えば剛体にぶつかった場合などの反発力などもあるでしょう。

概念としては粒子の外になるので、ここでの説明は割愛します。
次回は実装編（3D版編）を書く予定なのでそちらで書きたいと思います。

実装に向けて

さて、以上まででSPH法によるナビエ・ストークス方程式の各項を求める準備が整いました。
それぞれの項をしっかり解こうとすると一筋縄では行きませんが、（正直、今の自分ではまったくできません）コンピュータでは離散化された（四則演算だけで計算可能な）シンプルな式に置き換え、それを毎フレーム足し込んでいくだけで結果を表示することができます。

コンピュータによる計算のフロー

あとはここまで解説してきた各項の離散化された式をまとめ上げて計算してやればいいことになります。
コンピュータによる計算のフローは以下になります。

各項の重み関数の係数を事前計算
密度を更新
粒子単体の圧力の計算
圧力項の更新
粘性項の更新
圧力・粘性・密度を用いて加速度を計算
求まった加速度を元に速度を計算
求まった速度から粒子の位置を更新

ナビエ・ストークス方程式での計算は1～5までで、それ以降は求まった速度から粒子の位置を更新してやるだけです。

実際のコードを抜粋すると以下のように位置を計算しています。

velocity += _TimeStep * acceleration;
position += _TimeStep * velocity;

// Update particles buffer.
_ParticlesBufferWrite[P_ID].position = position;
_ParticlesBufferWrite[P_ID].velocity = velocity;

普通の剛体の位置計算と変わらないのが分かるかと思います。
この『速度』を求めるために色々やっていたのがナビエ・ストークス方程式、というわけです。（まぁそもそも式を見たらそう書いてありますしね）

ナビエ・ストークス方程式を再掲すると以下です。

まさに『速度』を求める式ですね。

あとはこれを毎フレーム実行してやれば冒頭の動画のようになる、というわけです。

まとめ

いかがでしょうか。粒子法の概要だけでも伝わってくれれば幸いです。
そして書籍を見た方はお気づきかと思いますが、ベースは書籍で書かれていることほとんどそのままです。

そこに、自分なりのメモや理解、そして別途参考にした記事などのリンクを引用させてもらいました。
（基本的に自分の理解を助けるために頭の中の整理を記事にしたものなのでそのあたりはご了承ください）

次は実装編、と行きたいところですが、実装に関しては参考にさせていただいた書籍を見たほうがいいでしょう。
あるいは、親切にも、動作するサンプルをGitHubにアップしてくださっているので、動くものを見ながら理解していくのがいいと思います。（自分もそうしました）

なので次回はちょっと視点を変えて、2D版としてアップされているサンプルを3D化した部分についてメモを添えつつ、コードをざっくり解説しようかなと思っています。

近傍探索について

さてまとめたあとになんですが、今回サンプルとして上がっているものは最適化を行わず理解のしやすさを重視しているため、そのままだとだいぶFPSがきびしい感じになります。

なぜかと言うと、粒子法では粒子は自由に動き回ることができるため、影響のある近傍の粒子を集めて計算を行う必要があります。

今回の実装では書籍に習って愚直に全部の粒子に対して距離計算を行っています。（というか、サンプルに手を加えていないとも言う）
そのため、実際に公開しているサンプルを実行してもらうと分かりますが、8,000パーティクルも出すとだいぶFPSが落ちてしまいます。

自分のPCではGTX1080を搭載していますが、それでも60FPSを下回るくらいにFPSが落ちてしまいます。

通常、こうした『全粒子に対する計算』のオーダーは[tex: O(n²)]となり、粒子数の2乗に比例して計算負荷が高まっていきます。
つまり今回の8,000パーティクル程度でもその2乗値、つまり64,000,000回の計算となってしまいます。
いくらGPUによって並列計算していると言えどもかなりの高負荷になることが分かるかと思います。

そのため、『近傍探索』を最適化し、計算回数を抑える工夫をしなければなりません。
この近傍探索についても、重み関数で紹介したサイトに解説があります。
また、今回の書籍を執筆された@kodai100さんがQiitaで近傍探索の記事を公開されています。

次はこれらを参考にして近傍探索を最適化したものを実装する予定です。（そして願わくば、自分で作っているARコンテンツに入れ込みたい）

もし興味がある方は以下の記事を参考にしてみてください。

www.slis.tsukuba.ac.jp

qiita.com