はじめに
元記事は、以前自分が英語で書いたものの日本語訳版になります。(自分で書いた英語を翻訳するという初体験w)
概要
今回のこの記事は、Generalized Perspective ProjectionをUnityで実装するための解説記事です。
これが意味するのは、任意の視点からのGeneralized Perspective Projection用のマトリクスを生成する方法を示します。
本実装を行うにあたって以下の論文を参考にさせていただきました。
以下の動画を見ると今回の記事でなにができるかが分かるかと思います。
まず、動画ではカメラに対して垂直になるように回転とプロジェクションをプレーンに適用するところを示しています。
次の動画は任意の視点から、例えば『窓の外』を映し出すようなプレーンの様子です。
今回の動画の実装は、GitHub上にアップしてあるので、実際の挙動を見たい方は以下からcloneしてご覧ください。
アイデア
今回のメインアイデアは、カメラ(ビュー)から垂直に位置するプレーンに対してプロジェクションする、という方法をベースにしています。
それを実現するためにいくつかの点(ポイント)と直行するベクトルを求める必要があります。
コーナーポイントの定義
最初に、スクリーンとなるプレーンのコーナーポイントを定義します。
以下の画像は、各ポイントがどう配置されるかを示しています。

Pa, Pb, Pcの3点を定義しています。
平面上の直行ベクトルを計算する
次に、平面上の直行するベクトルを計算します。
計算自体はとてもシンプルです。すでにコーナーポイントがあるので、これを用いてベクトルを求めます。
計算は以下のようになります。
Vu = (pc - pa).normalized; Vr = (pb - pa).normalized; Vn = Vector3.Cross(vu, vr).normalized;
これを図示すると以下になります。

中心から外れたポイントを計算する
まず、通常の視錐台の状態を確認しておきましょう。

これは、通常の視錐台の注視点がどこにあるかを図示しています。
見て分かる通り、平面の中心に位置していることが分かります。
しかし今回は任意のビューからの視錐台を作る必要があります。
つまり、中心点が動かされた点(Peの正面にある点)を求める必要があります。
図にすると以下のようになります。

当然、この点を求める必要があります。が、すでに計算に必要な情報は揃っているので、それを使って求めます。
まず、カメラ位置から各コーナーポイントへのベクトルを求めます。
Vector3 va = pa - pe; Vector3 vb = pb - pe; Vector3 vc = pc - pe;
これを図示すると以下のようになります。

視錐台の各値を求める
以上までで必要な情報が揃いました。
これらを用いて視錐台の情報(l,r,t,b)を求めます。
各変数の意味は以下の図の通りです。
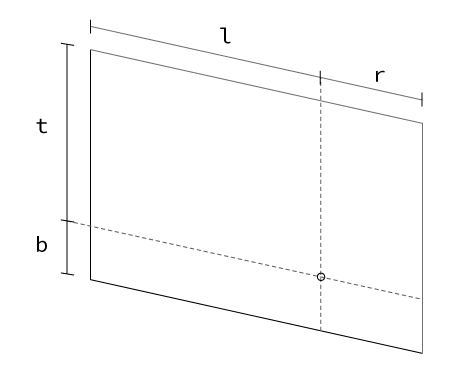
これらの値は以下のように求めることができます。
// Find the distance from the eye to screen plane. float d = -Vector3.Dot(va, vn); // Find the extent of the perpendicular projection. float nd = n / d; float l = Vector3.Dot(vr, va) * nd; float r = Vector3.Dot(vr, vb) * nd; float b = Vector3.Dot(vu, va) * nd; float t = Vector3.Dot(vu, vc) * nd;
さて、ここで登場したdがなんだろうと思ったと思います。
このdはスケールです。near planeまでの距離nに比べてどれくらい差があるか、を示しています。
図にしたほうが分かりやすいと思うので、図示すると以下のようになります。

図には2つの三角形が描かれているのが分かるかと思います。
これらは相似になっています。相似ということはひとつの比率から、その他の辺の比率も求められる、ということです。
今ほしいのは視錐台を生成するためのパラメータです。
そして前述のようにl,r,t,bを求めたいわけです。ただこれはnear plane想定の値である必要があるため、カメラと平面との距離を測り、その比率を掛けたものが、最終的に求めたい値となります。
なので、前述のコードではそれぞれの値にnd(スケール)を掛けていた、というわけです。
さて、これで視錐台を生成するための準備が整いました。
コード解説
前述までの結果を元に視錐台を生成します。まずはコード全文を見てください。
private void UpdateFrustrum()
{
float n = _camera.nearClipPlane;
float f = _camera.farClipPlane;
Vector3 pa = _pa.position;
Vector3 pb = _pb.position;
Vector3 pc = _pc.position;
Vector3 pe = _pe.position;
// Compute an orthonormal basis for the screen.
Vector3 vr = (pb - pa).normalized;
Vector3 vu = (pc - pa).normalized;
Vector3 vn = Vector3.Cross(vu, vr).normalized;
// Compute the screen corner vectors.
Vector3 va = pa - pe;
Vector3 vb = pb - pe;
Vector3 vc = pc - pe;
// Find the distance from the eye to screen plane.
float d = -Vector3.Dot(va, vn);
// Find the extent of the perpendicular projection.
float nd = n / d;
float l = Vector3.Dot(vr, va) * nd;
float r = Vector3.Dot(vr, vb) * nd;
float b = Vector3.Dot(vu, va) * nd;
float t = Vector3.Dot(vu, vc) * nd;
// Load the perpendicular projection.
_camera.projectionMatrix = Matrix4x4.Frustum(l, r, b, t, n, f);
_camera.transform.rotation = Quaternion.LookRotation(-vn, vu);
}
※ 論文と比べると外積を求める方法が若干異なりますが、これはUnityが採用している座標系によるものです。
論文からの変更点
さて、実は今回の実装は、論文のものと比べて少し変更が入っています。
論文では最終的なマトリクス計算まで説明されています。(P, M, Tマトリクス)
論文でのTマトリクスは『カメラがどこにいるか』を示しています。
が、UnityはCGのレンダリングエンジンを持っているので、カメラの位置自体がすでに位置情報を持っています。
そのため、Unityでの実装ではTマトリクスの計算は必要ありません。
次に、Mマトリクスはすべての頂点をビューの前に移動させる行列です。言い換えると、すべての頂点はビューの正面に置かれます。
これが意味するところは、その行列はカメラを回転させることに他なりません。
ということで、これを達成するためにはUnity API(Quaternion.LookRotation)を使ってカメラを回転します。
Quaternion.LookRotationはふたつの引数を取ります。ひとつめはカメラのフォワードベクトル(つまり-vn)です。
そしてふたつめは上方向ベクトル(つまりvn)です。結果として、プレーンに垂直になるためのカメラの回転を求めることができます。
視錐台に入ったオブジェクトの検知
ここからは余談ですが、今回作成した視錐台を用いることで、この歪んだ視錐台でも、その視錐台内に入ったオブジェクトを検知することができます。
それには、Unityが提供してくれているAPIを持ちて以下のように達成することができます。
private void CheckTargets()
{
Plane[] planes = GeometryUtility.CalculateFrustumPlanes(_camera);
foreach (var col in _colliders)
{
col.GetComponent<Renderer>().material.color = Color.white;
if (GeometryUtility.TestPlanesAABB(planes, col.bounds))
{
col.GetComponent<Renderer>().material.color = Color.blue;
}
}
}
結果は以下の通りです。
上記コードで重要なのはGeometryUtility.CalculateFrustumPlanesとGeometryUtility.TestPlanesAABBメソッドです。
これらは、視錐台内に入ったオブジェクトの検知に使われます。
上記動画を観てもらうと分かる通り、歪んだ視錐台でも正常に動作しているのが分かるかと思います。
ズームも行える
n/dがスケールを意味することは前述の通りです。そしてこれに特定のスケールを掛けることで視錐台をスケールさせズーム表現に使うこともできます。
最後に
自分の英語記事を翻訳するという新しい経験をしましたw
今回、この記事を日本語化しようと思った理由は、今のプロジェクトで使ってみて意外と有用だなーと感じたためです。
しかも歪ませた視錐台でも、オブジェクト検知などにそのまま使えるのは面白いですね。
例えば、プレイヤー視点から見える窓の外にオブジェクトが見えたら、みたいなことにも使えるかもしれません。
ただこれ、VRで利用するとカメラの設定が異なるせいなのか分かりませんが、若干見え方がずれることがあります・・。
このあたりについてはどなたか詳細ご存知の人がいたら教えてもらえるとうれしいです;