e.blog

主にUnity/UE周りのことについてまとめていきます

Unityでガウシアンブラーを実装する

C# Unity シェーダ

概要

よく使う＆表現力の高いぼかし処理。

以前にもぼかしを利用したコンテンツを作成したり、記事を書いたりしていましたがちゃんとぼかしだけにフォーカスしたことはなかったので改めて書きたいと思います。

今回のサンプルを動かしたデモ↓

ちなみに以前、ぼかし関連の内容が含まれていたコンテンツ／記事はこんな感じ↓

qiita.com

qiita.com

なお、今回の記事はこちらの記事を参考にさせていただきました。

light11.hatenadiary.com

あとこちらも。

wgld.org

また、今回のサンプルは以下にアップしてあります。

github.com

ガウス関数とは

Wikipediaから引用させてもらうと以下のように説明されています。

ガウス関数（ガウスかんすう、英: Gaussian function）は、


a\ exp\biggl(- \frac{(x - b)^2}{2c^2}\biggr)

の形の初等関数である。なお、 2c^2 のかわりに c^2 とするなど、表し方にはいくつかの変種がある。

ガウシアン関数、あるいは単にガウシアンとも呼ばれる。

また、特徴として以下のようにも説明されています。

特徴

正規分布関数（正規分布の確率密度関数）として知られる

\frac{1}{\sqrt{2 \pi σ}} exp\biggl(- \frac{(x - μ)^2}{2 σ^2}\biggr)

は、ガウス関数の1種である。

ということで、今回話題にするのはこちらの関数です。


y = \frac{1}{\sqrt{2 \pi  σ}} exp\biggl(- \frac{(x - μ)^2}{2 σ^2}\biggr)

ここでの大事な点としては「正規分布関数」ということでしょう。

これもWikipediaから引用させてもらうと、

平均値の付近に集積するようなデータの分布を表した連続的な変数に関する確率分布

と書かれています。
ガウス関数では上記関数の μの値を0にすると、 x = 0を中心とした釣り鐘型のグラフを描きます。
これが、ぼかしを掛ける重み付けとして重宝する点です。
そしてさらに、 σの値を調整することでグラフの形を調整することができるため、ぼかし具合もパラメータのみで設定できるのが利用される理由でしょう。

ちなみにこの関数をdesmosでグラフ化すると以下のようになります。

www.desmos.com

上記グラフは σの値を変化させた結果です。
尖っていたり、平になっていたり、と形が大きく変化しているのが分かるかと思います。

そして今回利用する関数は、定数部分を1にし、中央がx = 0となるよう、 μの値を0とした以下の関数を用います。


y = exp\biggl(- \frac{(x)^2}{2 σ^2}\biggr)

これをグラフにすると以下の形になります。

www.desmos.com

すべてのグラフが1を最大値として色々な形に変化しているのが分かるかと思います。
このグラフの yの値を重みとし、さらに xの値をサンプリング点からの距離として用いることでブラーを実現します。

ブラーの仕組み

さて、ガウス関数を使ってブラーさせることが分かりましたが、これをどう利用するのか。
まずは以下の画像を見てください。

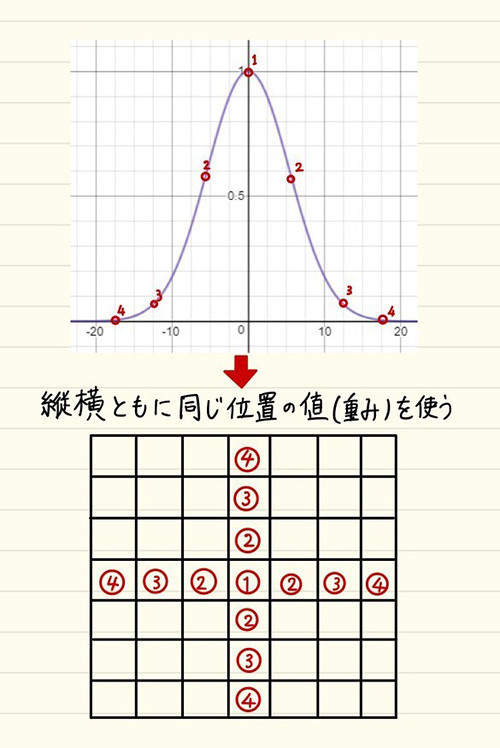
重みの計算

上がガウス関数のグラフの様子、下がテクスチャからテクセルをサンプリングする様子です。
(1)の部分が普通にフェッチするテクスチャの位置を表しています。

そこから(2), (3), (4)が追加でサンプリングするオフセット位置です。
そしてその数字とグラフ上に書かれた数字がそれぞれ、重みとして紐付いた状態を表しています。

つまり、(1)の場合は重み1、(2)の場合はおよそ0.58、という具合です。
中心から離れるにつれて徐々に重みが減っていっているのが分かるかと思います。

ガウス関数を思い出してみると exp\biggl(- \frac{(x - μ)^2}{2 σ^2}\biggr)となっているので、大まかにはexpの値に近いカーブを描くことなるわけです。
（そして引数が x^2を用いているためマイナスが取れて左右対称になっている、というわけですね）

ただし、重みは通常「合計して1になる」必要があるので、最終的な重みは全重みの合計でそれぞれの値を割った値として正規化して利用します。

上下左右は別々に計算できる

概ねブラーの処理についてはイメージできたと思います。
ガウシアンブラーを利用するもうひとつの利点として以下のような性質があります。

wgld.orgの記事から引用させていただくと以下のように記載されています。

さらに、ガウス関数を三次元で用いる場合には x 方向と y 方向を切り離して処理することができます。実はこれが非常に重要です。

どういうことかと言うと、仮に上記のように「切り離して処理することができない」とすると、1テクセルの計算に対しては上の図で言うと、数字の書かれていないテクセルに関してもフェッチして処理しないとなりません。
つまり7 x 7 = 49回のフェッチが必要となります。

しかしこれを分離して考えることができる、という性質から「横方向に7回」、「縦方向に7回」というふうに分けて処理することができることを意味します。
結果、7 x 7 = 49だったフェッチ回数が7 + 7 = 14という回数に劇的に少なくなるわけです。
（そしてこれは、対象とするテクセル数が増えれば増えるほど顕著に差が出てきます）

実際にブラーがかかっていく様子を、Frame Debuggerで出力された画像を見てみると以下のように3回のパスを経て生成されています。

まず、テクスチャをコピーします。（またブラーの性質上、対象画像が縮小されてもあまり問題ないため半分のスケールにしてからコピーしています）

そしてまず、横方向にブラーをかけます↓

さらに横方向ブラーがかかった画像に対して縦にブラーをかけます↓

最終的にしっかりとブラーがかかっているのが分かるかと思います。

シェーダを実装する

仕組みが分かったところでシェーダの実装です。
あまり長いコードではないので全文載せます。

Shader "Custom/BlurEffect"
{
    Properties
    {
        _MainTex("Texture", 2D) = "white" {}
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            ZTest Off
            ZWrite Off
            Cull Back

            CGPROGRAM
            #pragma fragmentoption ARB_precision_hint_fastest
            #pragma vertex vert
            #pragma fragment frag
            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float4 vertex : SV_POSITION;
                half2 uv : TEXCOORD0;
            };

            sampler2D _MainTex;

            half4 _Offsets;

            static const int samplingCount = 10;
            half _Weights[samplingCount];
            
            v2f vert (appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = v.uv;

                return o;
            }
            
            fixed4 frag (v2f i) : SV_Target
            {
                half4 col = 0;

                [unroll]
                for (int j = samplingCount - 1; j > 0; j--)
                {
                    col += tex2D(_MainTex, i.uv - (_Offsets.xy * j)) * _Weights[j];
                }

                [unroll]
                for (int j = 0; j < samplingCount; j++)
                {
                    col += tex2D(_MainTex, i.uv + (_Offsets.xy * j)) * _Weights[j];
                }

                return col;
            }
            ENDCG
        }
    }
}

一番重要なのはフラグメントシェーダでしょう。
samplingCount分だけfor文でループしているのが分かるかと思います。
ふたつループがあるのは、中心から左右（あるいは上下）にテクセルをフェッチするためそれぞれ2回に分けて書いているだけです。

必要となるオフセット位置についてはC#側から設定して計算しています。
また同様に、重みに関してもC#側から渡しています。

理由としては、パラメータが変化しなければ重みに変化がないためアップデートが必要なときだけ計算を行っているためです。

次に、C#の実装を見てみます。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.Rendering;

namespace Sample
{
    public class GaussianBlur : MonoBehaviour
    {
        [SerializeField]
        private Texture _texture;

        [SerializeField]
        private Shader _shader;

        [SerializeField, Range(1f, 10f)]
        private float _offset = 1f;

        [SerializeField, Range(10f, 1000f)]
        private float _blur = 100f;

        private Material _material;

        private Renderer _renderer;

        // Apply sevral blur effect so use as double buffers.
        private RenderTexture _rt1;
        private RenderTexture _rt2;

        private float[] _weights = new float[10];
        private bool _isInitialized = false;

        #region ### MonoBehaviour ###
        private void Awake()
        {
            Initialize();
        }

        private void OnValidate()
        {
            if (!Application.isPlaying)
            {
                return;
            }

            UpdateWeights();

            Blur();
        }
        #endregion ### MonoBehaviour ###

        /// <summary>
        /// Initialize (setup)
        /// </summary>
        private void Initialize()
        {
            if (_isInitialized)
            {
                return;
            }

            _material = new Material(_shader);
            _material.hideFlags = HideFlags.HideAndDontSave;

            // Down scale.
            _rt1 = new RenderTexture(_texture.width / 2, _texture.height / 2, 0, RenderTextureFormat.ARGB32);
            _rt2 = new RenderTexture(_texture.width / 2, _texture.height / 2, 0, RenderTextureFormat.ARGB32);

            _renderer = GetComponent<Renderer>();

            UpdateWeights();

            _isInitialized = true;
        }

        /// <summary>
        /// Do blur to the texture.
        /// </summary>
        public void Blur()
        {
            if (!_isInitialized)
            {
                Initialize();
            }

            Graphics.Blit(_texture, _rt1);

            _material.SetFloatArray("_Weights", _weights);

            float x = _offset / _rt1.width;
            float y = _offset / _rt1.height;

            // for horizontal blur.
            _material.SetVector("_Offsets", new Vector4(x, 0, 0, 0));

            Graphics.Blit(_rt1, _rt2, _material);

            // for vertical blur.
            _material.SetVector("_Offsets", new Vector4(0, y, 0, 0));

            Graphics.Blit(_rt2, _rt1, _material);

            _renderer.material.mainTexture = _rt1;
        }

        /// <summary>
        /// Update waiths by gaussian function.
        /// </summary>
        private void UpdateWeights()
        {
            float total = 0;
            float d = _blur * _blur * 0.001f;

            for (int i = 0; i < _weights.Length; i++)
            {
                // Offset position per x.
                float x = i * 2f;
                float w = Mathf.Exp(-0.5f * (x * x) / d);
                _weights[i] = w;

                if (i > 0)
                {
                    w *= 2.0f;
                }

                total += w;
            }

            for (int i = 0; i < _weights.Length; i++)
            {
                _weights[i] /= total;
            }
        }
    }
}

C#のコードのほうがやや長いですね。
ただ、フィールドの定義以外はそこまで処理は多くありません。

まず、今回の主題である「ガウス関数」での重み付けを更新しているのがUpdateWeightsメソッドです。

private void UpdateWeights()
{
    float total = 0;
    float d = _blur * _blur * 0.001f;

    for (int i = 0; i < _weights.Length; i++)
    {
        // Offset position per x.
        float x = i * 2f;
        float w = Mathf.Exp(-0.5f * (x * x) / d);
        _weights[i] = w;

        if (i > 0)
        {
            w *= 2.0f;
        }

        total += w;
    }

    for (int i = 0; i < _weights.Length; i++)
    {
        _weights[i] /= total;
    }
}

_blurはブラーの強さの係数です。
続くループ処理では各テクセルの重みを計算しています。

xは中心からどれくらい離れているか、を示す値です。まさに関数のxと同義ですね。
ただ、2倍にしているのは入力であるxの値を若干オフセットさせています。（オフセットは値が大きめにばらけるようにしているだけなので、なくても大丈夫です）

そして最後に、求めたそれぞれの重みを、重み全体の合計で割ることで正規化しています。

ブラーのためのダブルバッファ

次に、バッファの準備です。
上で書いたように、縦横それぞれのブラーを適用するためふたつのバッファを用意して処理を行います。
そのため、以下のようにふたつのRenderTexutreを用意します。（と同時に、対象となるテクスチャの半分のサイズにしてダウンスケールしています）

また、ブラーに利用するマテリアルを生成しておきます。

_material = new Material(_shader);
_material.hideFlags = HideFlags.HideAndDontSave;

// Down scale.
_rt1 = new RenderTexture(_texture.width / 2, _texture.height / 2, 0, RenderTextureFormat.ARGB32);
_rt2 = new RenderTexture(_texture.width / 2, _texture.height / 2, 0, RenderTextureFormat.ARGB32);

そして実際にブラー処理を行っているのが以下の箇所です。

public void Blur()
{
    Graphics.Blit(_texture, _rt1);

    _material.SetFloatArray("_Weights", _weights);

    float x = _offset / _rt1.width;
    float y = _offset / _rt1.height;

    // for horizontal blur.
    _material.SetVector("_Offsets", new Vector4(x, 0, 0, 0));

    Graphics.Blit(_rt1, _rt2, _material);

    // for vertical blur.
    _material.SetVector("_Offsets", new Vector4(0, y, 0, 0));

    Graphics.Blit(_rt2, _rt1, _material);

    _renderer.material.mainTexture = _rt1;
}

冒頭でテクスチャのコピーを行い、必要な重みを設定しています。
その後、必要なテクセルフェッチ位置のオフセットを計算し設定しています。

ちなみにここでのオフセットは、シェーダを見てもらうと分かりますが、フェッチするテクセルごとのオフセットです。
つまり、仮にここで2（相当。実際はUV値なので少数になる）を渡したとすると、通常のフェッチ位置を0として、2, 4, 6, 8...と、2テクセル隣のテクセルを、サンプリング回数分飛び飛びにフェッチしていくことになるわけです。

なのでオフセットの値を大きくするとボケをより大きくすることができます。
（ただし、飛び飛びでの処理になるので大きすぎるとブラーというより「ズレ」のような効果になります）

今回実装したブラー処理は以上です。

なお、この処理をCommand Bufferなどを用いて適切なタイミングでキャプチャした映像を用いると以下のような、擦りガラス的な表現を行うこともできます。

これは公式のサンプルで掲載されているものですが、こちらのサンプルではもう少しシンプルなブラー処理になっています。

あるいは場面転換とかで全体にブラーを適用してもいいかもしれませんね。