頂点座標とUV座標から接ベクトルを求める

概要
接ベクトル空間
- 接平面
頂点にある5要素から接ベクトルを求める
- テクスチャ座標のUV値の変化を観察する
- ローカル座標をUV座標で表す
実装コード
パースペクティブコレクト
- パースペクティブコレクトを用いるとき

概要

法線マップを利用する際に使われる「接ベクトル空間」。
今回はその接ベクトルを頂点座標とUV座標から求めるくだりを書いてみます。

先に断っておくと、今回の記事の内容はマルペケさんのこちらの記事（その12 頂点座標とUV座標から接ベクトルを求めるちょっと眠い話）を参考に、Unityで実装したものになります。

なので、今回の記事は上記記事を参考にUnityで実装するにあたって自分の理解をメモするためのものです。

ちなみにUnityで動かすとこんな感じ↓

UV値から接ベクトルを求めるやつ実装してみた pic.twitter.com/MUcO6j7S8u
— edom18@AR / MESON (@edo_m18) 2018年8月22日

今回実装したやつはGithubにアップしてあります。

github.com

今回は接ベクトルについての話のみになります。
バンプマップについては以前、Qiitaの記事で書いているのでそちらをご覧ください。

qiita.com

余談ですが、前回の記事では（法線マップは使っていませんが）バンプマップを使って波紋エフェクトを表示する内容で記事を書いたのでよかったら読んでみてください。

edom18.hateblo.jp

接ベクトル空間

法線マップを利用する上で「接ベクトル空間」の話は外せません。
なぜなら、法線マップの情報はこの接ベクトル空間での値が格納されているからです。

ということで、今回は接ベクトル空間、接ベクトルを求める話です。

接ベクトルはその名の通り、「とある点（ピクセル）に接している」ベクトルのことです。
図にすると以下のような感じ。

f:id:edo_m18:20180827084802p:plain

見てもらうと分かる通り、とある点（ピクセル）の上に乗っている直交座標系と見ることができます。
ただ、「乗せる」と一口に言っても、「どう乗せるか」が問題です。

もちろん座標系をどう取ろうが本来は自由です。
しかし、今回は「法線マップ」の法線を適切に扱うことを目標としているので、自分勝手に定義してしまっては適切な法線を得ることはできません。

そしてこれが今回の主旨である「頂点情報から接ベクトルを求める」になりますが、座標系をどう取ったら適切な法線が取れるのか、を解説していきます。

接平面

接平面とは、今回の接ベクトル空間のUVベクトルが成す平面です。
つまり接ベクトルが成す平面ということですね。

接平面については以下の記事が分かりやすいでしょう。

接平面と接ベクトル - 物理とか

詳細は記事を読んでいただくとして、ざっくりと説明します。

記事を引用すると、

接平面を求めるには、曲面のある点において2つの接ベクトルを求めればいい

ということなのでまずは曲面を表す式を以下のように定義します。

これはふたつのパラメータによって曲面が表されています。
方針としては曲面のある点において2つの接ベクトルを求めるので、この点を含むふたつの曲線を表現しそれの接線を求めることで接平面を求めることにします。

そしてできるだけ分かりやすい曲線を選ぶようにするために、以下のようにふたつの関数を定義してみます。

これは、曲面の定義から媒介変数 $t$ によってパラメータが変化する2つの曲線の関数を取り出したと見ることができます。

さて、この曲線の変化を見ることで接線を求めることができるわけですね。
曲線の変化は微分の出番なので、以下のようにして偏微分で求めます。

頂点にある5要素から接ベクトルを求める

接ベクトルを求めるのに「接平面」を考えることを書きました。
だいぶざっくり書いてしまったので、細かな点については紹介した記事を読んでください。

ここで言いたかったのは、接平面をどう定義し、どうやって必要なベクトルを求めるか、のヒントを得ることです。

さて、話は変わって。
3Dの世界では頂点はポリゴンを形成するひとつの点を表します。
なにを当たり前のことを、と思うかもしれませんが、頂点を表す要素のうち、（x, y, z）要素が頂点の「位置」を決めます。
昔ながらの3Dであれば「頂点カラー」と呼ばれる、頂点ごとに設定された色情報を読み出して処理することもありました。（最近ではカラーとしてそのまま使うケースは稀でしょう）

このように、「頂点ごとに様々な情報」を付与してレンダリングを行うのが3Dです。
そしてテクスチャ空間をあらわす（u, v）値も頂点に付与される情報です。
これはもちろん、テクスチャの位置を決める値です。

つまり、位置を司る情報としては（x, y, z）に加え、（u, v）の合計5要素がある、というわけですね。

そして見出しの通り、この（u, v）値を利用して接ベクトルを求めます。

テクスチャ座標のUV値の変化を観察する

まず、以下の図を見てみてください。

f:id:edo_m18:20180830131534p:plain

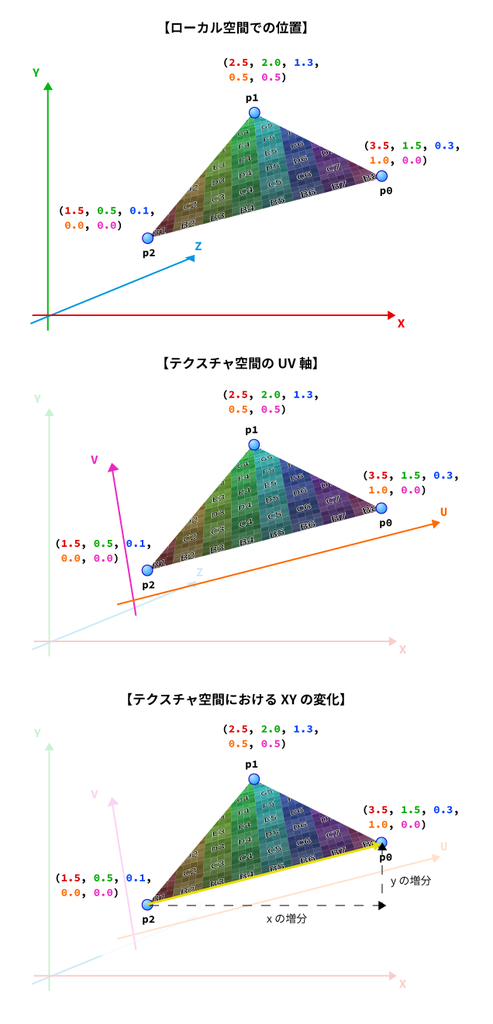
図ではU軸の方向に移動すると（x, y）の値がどう変化するかを示したものです。
（本来は（z）の値も同様に考える必要がありますが、図的に分かりづらいので（x, y）に絞って説明しています）

よくよく見てみると、UVの値の変化の方向はすでに「接平面」に存在していることが分かります。
そしてu方向に移動したとき、xとyの値がどう変化するかを図示したのが上の図です。

u方向に少しだけ移動したとき、xの値がどう変化するのか、あるいはyの値がどう変化するのか。
それぞれの要素に絞って変化を見ているわけです。
これって「偏微分」の考え方ですよね。

そうです。U軸方向への（x, y, z）それぞれの要素の変化量を見ることでU軸の方向ベクトルを得ることができるのです。
これは言ってみれば、UV値の勾配を求めることでそれぞれのベクトルが求まる、ということですね。

そして今回求めたいのは接ベクトル空間の接ベクトルおよび従法線ベクトルです。
これはまさにU軸、V軸ベクトルの方向ですね。

偏微分の記号を使ってU軸およびV軸を表してみると、

と表すことができます。

ローカル座標をUV座標で表す

前述のように位置に関する頂点の情報は全部で5つあります。

ですね。

マルペケさんの記事を引用させていただくと、

ここでうまい事を考えます。5つの成分のうち、例えば(x, u, v)の3成分だけに注目し、3頂点から平面を作ってみます。平面は点の数が3つあればできるわけです。平面の方程式にすると、

$A_0 x + B_0 u + C_0 v + D_0 = 0$

です。両辺を$D_0$で割ると正規化されて、

$A_0 x + B_0 u + C_0 v + 1 = 0$

となります。（ABCの記号が同じ添え字なのは目を瞑ってください(^-^;）。このABCは未知の係数ですが、今頂点が3つあるので解く事ができます。連立方程式を立てても良いのですが、平面の方程式の(A,B,C)は平面の法線である事を利用すると、ポリゴンの法線から一発で求まります。

とのこと。

さて、上記の式を整理すると以下のようになります。

$x$ についての式に変形したわけですね。
さて、これを $u$ について偏微分してみます。すると以下のようになります。

お。これは先に書いた偏微分の $x$ 要素じゃないですか。
そう、この値を導き出すために上記のように平面の方程式を持ち出したのですね。

なお、引用した文章でも示されている通り、この $ABC$ は平面の方程式の意味から「法線ベクトルの各要素（ $x, y, z$ ）」です。
そして平面の法線は3頂点からベクトルを作り、その外積によって求めることができます。

ちなみに平面の方程式についてはこちらを参照↓

mathtrain.jp

そしてU軸およびV軸のベクトルの各要素は、上の例を（y, z）にも適用してやることで以下のように求まります。

さぁ、これを元に実際のコードに落とし込むと以下のようになります。

実装コード

今回はUnityで実装したのでC#コードです。

static public Vector3[] GetTangentSpaceVectors(Vector3[] p, Vector2[] uv)
{
    Vector3[] cp0 = new[]
    {
        new Vector3(p[0].x, uv[0].x, uv[0].y),
        new Vector3(p[0].y, uv[0].x, uv[0].y),
        new Vector3(p[0].z, uv[0].x, uv[0].y),
    };

    Vector3[] cp1 = new[]
    {
        new Vector3(p[1].x, uv[1].x, uv[1].y),
        new Vector3(p[1].y, uv[1].x, uv[1].y),
        new Vector3(p[1].z, uv[1].x, uv[1].y),
    };

    Vector3[] cp2 = new[]
    {
        new Vector3(p[2].x, uv[2].x, uv[2].y),
        new Vector3(p[2].y, uv[2].x, uv[2].y),
        new Vector3(p[2].z, uv[2].x, uv[2].y),
    };

    Vector3 u = Vector3.zero;
    Vector3 v = Vector3.zero;

    for (int i = 0; i < 3; i++)
    {
        Vector3 v1 = cp1[i] - cp0[i];
        Vector3 v2 = cp2[i] - cp0[i];
        Vector3 ABC = Vector3.Cross(v1, v2).normalized;

        if (ABC.x == 0)
        {
            Debug.LogWarning("ポリゴンかUV上のポリゴンが縮退しています");
            return new[] { Vector3.zero, Vector3.zero };
        }

        u[i] = -(ABC.y / ABC.x);
        v[i] = -(ABC.z / ABC.x);
    }

    u.Normalize();
    v.Normalize();

    return new[] { u, v };
}

やっていることは前述の文章の説明をそのままプログラムしただけです。
それぞれのベクトルの外積を取って $ABC$ を求め、そこからUV軸のベクトル要素としているのが分かるかと思います。

以上で接ベクトルを求めることができました。
もしバンプマップなどの計算に用いたい場合は、この接ベクトル空間へライトなどの位置を変換してやり、そこでのシェーディングを計算することで法線マップを利用したライティングが可能になる、というわけです。

パースペクティブコレクト

さて、最後は少しだけ余談です。

今回の色々を実装する際に初めて聞いた単語。

以下の記事に詳しく書かれていました。

ラスタライザを作る人の古文書集 - ushiroad

どういうものかざっくり書くと。

通常、3DCGで画面にレンダリングを行う際は頂点情報を入力しそれをいくつかの座標変換を経て、最終的にスクリーンに表示します。
そしてこのとき、ポリゴンに指定された値（色とUV値など）はSlopeとSpanという処理を行い補間します。

冒頭の記事から引用させていただくと、

ポリゴンを描画するとき、頂点の属性（典型的には色、UV座標）を滑らかに変化させながら各ピクセルを描きます。このとき、頂点の属性を頂点間を結ぶ辺上で内挿したもの（属性値の"坂"）はSlopeと呼ばれます。さらに、2本のSlopeの間にSpan（橋）を架け、この両端の値を内挿することにより、三角形内部の全ての点で内挿値を得ることができます。

ということ。
この補間処理の際、UV値を色などと同じ方法で補間してしまうと問題が生じる、ということのようです。
紹介した記事にはどんな感じになるのかの画像があるので見てみてください。

さて、ではどういうふうに補間処理をしたらいいのかというと。
これも冒頭の記事に解説があります。引用させていただくと、

パースペクティブコレクトの具体的な方法ですが、テクスチャ座標(u, v)をそのまま補間するのではなく、透視変換で出てくる斉次のwを使い

(u/w, v/w, 1/w) という値を頂点毎に作り、これでSlope/Spanの処理を行います。補間結果を

{ (u/w)' , (v/w)' , (1/w)' } としたら、(u/w)' および (v/w)' を (1/w)' で割ります（つまり、補間前にwの逆数をとり、補間後にもう一度wをひっくり返します）

自分の理解を書くと、射影変換された空間で補間処理を行い、かつ1/wも同様に補間しておく。そして補間後の値（(u/w)', (v/w)'）を、補間した(1/w)'で元に戻すことで正常な値が得られる、ということのようです。
（射影空間上で補完処理をして戻す、ということかもしれません）